基于航空公司成本最小化的飞机排班问题模型与算法

吴东华, 夏洪山

(南京航空航天大学 a.继续教育学院;b.民航学院,南京 210016)

定义2对每个最优值Z*l,(l=1,2,…,6),

基于航空公司成本最小化的飞机排班问题模型与算法

吴东华a,b, 夏洪山*b

(南京航空航天大学 a.继续教育学院;b.民航学院,南京 210016)

针对影响航空公司运营成本的四个关键因素,在满足航班衔接、航班覆盖和机队规模约束条件下,以最小化运营成本、最小地面等待时间、最小总飞行时间绝对偏差和最少起降次数为目标函数,建立了飞机排班问题的 0-1 整数模糊线性规划数学模型.基于东方航空公司实际数据,应用模糊线性规划理论对模型进行验证,表明该模型可行,算法有效.

航空运输;飞机排班;多目标优化;计算机仿真;东方航空公司

1 引 言

飞机排班问题是多目标多约束条件的组合优化问题,是民航界著名的 NP 难题.合理的飞机排班不仅有助于航班的安全、正点运行,而且还能够提高机队的利用率,有效地降低运营和维护成本.航空公司优化飞机排班问题的目的是增加旅客运输、货运运输等方面的收入,降低航空公司的运营成本,综合考虑机队飞行的经济效益和社会影响.

国外大多数航空公司的航线网络都是各种形态的枢纽轮辐式(hub-and-spoke) 结构,在各枢纽之间及轮辐城市之间有很高的航班频次,每天的航班计划基本相同,而且其限制飞机排班的一个最重要约束是“4 天维护规则”.而在我国,航空公司的运营主要是基于点到点的单枢纽模式,一周内各天的航班计划有较大的差异,飞机排班时需考虑的约束较多,因此国外现有的研究结果并不适用于我国,必须找到一种切实可行、适应我国航空公司运营的方式.国内研究飞机排班问题有:孙宏等人应用模拟退火算法、二部图最大匹配方法和固定工件排序模型及 Hungarian 算法研究了基于最少飞机数、飞机使用均衡和满足飞机调度指令的飞机排班问题,并在其《飞机排班数学规划模型》中,对 20架飞机,35 个航班应用上述算法得到一个满意的排班方案时间接近 23 秒[1].王伟、王锦彪从划分与划分加细的角度讨论了航班组合等问题[2].近年来,高强[3]等设计了一种基于约束编程思想的列生成算法,将机型指派、路线选择与机尾号指派综合考虑,构建了飞机排班的整数规划与约束规划杂交一体化模型.魏星等人[4]在其基础上提出了一种加入航班经停并以星期为排班周期的综合排班新方法.廖峰等[5]应用图着色理论,根据" 先到先服务"的原则给出了飞机分配的顶点序列着色算法.朱星辉等人[6]把飞机排班问题构建为多商品网络流模型,并应用列生成算法求解.国外相关研究有:Clarke 等人[7]将飞机路线问题转换为带有边约束的旅行商问题(TSP),并利用 Lagrangian 松弛算法求解;Papadakos[8]建立了航班计划的多个综合优化模型,并在 Bender's 分解及列生成法的子问题中应用启发式方法加速求解过程. Mattias[9,10]建立了基于列生成法的飞机排班的约束编程模型,并用约束传播加速列的生成.

上述算法均为民航飞机排班问题的解决提供了思路,然而,已有算法均不能有效解决飞机排班过程中的多目标优化问题,没有从根本上提高航空公司的经济效益.本文结合航空公司实际运营管理情况,通过分析国内航空公司运营成本的构成,针对影响其收益的四个关键要素,借鉴已有模型的合理性,建立了飞机排班问题的 0-1 整数线性规划模型,并应用模糊数学理论对该模型进行了求解.

2 飞机排班问题的数学建模

为了从根本上提高航空公司效益,需要在影响航空公司收益的诸多要素中找到关键要素.飞机排班问题的数学模型将在满足航班衔接、航班覆盖与机队规模的基本运行约束条件下,以这些关键要素为优化目标.

2.1 航空公司收益与运营成本分析

《从统计看民航》[11]中的数据显示了近年来我国民航企业业务收入的状况(见表1).从表中我们发现,我国民航企业业务收入在逐年增加,其中国内航线收入一直高于国际及地区航线运输收入,几乎是其两倍.而航空公司的客运和货运运输收益却高于通用航空收入、机场服务收入与其他收入总和,大约占总收入的 60%.因此,既然飞机是一种昂贵的设备,那只有保证每天一定数量的飞行时间,尽量提高飞机的日利用率,才能最大限度地保证航空运输收入的增加,从而提高经济效益.

表1 2005-2008 年民航企业业务收入 (单位:万元) ________Table1 Operation revenue of civil aviation enterprises from 2005 to 2008(unit:ten thousand yuan)

从成本上来说,国内航空公司的运营成本通常包括飞行运营成本(也称直接运营成本 DOC)和非直接运营成本( 也称间接运营成本) 两部分[12],其具体内容及相应影响因素、所占比例如表2所示.

表2 航空公司运营成本构成Table2 The construction of the airline operation cost

从表2可以看出,虽然飞行运营成本和非直接运营成本占总运营成本的比例相当,但在飞行运营成本中有更多可以进一步优化的部分,比如:直接飞行成本和飞机维修成本两项就占飞行运营成本的 3/4 之多,占总运营成本的 40%.通过表2 还可以看出,影响直接飞行成本的因素主要有飞机日利用率、航段耗油量及国际油料价格.其中的国际油料价格在一定时间内是相对稳定的,模型中可以使用一个常量替代之.航段耗油量与飞机任务航段里程是成正比关系的,飞行里程长,航段耗油量自然就大些.另外,由于只有尽量提高飞机的运输能力,才能最大限度地保证航空客货运输收入的增加,所以,提高飞机日利用率显然是关键因素之一.而减少飞机的地面等待时间可以为飞机在空中飞行争取更多的时间,为提高飞机日利用率提供保证.

影响飞机维修成本的因素主要是飞机的使用年限及民航总局规定的定期维护.为了保证飞机有更长的服务时间,避免飞机的忙闲不均带来高的机队维修成本,模型需要考虑飞机使用上的均衡,这包括每架飞机每日飞行时间上的均衡与航班起降班次的均衡.

占非直接运营成本中比例最多的是地面运营成本(59.6%),约占总运营成本的 28%.在影响地面运营成本的因素中,可以进行优化的是与起降相关的飞机地面成本.按照规定,不同最大业务载重量和不同座位数的飞机在各个类型的航站需要支付不同的起降费和旅客服务费.

2.2 飞机排班问题的数学模型

航空公司在进行飞机排班时需要考虑如何合理调度机队中的每架飞机,完成所有给定航线的不同航班,在降低运营成本的同时实现经济和社会效益.模型的建立将以降低航段燃油量与起降费、旅客服务费等飞机运营成本,实现飞机飞行时间平衡、飞机起降次数均衡,以及降低飞机地面等待时间为优化目标.

定义决策变量为

式中 可行航班环 j∈ R(可行航班环集合).可行航班环集合是为了首先满足航班衔接的要求,预先根据航班计划,将当天飞行任务中能满足航班衔接要求的各航段串行连接起来,组成了可行航班环,多个可行航班环组成可行航班环集合 R.根据决策变量的定义可知,每一个可行航班环对应一架飞机当天的全部飞行任务.

2.2.1 目标函数

由于不同可行航班环的实际飞行时间不同,令航班环 j的飞行时间为 Tj(小时),飞机的单位小时油耗为 c(吨), 设:飞机的轮档时间=1.2·飞行时间=1.2· Tj,每吨油料价格为 b(元),则航班环 j的航油成本为 c·(1.2·Tj)·b.在 1 天中, 所有航班的航油成本 C1为

令:可行航班环 j所停靠航站的使用费(包括起降费、安检费和旅客服务费)为 nj,则飞机在航班环 j上所停靠航站的经停费 C2为

因此,飞机排班问题的成本目标 Z1为

令:1 天内,每架飞机的平均飞行时间为 ～Q,其中 , ～Q 为 L-R 型 模糊 数 ,记 为 : ～Q=(Q;).考虑飞机的飞行时间均衡,最小化所有飞机飞行时间与 ～Q 的总绝对偏差,目标 Z2为

令:可行航班环 j上飞机起降次数为 Pj,设航班集合 F 的模为 M,机队规模为 V,那么,1 天内,一架飞机平均起降次数最小化所有航班班次与平均起降次数 N 的总绝对偏差,目标 Z5为

飞机过站时间是指从航空器滑至停机位开启机门至航空器准备工作就绪关闭机门之间的时间.按照规定,飞机在地面进行航班衔接的时间,不得少于最少过站时间.由于只有尽可能地缩短衔接航班间的地面等待时间,才能为提高飞机日利用率提供可能.因此,令:可行航班环 j中衔接航班间的等待时间为 wj,最少过站时间为 tj,将最小化可行航班环中衔接航班间的等待时间总和作为目标Z6

2.2.2 约束条件

令:航班号 i,i∈ F(航班集合);定义参数ai,j为

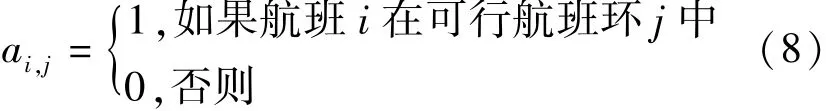
飞机排班问题的多目标 0-1 整数规划数学模型中的三个约束条件为

式(9)表示航班覆盖的约束,即每个航班只能由一架飞机值飞[13],并且所有飞行任务只能覆盖航班当且仅当一次;式(10)表示机队规模要求,即所使用的飞机数量不能超出公司所拥有的机队总量;式(11)是决策变量的 0-1 整数性要求.

3 模型求解算法研究

求解目标函数系数带有 L-R 型模糊数的多目 标 模 糊 线 性 规 划 问 题 的 方 法 是: 先 根 据 ～max的近似公式,将带有 L-R 型模糊系数的目标函数近似等价于一个具有三个目标的线性规划问题,然后将线性规划中的各个目标函数模糊化,引入隶属度函数,从而导出一个新的线性规划问题,新问题的最优解成为原问题的模糊最优解[14].针对多目标飞机排班问题线性规划模型,在求解时除了要考虑目标函数中有带 L-R 型模糊数系数的目标如何转化的问题,同时还要采用折中的方法来处理多个目标函数,以使各目标相对地“极大”,这主要是因为,要想使多个目标函数均达到最优解往往是困难的.

3.1 带 L-R 型模糊系数的目标函数的近似等价

首先解决目标函数带模糊数系数的问题.在目标函数 Z2中包含 L-R 型模糊数 ~Q,按照 L-R 型

至此,由于将带 L-R 型模糊系数的目标函数进行了近似等价,飞机排班问题数学模型中的目标函数由原来的 Z1,Z2,Z5与 Z6,变成了目前的 6 个目标函数,它们分别是 Z1,Z2,Z3,Z4,Z5,Z6,即式(4),式(12),式(13),式(14),式(6),式(7).

3.2 多目标线性规划问题的模糊求解算法

令:在式(9)、式(10)、式(11)约束下求解各单目标函数 Zl(l=1,2,…,6) 的最优值为 Z*l.定义 1定义 Zkl(k=1,2,…,6) 为:定义能反映各目标重要性程度的伸缩性指标 dl(dl＞ 0)为其中 dl(l=1,2,…,6) 越小,表示目标函数 Zl越重要.

定义2对每个最优值Z*l,(l=1,2,…,6),

定义 3设:各目标函数下的系数为 clj,定义多目标隶属度函数 Fl(x),(l=1,2,…,6) 为

根据定义 3 可知,Fl(x) 越接近于 1,表示 x 属于 Fl的程度越高;Fl(x) 越接近于 0,表示 x 属于Fl的程度越低. 因此,隶属度函数 Fl(x) ∈ [0, 1](i=1,2,...,6) 可以表征 x 属于 Fl的程度高低.通过引入隶属函数 Fl(x),可以将线性规划中的多个目标函数模糊化.

定义4令:则 F 是对应于多目标函数 Z=Cx模糊化后的模糊目标集,λ是x属于F的隶属度.

按照定义4中对 F 和 λ 的定义,目标函数带L -R型模糊系数的飞机排班问题的多目标模糊线性规划模型可以转化成单目标 0-1 整数线性规划模型式(19).

综上所述,求解飞机排班问题的算法步骤如下:

Step1将式(4) 、式(5)、式(6)、式(7) 中求min 的目标函数化成求 max 的目标.

Step2按照的近似公式,将目标函数 Z2近似等价地化为式(12)、式(13)、式(14)的目标函数.飞机排班问题数学模型的6个目标函数分别为式(4)、式(12)、式(13)、式(14)、式(6)、式(7).

Step3在式(9) 、式(10)、式(11) 约束下求解各单目标函数 Zl(l=1,2,…,6) ≥ 的最优值为Z*.按照式(15) 计算 Z(k=1,2…,6).

Step4按照式(16) 计算伸缩性指标 dl.其中,l=1,2,…,6.

Step5对式(4) 、式(12) 、式(13) 、式(14)、式(6)、式(7)中每一个目标函数,按照式(17)选取隶属度函数 Fl(x).

Step6按照公式(18)中的定义,求解数学模型式(19),得到 λ 的最大值,记为 λ*.其中,0-1整数化最优解,记为 x*.

Step7将 x*分别代入飞机排班问题的各个目标函数式(4)、式(5)、式(6)、式(7),即可获得飞机排班问题的最优解.

4 仿真实验与分析

以中国东方航空公司飞机排班问题为例,根据多目标优化模型及模糊线性规划求解算法进行优化调度.该公司每日有从无锡、南京和浦东机场作为维修基地的 68 个国内航班,需要由 12 架飞机进行值飞.由于篇幅的关系,航班集合 F 的一部分在表3中显示.

表3 部分航班时刻表Table3 Part of the flight schedule

根据航班计划表,遵照民航总局相关规定,搜索到能从维修基地出发,在完成当天任务后返回到维修基地,满足航班衔接条件的共 233 个可行航班环,部分可行航班环见表4.其中,每个可行航班环是由航班计划中的航班按序连接而成,并且满足飞机当天总飞行时间≤14 h;航班间最少过站时间≥45 min.

表4 部分航班环Table4 Part of flight-loop

部分可行航班环的航班间等待时间 wj、飞行时间 Tj、航班环包含的起降次数 Pj显示在表5中.

表5 部分航班环的 wj,Tj,pj值Table5 The values of wj,Tj,pjin the flight-loop

4.1 飞机排班结果对比

一直以来,12架 A320飞机是按表6 所示的方案进行排班的.从表6可以看出,第 5 架飞机是最繁忙的,因为它需要值飞 8 个航班,根据航班序号,我们发现它的飞行路线为:南京-南昌-贵阳-南昌-南京-大连-哈尔滨-大连-南京.而第 1、2、3、4 与9、10、11、12 架飞机需要值飞 6 个航班,第 6、7、8架飞机需值飞4个航班.

按照算法重新优化后的排班结果如表7显示.对比表6与表7两个方案,很容易发现第 1、2、3、4、5、8、9 架飞机的排班方案没有发生变化,而第 6、7、10、11、12 共 5 架飞机的排班却有很大的变化.例如:在表6 中,第 6 架飞机在完成6-19(南京-香港-南京)后衔接 32 号航班和 49 号航班(南京-香港-南京),当天一共值飞 4 个航班,也就是说该飞机当天的飞行任务就是完成两次的南京到香港往返飞行;而表7中新的方案却要求该飞机在值飞完一次南京-香港往返之后衔接 31 和 45 号航班,并且飞行完 45 号航班后,还要继续值飞 56 和 65 号航班,即接下来要飞往长沙、昆明、武汉,最后降落在无锡机场.这样,这架飞机当天要比原来多值飞两个航班.同样的状况也发生在第 7 架飞机上,原来只需值飞 7-18-36-53(南京-西安-乌鲁木齐-西安-南京)4 个航班,现在却要增加飞行 63-68 (南京-张家界-南京)2 个航班.

表6 原有飞机排班方案Table6 Original fleet assignment scheme

表7 优化后的飞机排班方案Table7 Optimized fleet assignment scheme

从各架飞机值飞的航班次数、飞行时间,以及地面等待时间方面对比优化前后两种方案,结果如表8所示.

表8 优化前后飞机排班方案对比Table8 Comparison of fleet assignment schemes

4.2 性能对比

优化前后的四个性能指标值分别如表9所示.

表9 优化前后性能指标对比Table9 Comparison of performance index

和优化前相比较,我们发现优化后只有飞机飞行时间的总绝对偏差略高于原方案,其他指标均有明显改善,例如:飞行成本下降了 4.85%;飞机当日平均飞行小时为 9.99 h,比统计数据平均日飞行小时 9.79[11]提高 2%;地面等待时间总和为 810 min,与原方案的 945 min 相比,下降了 14. 3%;起降次数的总绝对偏差仍旧为 10,与原方案一致,说明新方法仍旧能保证飞机起降次数均衡.对比结果表明,该飞机排班数学模型可行,算法有效.

5 研究结论

本文通过分析航空公司运营规划与管理中收入与成本构成,提炼出影响航空公司收益的四大关键因素,将地面等待时间最少、飞机使用均衡和航班起降次数均衡因素纳入调度问题,以降低飞行成本、提高飞机日利用率为优化目标,提出了飞机排班问题的多目标0-1 整数规划数学模型.

在解决飞机排班问题时,为了同时满足航班覆盖与航班衔接两个约束条件,本文采用的手段是:预先按照图的深度优先搜索算法将那些能同时满足最小过站时间和航班衔接要求的航班依次连接起来,生成可行航班环,组成可行航班环集合,并在可行航班环集合上定义决策变量.

本文将模糊数学与运筹学理论应用到求解该飞机排班问题上,给出了目标函数带模糊系数的多目标模糊线性规划数学模型的求解算法.最后通过一个飞机排班问题实例.优化前后结果对比表明,该数学模型可行,算法有效.如何进一步优化飞机排班问题,提高飞机的日利用率将是进一步努力的方向.

[1] 孙宏.航空公司飞机排班问题:模型及算法研究[D]. 西 南 交 通 大 学,2003.[SUN H.Airline tail number assignment problem:model and algorithm [D].Southwest Jiaotong University,2003.]

[2] 王伟,王锦彪.中国民航飞机排班问题的多部图模型[J].交通与计算机,2008(04):35-41.[WANG W,WANG J B.A multipartite graph model for aircraft arrangement of CAAC[J].Transport and Computer, 2008(04):35-41.]

[3] 高强, 朱星辉,李云,等.飞机排班一体化模型与算法研究[J].武汉理工大学学报(交通科学与工程版),2012(02):153-157.[GAO Q,ZHU X H,LI Y,et al.Research on integration model and algorithm of airline schedule[J].Journal of Wuhan University of Technology(Transportation Science&Engineering), 2012(02):153-157.]

[4] 魏星,朱金福.航空公司一体化飞机排班研究 [J].武汉理工大学学报(信息与管理工程版),2013 (02):86-90.[WEI X,ZHU J F.Integrated research of airlines aircraft scheduling[J].Journal of Wuhan University of Technology(Information&management Engineering),2013(02):86-90.]

[5] 朱星辉,朱金福,高强.基于约束编程的飞机排班问题研究[J].交通运输系统工程与信息,2011,(6): 151-156.[ZHU X H,ZHU J F,GAO Q.Aircraft scheduling based on constraint programming[J]. Journal of Transportation Systems Engineering and Information Technology,2011,11(6):151-156.][6] 廖峰,刘红,文军. 基于图着色模型飞机智能化排班算法的研究[J].中国民航飞行学院学报,2012(3): 20-23.[LIAO F,LIU H,WEN J.Study on aircraft intelligent assignmentofairlinersbased on graph coloring model[J].Journal of Civil Aviation Flight University of China,2012(3):20-23.]

[7] L W Clarke,E L Johnson,G L Nemhauser,et al.The aircraft rotation problem[J].Annals of Operations Research,1997,69(1):33-46.

[8] N Papadakos.Integrated airline scheduling[J].Computers &Operations Research.2009,36(1):176-195.

[9] G Mattias.The tail assignment problem[D].Goteborg: Department of Computer Science and Engineering, Chalmers University ofTechnology and Goteborg University,2005.

[10] G Mattias.Accelerating column generation for aircraft scheduling using constraint propagation[J].Computers

[8] 刘明俊,艾万政,程志友. 苏通大桥桥区水域船舶通航能力研究[J]. 船海工程,2006(4):80-85.[LIU M J,AI W Z,CHENG Z Y.Research of navigating capacity in the area nearby Sutong bridge[J].Journal of Ship&Ocean Engineering,2006(4):80-85.]

[9] Olsen N R B,Melaaen M C.Three-dimensional calculation of scour around cylinders[J].Journal of Hydraulic Engineering,1993,119(9):1048-1054.

[10] Raudkivi A J.Functional trends of scour at bridge piers[J].Journal of Hydraulic Engineering,ASCE, 1986,112(1):l-12.

[11] YANG Yong-quan,ZHAO Hai-heng.Numerical simulation of turbulent flows passed through an orifice energy dissipator within a flood discharge tunnel[J].Journal of Hydrodynamics,Ser.B,1992,4(3):27-33.

[12] Liu Xiao-bing,Zeng Yong-zhong.Numerical prediction of vortex flow in hydraulic turbine draft tube for LES [J].Journal of Hydrodynamics,Ser.B,2005,17 (4):448-454. &Operations Research.2006,33(1):2918-2934.

[11] 中国民用航空总局规划发展司.从统计看民航[M].北京:中国 民 航 出 版 社,2009:187.[Statistical Data on Civil Aviation of China[M].Beijing:China Civil aviation Press,2009:187.]

[12] 耿淑香.航空公司运营管理方略[M].北京:中国民航出 版 社,2000:34.[GENG S X.Airline operation strategy[M].Beijing:China Civil Aviation Press, 2000:34.]

[13] MASSOUDB.Airline operations and scheduling[M]. BurLin-gton: Ashgate Publishing Limited,2010: 71-122.]

[14] 张振良.模糊集理论与方法[M]. 武汉:武汉大学出版社,2010:227-235.[ZHANG Z L.Fuzzy set theory and its method[M].Wuhan:Wuhan University Press, 2010:227-235.]

Model and Algorithm for Fleet Assignment Problem Based on Airlines Cost Minimization

WU Dong-huaa,b,XIA Hong-shanb
(a.College of Continuing and Education;b.College of Civil Aviation, Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

Aiming at fleet assignment problem,on the basis of flight connecting,flight covering and fleet scale.The objective functions are taken with the minimum variable cost on fleet,the minimum time on ground-holding,the absolute minimum deviation of total flight time and the minimum frequency of taking off and landing.And a 0-1 integer programming mathematical model is established.The historical data of Chinese Orient Airlines Company are analyzed;fuzzy theory are used to demonstrate the model.The result shows that the proposed model is feasible and effective.

air transportation;fleet assignment problem;multi-objective optimization;computer simulation;China Eastern

1009-6744(2014)01-0109-08

TP391.41

A

2013-07-16

2013-10-08录用日期:2013-10-28

国家自然科学基金项目(60672167);国家软科学研究计划项目(2008GXQ6B141).

吴东华(1973-),女,黑龙江佳木斯人, 讲师, 工学博士生.*通讯作者:xhsca@nuaa.edu.cn