基于多维离散粒子群优化的协同OFDMA系统跨层资源分配
李为,熊春林,王德刚,张晓瀛,魏急波
(国防科学技术大学 电子科学与工程学院,湖南 长沙 410073)
1 引言
OFDMA(orthogonal frequency division multiple access)技术具有较高的频谱利用效率和对抗多径衰落的优良特性,被普遍认为是当前和未来移动通信网的关键传输技术之一。协同中继技术能显著增加通信网络的覆盖范围和链路的可靠性,具有广泛应用前景。基于中继协同的OFDMA系统可充分结合2种技术的优点,已经引起了国内外学者们和业界的研究兴趣,并被IEEE 802.16j和3GPP-LTE 等多个标准组织采纳。
资源分配能显著提高协同OFDMA系统的频谱效率和多用户分集增益。协同OFDMA系统的资源分配主要包括中继选择、子载波分配和功率分配。目前,已有的工作大部分目标为保证一定公平性的约束条件下最大化系统的吞吐量[1,2]。此类方法倾向于将更多资源分配给信道条件较好的用户,而位于较差信道条件下的用户往往得不到足够的资源。文献[3, 4]针对公平性问题,采用比例速率约束和最大最小公平性准则来改善公平性,但是又引入了新的问题,信道环境很差的用户会占用大量的系统资源,导致整个系统的吞吐量降低。
为了实现公平性和吞吐量的更优折中,人们引入效用(utility)理论来衡量网络中用户的满意程度[5~7]。效用的高低取决于用户的应用层需求。文献[6]研究了协同OFDMA系统中基于效用最大化的资源分配问题,但是只考虑基站和协同节点总功率约束(TPC,total power constraint)的条件。实际场景往往需要考虑基站和中继单独功率约束(PPC, per-relay power constraint)的情况,该约束条件下的资源分配问题更为复杂。
本文以所有用户的总效用最大为优化目标,研究PPC 约束条件下的协同OFDMA跨层资源分配问题。和以往的研究不同的是,本文考虑多服务的协同OFDMA系统,且每个用户根据应用层的需求具有自己独立的效用函数,这更符合实际情况。这样,资源分配成为一个离散和连续变量混合的多维优化问题,这是一个NP 问题。文献[1]研究了TPC条件下加权速率最大化资源分配问题,采用的方法是将离散变量松弛为连续变量,将问题转化为凸优化问题用对偶法来求解。但是,多服务情况下,用户的效用函数存在多样性,甚至可能是不连续函数,很难将资源分配问题转化为凸优化问题来求解。
在解析类方法遇到困难时,启发式智能算法提供了一条有效解决问题的思路,如粒子群优化(PSO,particle swarm optimization)算法。PSO算法是一种基于群体智能的统计最优化算法,由Eberhart和Kennedy受到鸟群捕食的启发在1995年提出[8,9],能够高效求解高度非线性的混合优化问题,因此在工程中得到广泛应用[10~12]。PSO算法最初用来求解连续变量的优化问题,现在已有文献针对离散粒子群算法进行了研究,并将其应用到了离散优化问题中[13~15]。然而,这些方法仅仅将连续空间上的运算法则简单搬移到离散空间中,没有考虑离散空间的特点。为了更好地提高离散空间的搜索效率,需要根据离散空间的特点建立起特殊的运算法则。
为解决多服务协同OFDMA系统的资源优化问题,本文提出了一种多值离散粒子群优化(MDPSO,multi-values discrete particle swarm optimization)算法。所提算法根据多维离散空间的特点,构建了新的基于概率特性的运算法则,由此建立了粒子速度和位置的更新策略。所提MDPSO算法可以广泛用于求解各类高维组合优化问题。仿真结果显示本方法很好的解决了资源优化问题,效用和公平性2个指标相对于目前已有算法均取得了较大的性能提升。
2 系统模型和问题阐述
2.1 协同OFDMA系统模型
如图1所示,所考虑的协同OFDMA系统具有1个基站(BS, base station),K个中继站(RS, relay station),和M个移动站(MS, mobile station)。系统可供使用的子载波数目为N,总带宽为W,每个子载波的带宽为W/N。BS和 MS m、BS和RS k、RS k 和 MS在子载波n上的信道系数分别表示为每个子载波上的噪声为0均值循环对称复高斯变量,方差为N0W/N。

图1 协同OFDMA系统模型
考虑2种类型的中继策略:放大转发(AF,amplify-and-forward)和译码转发(DF, decode-andforward)。设定每个子载波在同一时刻最多分配给一个用户和一个中继(没有子载波复用)。中继的处理过程如下:首先,基站(BS)在子载波n上以功率发送信号给中继节点(RS)和移动站(MS),然后,RS k接收到信号后在相同的子载波上以功率译码转发或者放大转发给MS m。由文献[16]得到中继用户对(RS k, MS m)在子载波n上的信道容量为

其中,
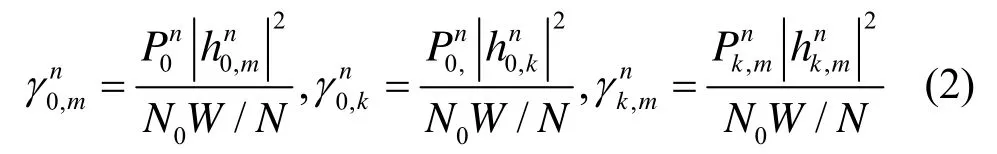
为了表示方便,将中继选择方法和子载波分配方案用2进制变量表示。表示子载波n和中继K分配给用户m,否则,
这样用户m 的容量可以表示为


图2 BE服务效用函数(C=90 kbit/s)
2.2 效用函数
用户满意的程度可以用效用来表示,效用是用户速率的函数。采用效用函数进行跨层优化设计可以很好地获得效用和公平性的平衡。针对不同的服务和不同的用户,会有不同的效用函数[17]。本文考虑了2种服务类型:最大努力服务(BE)和速率约束服务(RC)。
最大努力服务(BE)的效用函数可以表示为[18]

速率约束服务(RC)的效用函数可以表示为

其中,minR表示用户最低的速率需求。
针对不同的MS 参数ma或minR可能具有不同的取值。根据用户的不同需求还可以设置其他效用函数。
2.3 问题阐述
本文资源优化的目标是最大化用户的效用总和。优化问题表示为如下。
Problem: P1
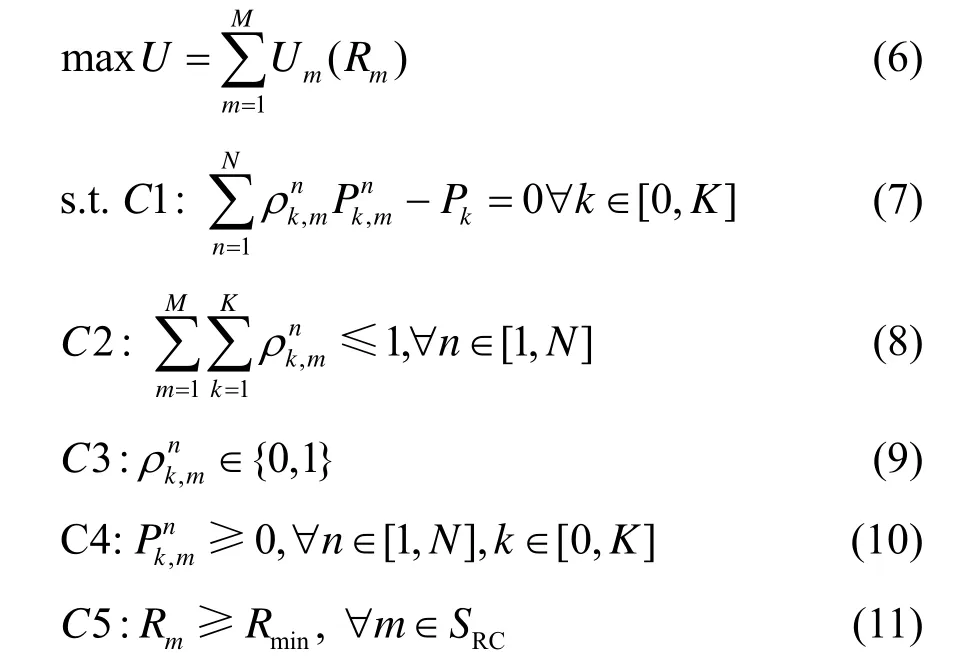
其中,kP表示基站(k=0)或者中继站(k=1, 2,…, K)的最大发送功率;式(7)为基站和中继站的功率约束;式(8)和式(9)保证了每个子载波最多分配给一个用户和中继站;式(11)保证RC 用户的需求,RCS表示RC用户的集合。明显问题P1为带有非线性约束条件的连续和离散变量混合优化问题,为NP-hard问题。在下一节中将采用MDPSO算法来求解。
3 资源分配算法
前一节定义的资源优化问题,为离散和连续混合变量优化问题。采取分而治之的办法,将问题P1分为2个子问题:子载波中继分配和功率分配。首先采用均匀功率分配方案,在此前提下进行子载波和中继分配。最后再进行功率分配获得性能进一步的提升。本节首先介绍PSO算法,然后采用MDPSO算法来进行子载波和中继分配,最后用迭代注水方法进行功率分配。
3.1 粒子群优化(PSO)
粒子群优化算法是一种基于群体智能随机搜索的全局优化算法。搜索过程从问题解的一个初始集合开始,系统由一群粒子(particle)组成。在搜索过程中采取最优解信息共享机制,即粒子飞行的策略只是追随自己当前的最好位置和整个群体当前的最好位置,整个群体就实现了对解空间中最好解的搜索。所以粒子群优化算法与其他的群体智能算法不同,在粒子群优化算法中,每个粒子是有记忆的,各自分别保留自己在搜索过程中找到的最好的问题解信息,而群体则保留当前的群体最好解信息。
粒子群算法中的每一个粒子包含着如下信息:
1) 粒子位置Xi,表示需要优化的变量;
2) 粒子速度Vi,表示在下一次迭代中粒子位置的变化;
3) 个体最优值pbesti,表示单个粒子所经历的最优值;
4) 群体最优值gbesti,表示所有粒子所经历的最优值。
在每次迭代中,每个粒子在空间中各自搜索,它的移动策略将根据自己的经验以及群体最优值共同决定。其速度和位置更新公式为[19]

其中,n为粒子个数,i表示粒子编号ω为惯性质量表示粒子保持之前速度的程度,1r和2r为2个均匀分布在[0,1]区间内的随机变量,1c和2c为学习因子分别表示粒子靠近自身最优值和群体最优值的权重。从社会心理学的角度来看,式(12)中的第2项为认知项表示个体采用自身成功经验的部分,而第3项为社会项表示其借鉴其他人成功经验的部分。
假设优化问题为最大化问题,则每个粒子在每次迭代中根据下面公式来更新其个体最优值

其中,()f·为需要优化的函数,这里用来评估粒子的适应度。
而群体最优值为
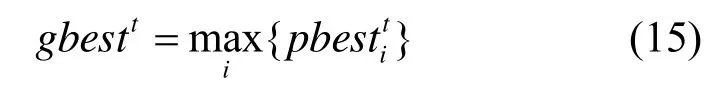
3.2 基于MDPSO的资源优化算法
传统的粒子群优化算法仅用来求解连续问题。而本文中的资源优化问题是个多维离散空间的优化问题。针对离散问题,粒子位置更新、速度更新等操作需要重新定义。本节将基于概率操作建立MDPSO算法,并用于求解资源优化问题。
首先,将子载波中继分配方案编码为离散空间的向量,也对应着粒子的位置。第i个粒子的位置可以表示为
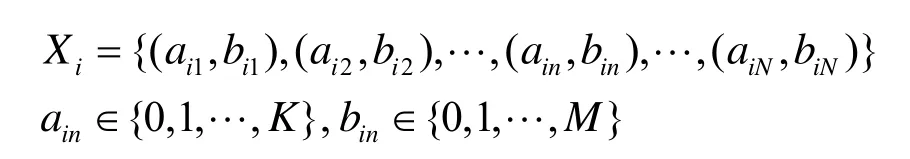
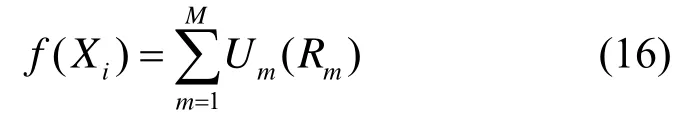
进一步定义离散空间向量的运算如下。
定义1 粒子位置的减法(得到速度)。
给定粒子的2个位置
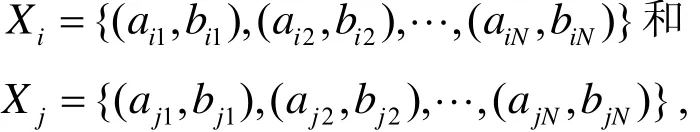
它们的距离定义为
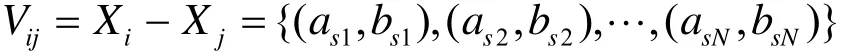
其中,
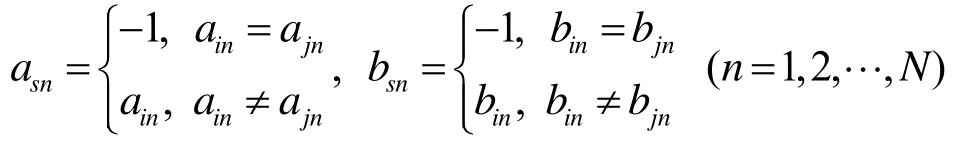
Vij中的(asn,bsn)表示将其第n项变为(asn,bsn),而-1表示没有变化。
定义2 粒子位置和速度的加法(得到新的位置)。
给定位置Xi={(ai1,bi1),(ai2,bi2),…,(aiN,biN)}和速度Vs={(as1,bs1),(as2,bs2),…,(asN,bsN)},定义它们的加法操作为
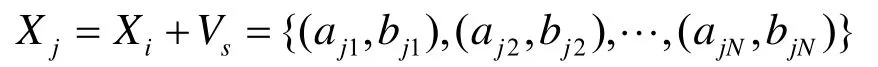
其中,
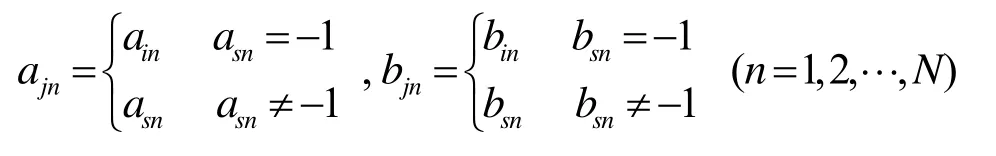
加法操作是减法操作的逆运算,然而此处是不需要满足交换律的。在MDPSO算法中,此操作用来更新粒子的位置。
定义3 多个速度的加权相加(得到新的速度)。
给定3个粒子速度变量:Vi={(ai1,bi1),(ai2,bi2),…,(aiN,biN)},Vj={(aj1,bj1),(aj2,bj2),…, (ajN,bjN)}和Vs={(as1,bs1),(as2,bs2),…,(asN,bsN)}以及3个比例因子c1,c2,c3≥0,它们的加权相加定义为V0=c1Vi+c2Vj+c3Vs={(a01,b01),(a02,b02),…,(a0N,b0N)}。
V0按照如下方式得到。
1)d1=round(N×c1/(c1+c2+c3)),d2=round(N ×c2/(c1+c2+c3))round (·) 表示取最近的整数。
2) 随机地从集合D= {1, 2, …, N}中选取d1个数,构成D1;然后从集合D-D1中选取d2个数构成集合D2,剩余的数构成D3=D-D1-D2。
3) 对V0中的每一个元素赋值,
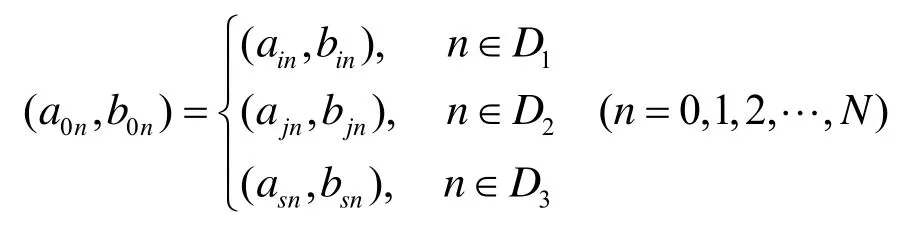
此操作用来完成MDPSO算法中的速度更新。它决定了粒子搜索的方向。其物理意义是在3个速度中求得加权合速度。由于离散空间内,同一直线上任何两不同点的距离相等,连续域的加权求和在离散空间中没有意义,这里采用了随机策略,使其反映了多维离散空间的特点。
定义4 粒子位置的变异操作(得到新的粒子位置)。
如果是适应度函数具有局部最优值,则粒子在迭代多次后很可能陷入局部最优。为了避免这种现象发生,引入了变异操作。
给定粒子的位置:Xi={(ai1,bi1),(ai2,bi2),…,(aiN,biN)}和变异因子λ∈[0,1]。
设变异后的位置为Mutate(Xi,λ)={(at1,bt1),(at2,bt2),…,(atN,btN)},其取值由以下操作得到。
1) 在Mutate(Xi,λ)中随机选取λN个元素(atn,btn)。
2) 对步骤1)中所选的λN个元素进行赋值
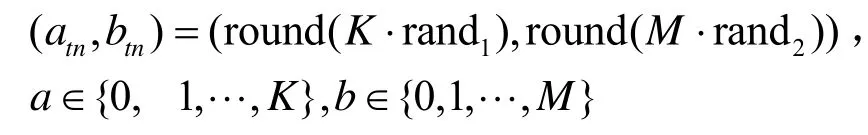
其中,rand表示在[0,1]中选取的均匀分布的伪随机标量。
3) Mutation(Xi,λ)中其余的元素和Xi中对应元素相同。
变异操作在位置更新中引入了随机因素,从社会心理学的角度上可以理解为个体的情绪。由此粒子的运动由以下3个因素影响:个体经验(pbest)、社会效应(gbest)、个体情绪(mutation)。
基于以上定义最终得到MDPSO算法如下所示。其中,最大迭代次数取值为50~100。变异因子λ取值为2/N。学习因子c1、c2和惯性质量ω均取为1。粒子群大小可以根据具体问题来确定,这里取值为50。
MDPSO算法

3.3 迭代注水法进行功率分配
上一节采用MDPSO算法完成了子载波中继分配问题,采用的是均匀功率分配方案。当功率资源足够丰富时此方法已经接近最优性能。当功率不充足时,可以采用功率分配技术来进一步提高性能。此时P1转化连续变量的优化问题。假定第一阶段基站到中继站之间的信道很好,这是符合实际场景的,因为可以基站和中继节点可以架设较高位置的天线,达到视距传输,同时在基站和中继站采用较高增益的天线来改进SNR。
首先,由式(6)得到拉格朗日函数为
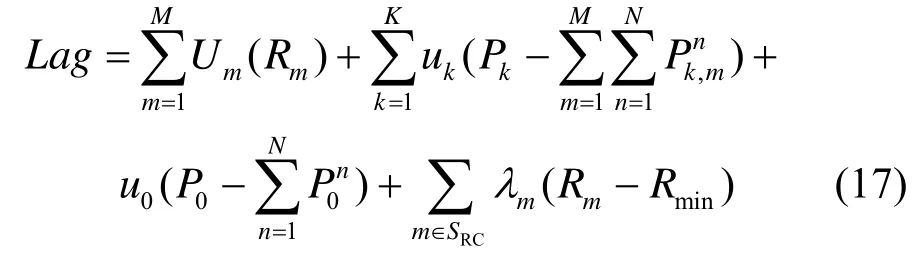
其中,uk为拉格朗日因子。对Lag求的微分得到:

应用Karush-Kuhn-Tucker (KKT)条件[20],由式(18)和式(19)得到最优功率分配为
迭代注水算法:迭代注水功率分配
1) 对每个RS 和BS将功率均匀分配在每个子载波上
2) 赋值迭代次数Max_iterations
3) t=1
4) While t≤Max_iterations do
6) 更新mR
7) End while
4 仿真结果和分析
仿真参数的设置参考了IEEE 802.16j OFDMA下行链路系统。考虑低速移动下的OFDMA小区网络,小区半径为1 km。中继站(RS)布置在距离基站(BS)2/3 km的位置。移动站(MS)的位置随机均匀分布在整个小区内。详细参数如表1所示。设定有14个BE用户,其效用函数分别为
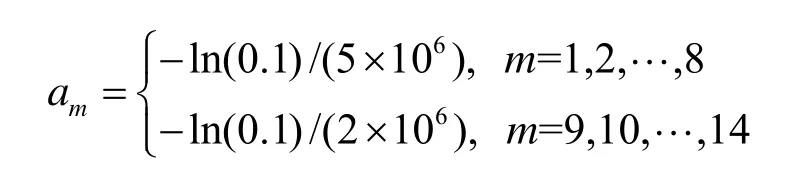
2个RC用户其速率约束为Rmin=1× 106bit/s 。为了对比,考察了5种不同算法组合的性能曲线,分别是:1)DPSO和注水功率分配联合算法(迭代次数t为80);2)文献[4]中的最大加权和速率迭代注水算法;3)随机子载波分配和注水功率分配;4)DPSO和均匀功率分配;5)DPSO 和注水功率分配联合算法(迭代次数t为20 000)。

表1 仿真参数
图3显示了不同RS数目时,DPSO算法的迭代收敛性。可以看到,总效用随着迭代次数增加而增加,但达到较高迭代次数时,逐渐饱和。说明粒子在最初迭代时迅速移动寻找最优值,而在多次迭代之后逐渐收敛到接近最优值。图中还显示随着RS数目的增加,效用也增加;但RS数目达到5时,性能也已经饱和,此时再继续增加RS数目对性能提升不大。此现象说明,当小区中RS数目达到一定程度后小区容量也将达到饱和。
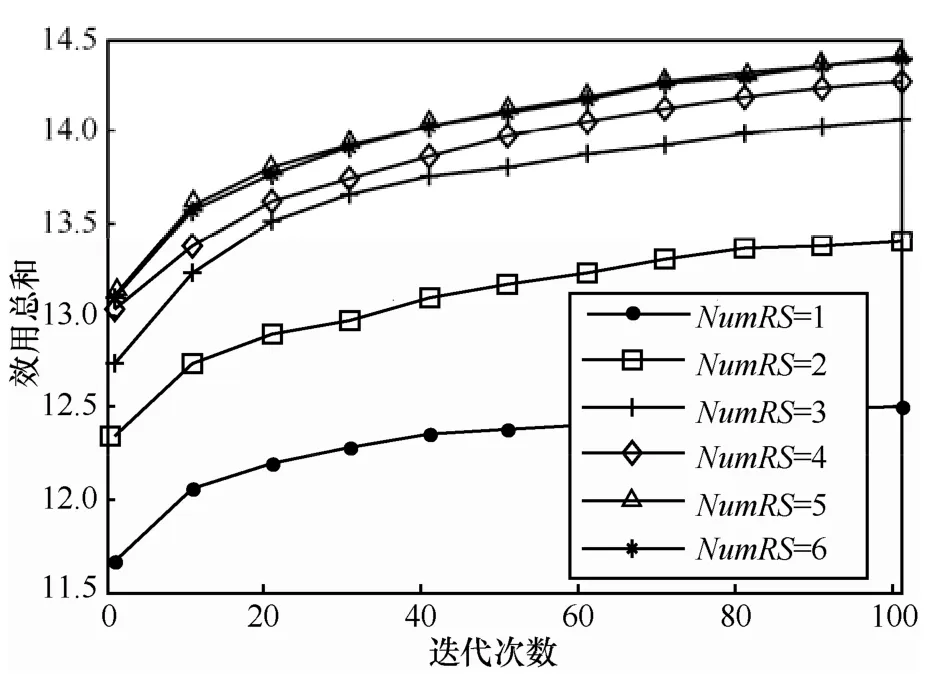
图3 DPSO算法的迭代收敛性
图4对比了在不同RS数目下,几种算法的效用函数。为了比较,同时仿真了迭代次数为80和20 000次的DPSO算法性能。可以看出,所提DPSO算法性能最优,在迭代次数为80次时已经取得明显优于文献[4]中算法的性能。从图中还可观察到即使是采用等功率分配的DPSO算法,其性能也可以达到较好值。这是因为子载波分配和中继分配保证了每个信道尽可能获得较高的SNR,而低SNR的信道被丢弃。在高SNR的情况下,等功率分配是近似最优分配方案。所以可以得知,在资源分配中,子载波分配和中继选择占据了更为重要的地位。
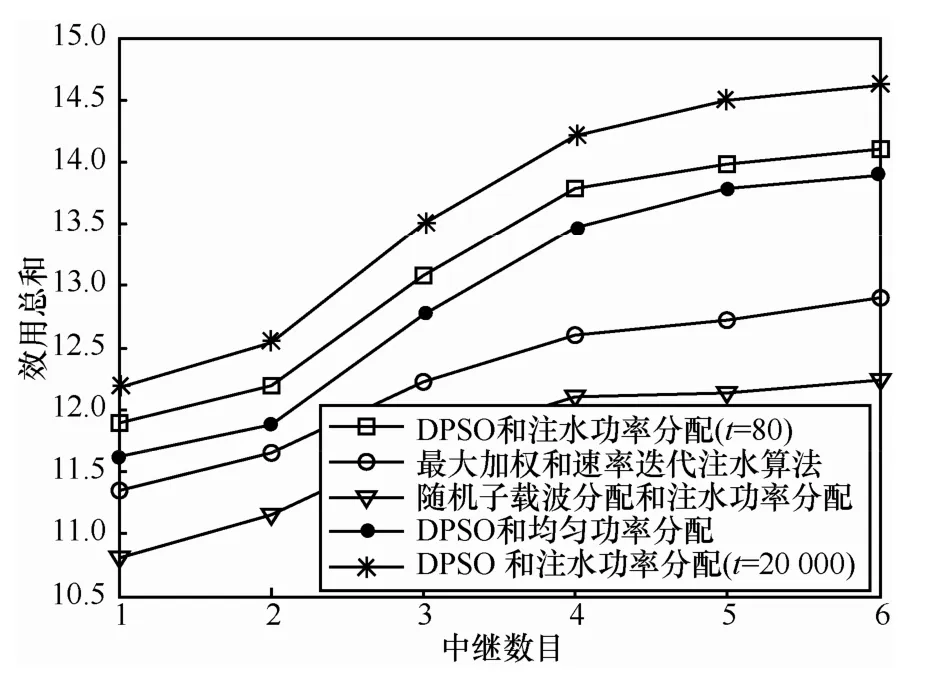
图4 不同RS数目下各种算法效用函数对比
图5对比了在不同RS数目下几种算法的吞吐量。可以看到所提DPSO算法的性能最优,在迭代次数为20 000次时,相比文献[4]中的算法性能提升了接近一倍;在迭代次数为80次时,有约50%的性能提升。只利用DPSO进行子载波和中继分配,而采用等功率分配时,性能相比文献[4]中的算法也有约20%的提升。由此看来,所提DPSO智能算法在离散和连续变量优化问题上性能比传统算法有明显优势。

图5 不同RS数目下各种算法吞吐量对比

图6 各种算法公平性指数对比

表2 各算法耗费时间对比(CPU AMD Athlon 64×2双核处理器3 800+ 2.0 GHz, 2 GB RAM)
表2进一步对各种算法的复杂度进行了比较,显示了各种算法在计算机上的运行时间。其中,RS数目为6。可以看到,所提算法运算时间约为文献[4]算法的3倍。注意到此结果由CPU上通过串行方式运行得到。实际中可以采用并行方式在FPGA(field programmable gate array)硬件上实现,而所提粒子群算法中各个粒子独自分别寻优,具有天然并行特性。理论上通过并行设计可将运行时间减少到约1/N(N=50为粒子群中粒子数量)。 所以本算法将来在工程应用中运算时间上也具备一定优势。
5 结束语
本文研究了协同OFDMA系统的跨层资源分配问题。考虑了多用户多服务的场景,即不同用户具有不同的效用函数。将此问题建模为离散连续变量的联合优化问题。根据多维离散空间的特点构建了新的MDPSO算法。此算法适合求解高维度离散空间优化问题,可以被广泛应用于解决各类大规模组合优化问题。利用所提MDPSO算法来进行子载波分配和中继选择,并用迭代注水法进行功率分配。仿真结果显示所提算法在效用函数和公平性2个指标上均明显优于已有算法。
[1] WANG T, VANDENDORPE L. WSR maximized resource allocation in multiple DF relays aided OFDMA downlink transmission[J]. IEEE Trans Signal Process, 2011, 59(8):3964-3976.
[2] LI H X. Dynamic resource allocation in OFDMA-Based DF cooperative relay networks[J]. Wireless Personal Communications, 2012,62(3):655-670.
[3] TASSIULAS L, SARKAR S. Maxmin fair scheduling in wireless networks[A]. IEEE infocom'02[C]. New York, 2002.763-772.
[4] PAN Y W, NIX A, BEACH M. Distributed resource allocation for OFDMA-based relay networks[J]. IEEE Trans Veh Technol, 2011,60(3): 919-931.
[5] KATOOZIAN M, NAVAIE K, YANIKOMEROGLU H. Utility-based adaptive radio resource allocation in OFDM wireless networks with traffic prioritization[J]. IEEE Trans Wireless Commun, 2009, 8:66-71.
[6] LIU C, ZHANG S, QIN X. Utility-based resource allocation in OFDMA relay networks with service differentiation[A]. IEEE WCNC[C].Cancun, Quintana Roo, 2011.72-77.
[7] FATHI M, TAHERI H. Utility-based resource allocation in orthogonal frequency division multiple access networks[J]. Iet Communications,2010, 4(12): 1463-1470.
[8] EBERHART R C, KENNEDY J. A new optimizer using particle swarm theory[A]. Proceedings of the Sixth International Symposium on Micromachine Human Science[C]. Nagoya, Japan, 1995.39-43.
[9] KENNEDY J, EBERHART R C. Particle swarm optimization[A].Proceedings of IEEE International Conference on Neural Networks[C].Piscataway, NL, 1995.39-43.
[10] MAHDAD B, BOUKTIR T, SRAIRI K. Strategy based PSO for dynamic control of UPFC to enhance power system security[J]. Journal of Electrical Engineering & Technology, 2009, 4(3):315-322.
[11] RAGLEND I J, RAGHUVEER C, AVINASH G R, etal. Solution to profit based unit commitment problem using particle swarm optimization[J]. Applied Soft Computing, 2010, 10(4): 1247-1256.
[12] FU X, LI A Q, WANG L P, etal. Short-term scheduling of cascade reservoirs using an immune algorithm-based particle swarm optimization[J]. Computers & Mathematics with Applications, 2011, 62(6):2463-2471.
[13] SHARMA N, TARCAR A K, ANTONY V, etal. On the use of particle swarm optimization for adaptive resource allocation in orthogonal frequency division multiple access systems with proportional rate constraints[J]. Information Sciences, 2012, 182(1):115-124.
[14] YUSOFF M, ARIFFIN J, MOHAMED A. An improved discrete particle swarm optimization in evacuation planning[A]. IEEE International Conference of Soft Computing and Pattern Recognition[C]. Malacca,2009. 49-53.
[15] PAREEK U, LEE D C. Resource allocation in bidirectional cooperative cognitive radio networks using swarm intelligence[A]. IEEE Symp. Swarm Intelligence[C]. Paris, 2011.1-7.
[16] LANEMAN J, TSE D, WORNELL G. Cooperative diversity in wireless networks: efficient protocols and outage behavior[J]. IEEE Trans Inf Theory, 2004, 50(12):3062-3080.
[17] SONG G, LI Y G. Cross-layer optimization for OFDM wireless networks-part I: theoretical framework[J]. IEEE Trans Wireless Commu,2005, 4:614-624.
[18] WEN-HSING K L, WAN J L. Utility-based resource allocation in wireless networks[J]. IEEE Trans Wireless Commun, 2007, 6:3600-3606.
[19] HU X, SHI Y, EBERHART R. Recent advances in particle swarm[A].IEEE International Congress on Evolutionary Computation[C]. 2004.90-97.
[20] BOYD S, VANDENBERGHE L. Convex Optimization[M]. Cambridge: Cambridge Univ Press, 2004.
[21] YU W, RHEE W, BOYD S, etal. Iterative waterfilling for Gaussian vector multiple access channels[J]. IEEE Trans Inf Theory, 2004,50(1):145-151.

