倩影重来 形数结合——解2014年浙江省数学高考理科第17题有感

●

(曹宅高级中学 浙江金华 321031)

翻开2014年浙江省数学高考理科试卷，迎面扑来的便是带着淡淡清香的理科第17题，这是一道久违之后又倩影重来的探索型应用题，是全卷中一道亮丽的“风景”.于是,笔者在答题之后仍觉醇香四溢，下面就该题的常规解法、学生的易错点、变换题解和教学建议方面谈谈个人的体会.

1 原题呈现

图1

例1如图1，某人在垂直于水平地面ABC的墙面前和点A处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小.若AB=15 m，AC=25 m，∠BCM=30°，则tanθ的最大值是______(仰角θ为直线AP与平面ABC的所成角).

2 解法探寻

故

3 解后反思

3.1 命制意图及考查功能

例1的情境熟悉，背景公平，很好地体现了高考考试说明及教学指导意见的有关精神；有效地检测了考生的数学建模和解模能力；较好地考查了考生的变量意识，即用代数的方法研究动态几何问题；重点考查了空间中点、线、面间平行、垂直的位置关系，考查了空间直二面角内线面角的探求.

3.2 常见错误及成因分析

例1解题的关键可以归结为建模和解模，据笔者对本题考情的调查，考生在解答过程中，可能出现的错误有：

(1)缺乏实际问题数学化、几何问题代数化的建模化归意识和基本功.

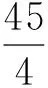
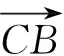
(2)缺乏解模答题方面的基本功.

在具体解答模型tanθ=f(x)的最值时，因缺乏对函数式f(x)作变形转化的“基本功”，从而导致解题中断.

3.3 题根溯源及变换再探

图2

4 教学启示

通过上面对例1的微探，我们不难体会到:尽管是一道高考试题，但所考查的还是《考试说明》及《教学指导意见》的基本要求——基本知识点、数学核心概念(如函数、变量等)、核心数学思想(如建模化归、形数结合等)、数学应用意识.因此，在平时的教学活动中，要注重以下3个问题：

(1)继续夯实基础，继续加强对数学核心概念及核心数学思想方法的教学与渗透.

加强核心概念的教学能使学生更好地抓住知识发生、发展的脉络与源泉，抓住本质；能更有利于学生建构起较为整体化、条理化、清晰化的良好学科知识体系；能更好地提高学生的学习兴趣，从而提高学生的学习成绩，提升教学质量.

(2)解题教学中继续注重通性通法，淡化特殊技巧，充分发挥典型例、习题的题根功能.

试题的命制要关注对数学概念本质的理解、数学理性思维、数学思想方法和解决数学问题的常规方法的考查(如例1中的变量法、换元法、配方法及数形结合思想等).虽说高考是一种选拔性考试，其试题具有一定的难易梯度，但大多数试题考查的还是“双基”，有些试题直接来源于教材中的某些例、习题，或由它们经过“加工演变”而成.因此,在平时的解题教学过程中，教师如果能够从一些典型的例、习题或最本源的数学基本概念、基本图形、基本原理出发，采用“变式”教学，让学生在教师有序并系统的变化中抓住题目“演变”过程中那些“不变”的东西，往往就能收到“解一题，通一类”之效果，解救学生于题海中.

(3)继续注重数学应用意识的培养，加强建模、化归、解模等基本功的日常教学.

依据现实的生活情境，提炼相关的数量关系建立起相应的数学模型，将现实问题化归为数学问题再加以解决，是解应用题中的重要环节，需要教师平时加以注重，有意识地渗透于日常教学中.