一图在手 万题莫挡——一个不可忽视的“立体几何”基本模型

●

(杭州学军中学 浙江杭州 310012)

“怎样让学生学好立体几何”这个问题一直困扰着我们，相当多的学生对“立体几何”课程望而生畏，尤其是女生，更是谈“立”色变.问题在何处?笔者认为，主要是由“立体几何”本身的特性所致.首先，它要求学生具有高度的空间想象力和严密的逻辑推理能力；其次，从“平面立体几何”到“立体几何”思维跨度太大，出现思维断层，加之“平面纸”上研究空间几何关系，就显得无从入手，很不适应.不少学生在学习“立体几何”时“丑态”百出，定理乱用；再则，由于空间向量工具的引入，更使学生感到找到了最后一根救命稻草，断然抛弃几何关系，做题就建系，导致对于空间问题中点、线、面等基本关系的判断全无感觉，更谈不上对空间关系的逻辑论证，立体几何的学习已完全失去其原本的教学意义.

学生无法用空间点、线、面等基本关系研究几何问题的关键在于：找不到几何关系的基本规律，觉得空间线面关系千变万化，错综复杂，找不到头绪，从而无所适从.为破解这个难题，笔者历时数年，专门对复杂纷繁的“立体几何”大题，尤其是历届高考“立体几何”大题进行分析、提炼，发现几乎所有考题均与一个基本模型相关，而这个基本模型中恰恰隐含了“立体几何”中所有的几何关系：即线线角(异面直线所成角)、线面角(直线与平面的所成角)、面面角(2个平面的所成角).这个基本模型是一个四面体，每个面均为直角三角形.鉴于它的重要意义，笔者把这个基本模型叫做“四直角四面体”.

“四直角四面体”是由“立体几何”中最基本、最核心的知识点提炼而成的模型，它的优越之处是抓住了“立体几何”的本质规律，提炼出的几个简单的基本关系揭示了“立体几何”的基本结构，可以快速求出各种空间角(线线角、线面角、面面角)，解题时只要准确识别题型模式，快速从复杂的“立体几何”图形中分离出基本模型，即可轻松解决千变万化的“立体几何”大题，让解题由难变易，化繁为简.

让学生牢固掌握“模型思维”，将会大幅提升学生的学习兴趣和学习效果，从而达到轻松提分的效果.同时，对立体几何这门学科也会有一个新的认识.

1 四直角四面体基本模型

定义每个面都是直角三角形的空间四面体称为四直角四面体(如图1).

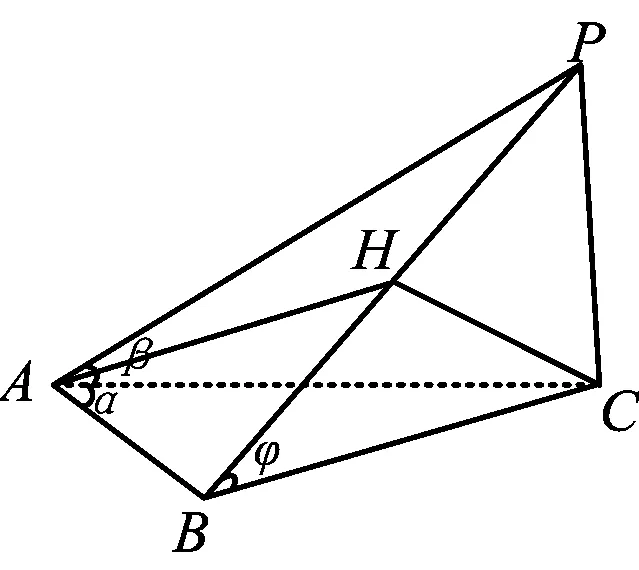
图1

若设β为斜线PA与底面ABC所成的线面角，δ为直线AC与侧面PAB的线面角，α为AB与斜线AP在底面ABC上射影AC的夹角，θ为AB与斜线AP的夹角，φ为斜面PAB与底面ABC所成二面角的平面角，ψ为斜面PAB与侧面APC所成二面角的平面角，则必有下列重要关系式：

(1)cosθ=cosαcosβ；

(4)sinδ=sinαsinφ.

证明已知PC⊥面ABC，作CB⊥AB，联结PB，由三垂线定理知，PB⊥AB.设AP=1，∠PAC=β,∠CAB=α,∠PAB=θ,∠PBC=φ,则在Rt△PAC中，

AC=cosβ,PC=sinβ；

在Rt△PAB中，

AB=cosθ,PB=sinθ；

在Rt△ABC中，

即

cosθ=cosαcosβ；

在Rt△PBC中，

由条件的对称性，可得

由面PAB⊥面PCB于PB，作CH⊥PB于点H，联结AH，则∠HAC=δ即为直线AC与侧面PAB的线面角.由于面HCB⊥面CBA于CB，于是

cos∠HCA=cos∠BCA·cos∠HCB,

即

亦即

sinδ=sinαsinφ.

为了使用方便，我们还可简化模型的制约条件，即只要三面角A-BDC中有2个面互相垂直即可.如图2，设∠BAD=β,∠CAD=α,∠BAC=θ,二面角B-AC-D的平面角为φ，二面角C-AB-D的平面角为ψ.若面ADB⊥面ADC(简记为β⊥α)，则

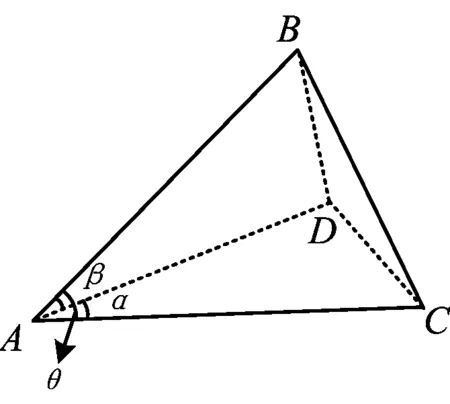
图2

(1)cosθ=cosαcosβ；

(4)sinδ=sinαsinφ.

简化后的模型，由于只需α⊥β(角α所在平面与角β所在平面)即可使用模型，为解题操作带来更大的方便，我们称这个简化的模型为“直三面角”模型.

这个模型具有强大的威力，几乎可以破解所有求角(线线角、线面角、面面角)的高考试题，故我们称其是最牛的基本模型.下举例说明之.

2 用基本模型求解线线角问题

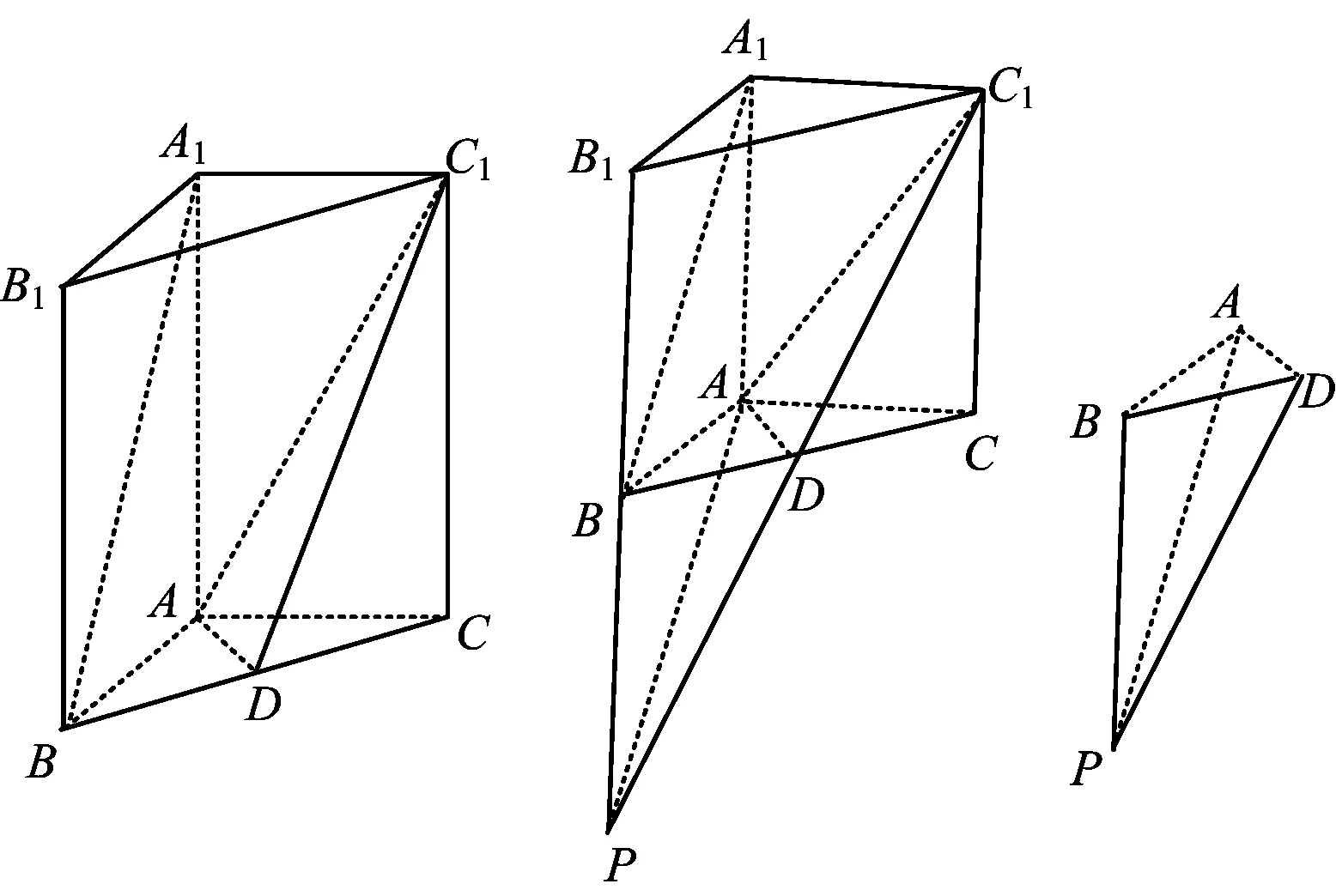
图3 图4 图5

例1如图3,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点,

(1)求异面直线A1B与C1D所成角的余弦值;

(2)求平面ADC1与ABA1所成二面角的正弦值.

(2013年江苏省数学高考试题)

解(1)略.

(2)如图4，延长C1D交B1B于点P，联结PA，则PA为平面ADC1与平面ABA1的交线.因为D为BC的中点，所以PB=BB1，则PBA1A为平行四边形，从而PA∥BA1，即∠APD为异面直线A1B与C1D所成的角.故所求问题即转化为在三棱锥P-ABD中求∠APD和二面角B-PA-D的平面角.

由题设知：PB⊥面ABD，则面PBA⊥面ABD，从而三面角A-PBD为“直三面角”模型，分离后如图5.

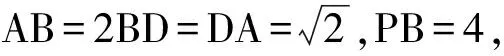
由“直三面角”模型公式，得

3 用基本模型求解线面角问题

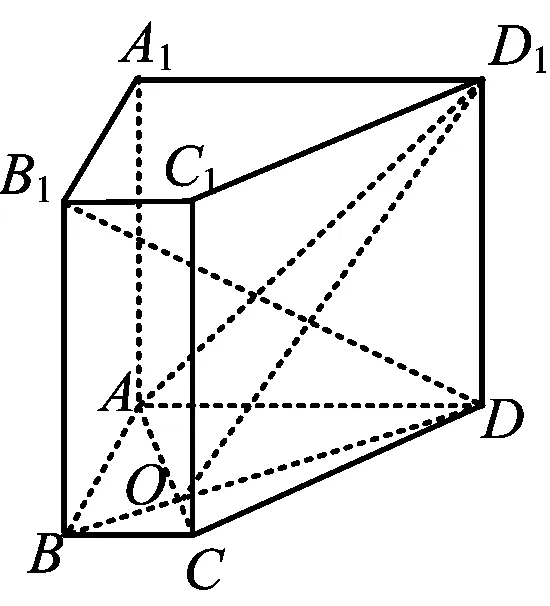
图6

例2如图6,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.

(1)证明:AC⊥B1D;

(2)求直线B1C1与平面ACD1所成角的正弦值.

(2013年湖南省数学高考理科试题)

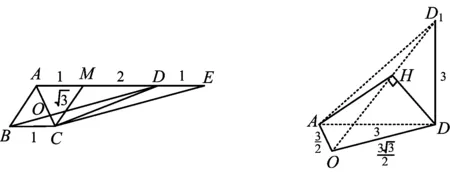
图7 图8

(1)略.

(2)解设AC∩BD=O，如图7，由∠BAD=90°，AC⊥BD,BC=1,得

因为ABCD-A1B1C1D1是直棱柱,所以三面角A-D1DO是“直三面角”模型，分离后如图8.

作DH⊥OD1于点H，联结AH，设∠D1AD=β=45°,∠DAO=α=60°,∠D1AO=θ,∠HAD=δ,则

例3(原创题)已知在四面体A-BCD中,∠DAB=30°,∠BAC=60°,∠CAD=45°,AB=4,AC=2,AD=3,求直线AC与面ABD所成角的余弦值.

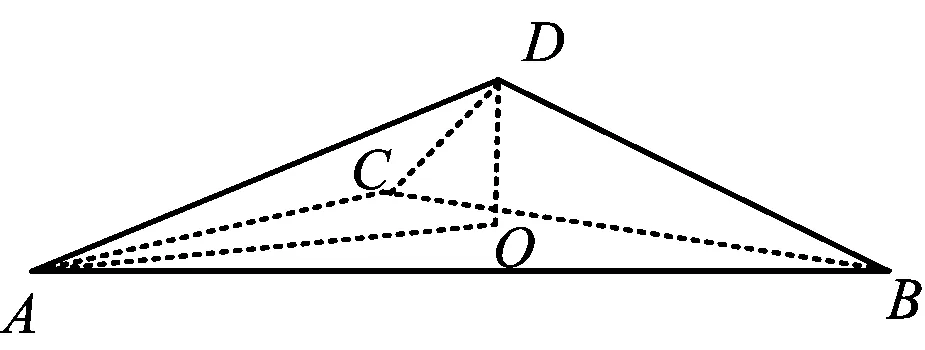
图9

解如图9,过点D作平面ABC的垂线交底面于点O，联结AO，则三面角A-DOC，A-DOB均为“直三面角”.

设∠DAO=β,∠CAO=α,∠DAC=θ=45°,∠BAO=α′,∠DAB=θ′=30°,α′=60°-α,则

cosθ=cosαcosβ,

即

同理可得

cosθ′=cosα′cosβ,

即

从而

故

4 用基本模型求解面面角问题

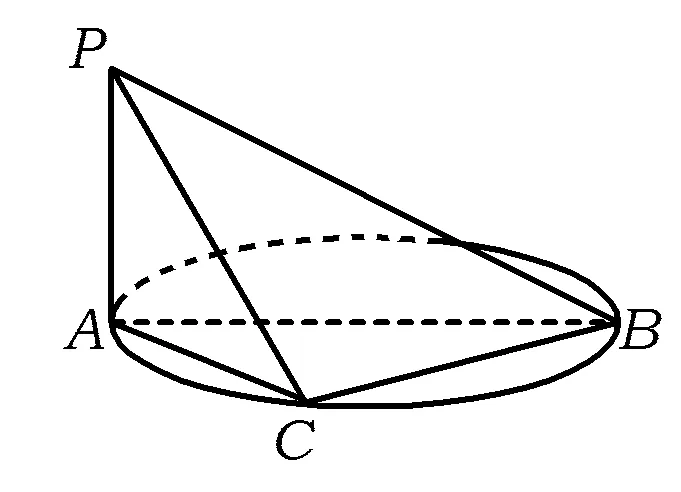
图10

例4如图10,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.

(1)求证:平面PAC⊥平面PBC；

(2)若AB=2，AC=1，PA=1，求二面角C-PB-A的余弦值.

(2013年辽宁省数学高考理科试题)

解(1)略.

(2)由题意知，面PAB⊥面CAB，故P-ABC为“直三面角”.设二面角C-PB-A的平面角为φ，则由“直三面角”基本关系得

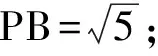
于是

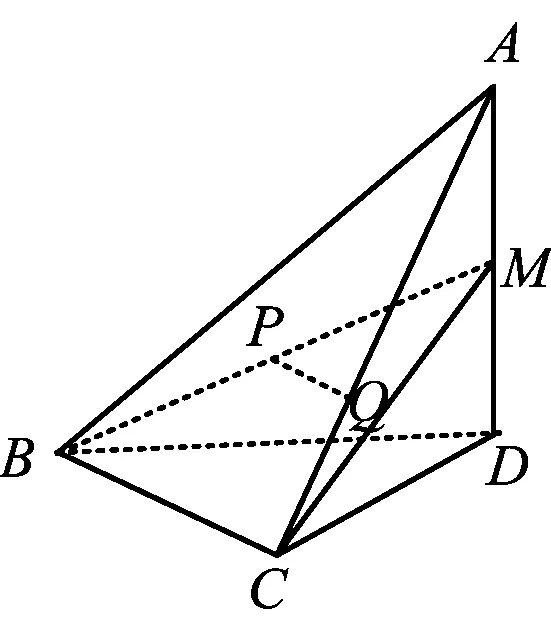
图11

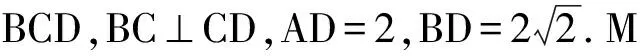
(1)证明:PQ∥平面BCD;

(2)若二面角C-BM-D的大小为60°,求∠BDC的大小.

(2013年浙江省数学高考理科试题)

解(1)略.

(2)由MD⊥面BCD,知B-MCD是“直三面角”模型.

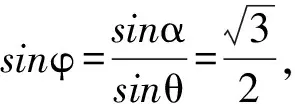
又因为

所以

即

4sin2α=1,

亦即

从而

α=30°,

故

∠BDC=60°.

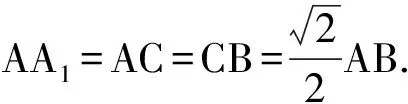
(1)证明：BC1∥平面A1CD；

(2)求D-A1C-E的正弦值.

(2013年全国数学高考课标卷理科试题)

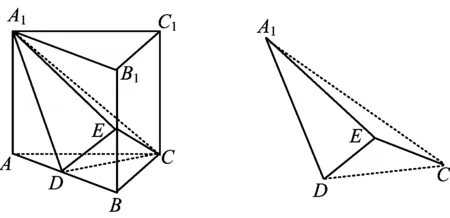
图13 图14

(1)略.

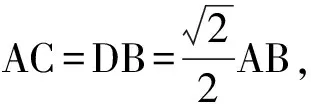
AC⊥BC.

又AD=DB,得

CD⊥AB,

从而三面角A1-EDC即为“直三面角”模型，分离如图14所示.

设∠EA1D=β，∠CA1D=α，∠CA1E=θ，二面角D-A1C-E的平面角为φ，则由“直三面角”基本关系得

从而

于是

5 用基本模型求解点面距离问题

例7(原创题)如图15,已知四面体A-BCD中,∠DAB=60°,∠BAC=45°,∠CAD=90°,AB=2,AC=2,AD=2,求顶点D到面ABC的距离.

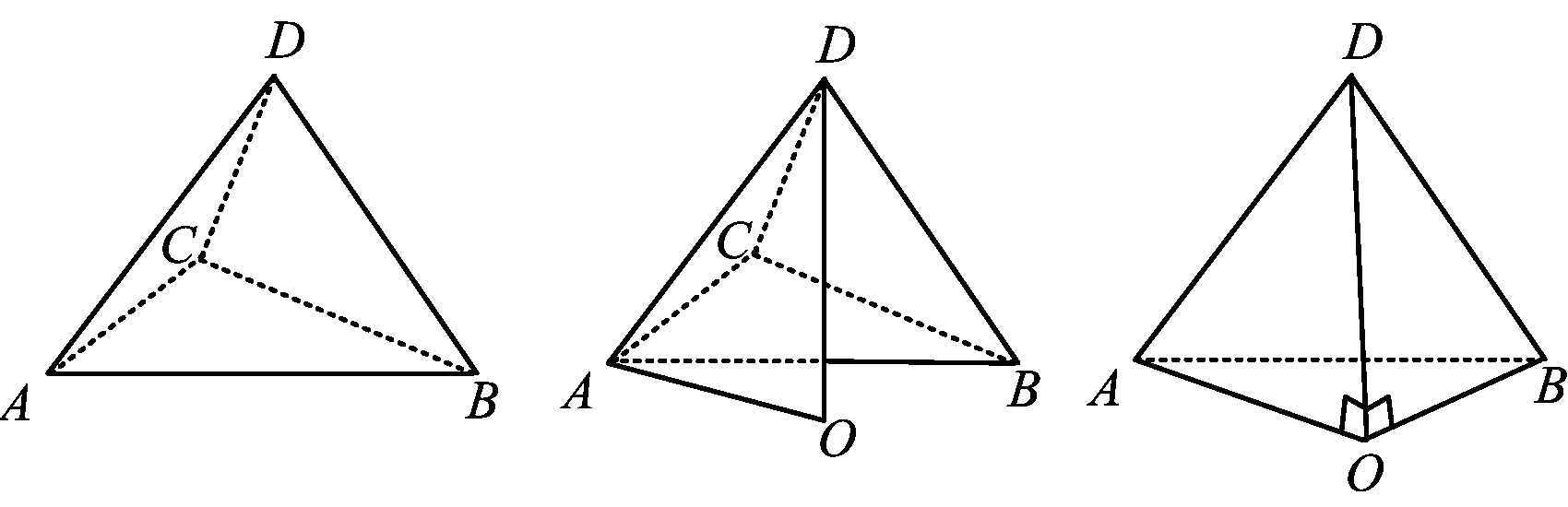
图15 图16 图17

解如图16,过点D作平面ABC的垂线交底面于点O，则DO即为点D到面ABC的距离.联结AO，则三面角A-DOB即为“直三面角”模型，分离如图17.

设∠DAO=β,∠BAO=α,∠DAB=θ=60°,则由“直三角面角”基本关系得

cosθ=cosαcosβ,

因为∠CAD=90°,DO⊥面ABC，所以∠CAO=90°.又∠BAC=45°,得

∠BAO=α=45°,

从而

cos60°=cos45°cosβ,

得

即

β=45°,

故

6 用基本模型求解体积问题

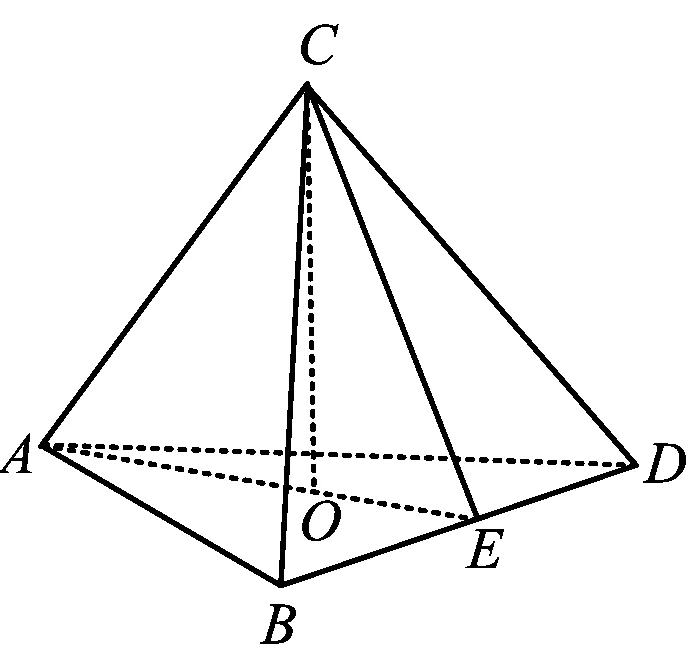
图18

例8(原创题)如图18,已知在三棱锥A-BCD中,∠BAC=45°，∠BAD=90°，∠CAD=60°，且AB=2，AC=3，AD=4,求三棱锥A-BCD的体积.

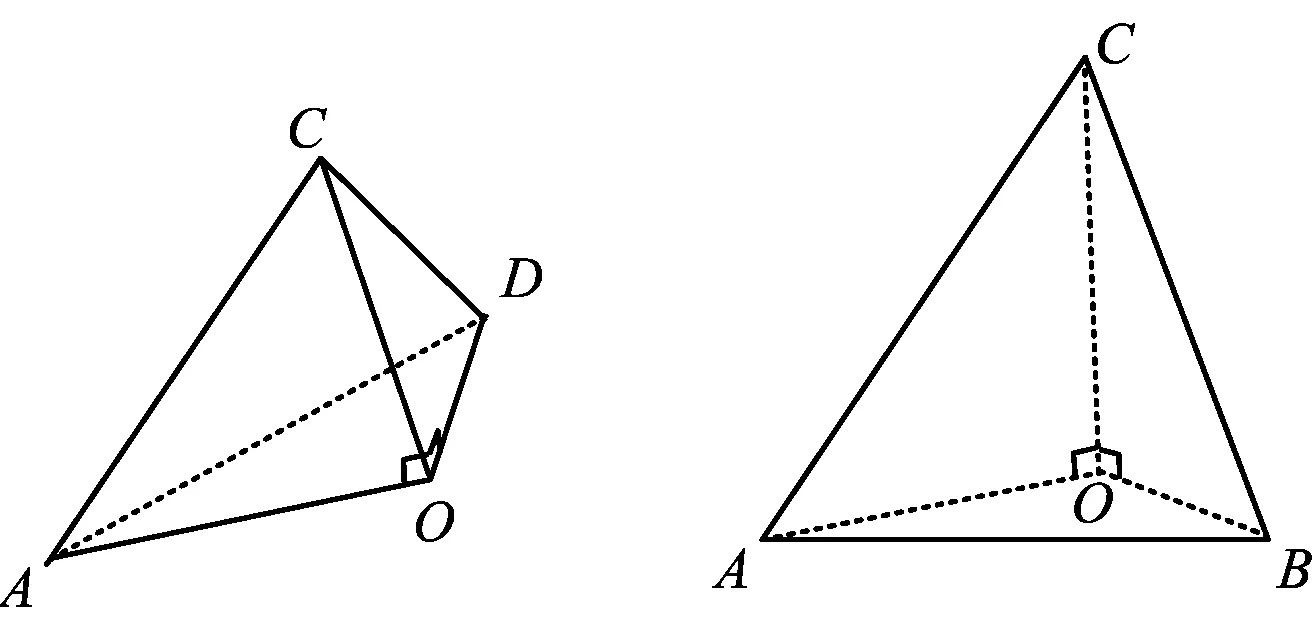
图19 图20

由“直三面角”基本关系得

cosθ=cosαcosβ,cosθ′=cosα′cosβ′,

即

cos45°=cosαcosβ,

从而

由

得

即

β=30°,

从而

于是

上述通过“基本模型”破解了各种类型的求角问题，由于篇幅所限，其余试题的破解只能忍痛割爱，读者可以自己尝试一一破解.