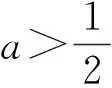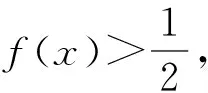解决含参恒成立问题的3种境界

●

(浙江师范大学附属中学 浙江金华 321004)

含参恒成立问题是函数中最常见、也是最复杂的一类问题，综合性强，变化多，对数学逻辑思维能力、等价转化能力和运算能力都有极高的要求.解决时往往找不到突破口，难以下手，或是找不对方向，常走弯路.

此类问题最基本的解决思路是最值转化，把问题转化为求某一函数在区间上的最大(或最小)值.导数法是解决该类问题有效的途径之一，但往往不是一次求导就能解决的，需要多次求导或利用导数的意义加以判断，更有甚者是抛开导数，直接利用“反客为主”法求解.

归结起来，解决此类问题有以下3种境界.

境界1

求导“一站到底”

利用函数的导数判断函数的单调性与最值，从而求出参数的取值范围.有时一次求导就能判断，有时需要多次求导，逐层判断单调性，称之为“一站到底”.

例1

关于x的不等式ex≥1+ax对x≥0恒成立，求实数a的取值范围．

分析

由题意，问题等价于不等式ex-ax-1≥0在[0,+∞)上恒成立.

设函数f(x)=ex-ax-1，x∈[0,+∞)，求导得

f′(x)=ex-a，

又x∈[0,+∞)，得ex≥1，从而

(1)当a≤1时，f′(x)=ex-a≥0，即f(x)=ex-ax-1在(0,+∞)上单调递增，因此当x∈[0,+∞)时，fmin(x)=f(0)=0．

(2)当a>1时，由f′(x)=0，得x=lna>0，从而f(x)=ex-ax-1在(0,lna)上单调递减，在(lna,+∞)上单调递增.又f(0)=0，于是当x∈(0,lna)时，f(x)

综上可得，实数a的取值范围是a≤1．

例2

关于x的不等式ex≥1+x+ax2对x≥0恒成立，求实数a的取值范围．

分析

由题意，问题等价于不等式ex-ax2-x-1≥0在[0,+∞)恒成立．

设函数f(x)=ex-ax2-x-1，x∈[0,+∞)，求导得

f′(x)=ex-2ax-1，

设g(x)=ex-2ax-1，x∈[0,+∞)，则g′(x)=ex-2a,又x∈[0,+∞),得ex≥1,从而

由上面2个例子可以看出，函数变化看导数，难分难解再追踪，函数零点或难求，导数意义仍可用！

境界2

借助高数方法

含参恒成立问题经常采用的另一种解决办法是分离变量，最值转化.但遇到比较复杂的问题，完全变量分离后求函数最值仍会遇到一些困惑，最常见的是最值点的函数值没有意义，若采用先猜想后证明的办法加以解决则比较复杂，若采用高等数学中的方法，则可以很快解决.最为典型的是利用洛必达法则求解.

洛必达法则：设函数f(x),g(x)满足：

(2)在a附近的去a区域内，f′(x),g′(x)都存在，且g′(x)≠0；

例3

关于x的不等式ex≥1+x+ax2对x≥0恒成立，求实数a的取值范围．

分析

当x=0时，不等式恒成立，故a∈R．

设g(x)=(x-2)ex+x+2，则g′(x)=(x-1)ex+1，再设h(x)=(x-1)ex+1，则h′(x)=xex.当x>0时，h′(x)=xex>0，可得h(x)=(x-1)ex+1在(0,+∞)上单调递增，即

h(x)>h(0)=0.

由此可知g(x)=(x-2)ex+x+2在(0,+∞)上单调递增，即g(x)>g(0)=0，因此当x>0时

境界3

反客为主，因式分解

有时含参问题不能彻底分离变量，用逐次求导方法又不能顺利解决，需要变换思维角度，变更主元，反客为主，将不等式视为关于参数的一元二次不等式．

例4

对任意x>0,关于x的不等式

[(a-1)x-1](x2-ax-1)≥0

恒成立，则实数a=______．

(2012年浙江省数学高考理科试题)

分析

一般思路是将不等式化为

(a-1)x3-(a2-a+1)x2+x+1≥0

对任意x>0恒成立，由三次函数的性质，可知a>1，故只要求

f(x)=(a-1)x3-(a2-a+1)x2+x+1

在x∈(0,+∞)上的最小值即可．

对f(x)求导，得

f′(x)=3(a-1)x2-2(a2-a+1)x+1,

令f′(x)=0，得

3(a-1)x2-2(a2-a+1)x+1=0.

至此，学生无法顺利求解下去，用导数方法很难求出f(x)在x∈(0,+∞)上的最小值.也就是说，利用导数法解决此类含参不等式恒成立问题会遇到障碍．

换一种角度思考，若将不等式变形为

[ax-(x+1)][ax-(x2-1)]≤0，

则由x>0，上式可化为不等式

[a-h(x)][a-g(x)]≤0

对x>0恒成立，故a-h(x)与a-g(x)异号或其中一个式子为0.又由h(x)=g(x)且x>0，可得x=2．

此类问题还可以进行各种变化：

(1)若b为常数，f(x)=kx+m(k≠0)，则

[a-(kx+m)](a-b)≤0

恒成立，即为一般含参一次不等式恒成立；

(2)若f(x),g(x)均为一次函数，则

[a-f(x)][a-g(x)]≤0，

即构造出二次含参不等式恒成立问题；

(3)若f(x)为一次函数，g(x)为二次函数，则[a-f(x)][a-g(x)]≤0，即构造出三次含参不等式恒成立问题．

继续这样的构造，变换函数形式，还可以构造出一系列含参恒成立问题(此处不再赘述)．