椭圆最大面积内接n边形的性质

●

(乐清中学 浙江乐清 325600)

众所周知，圆的内接n边形当且仅当其为正n边形时具有最大面积．以此为基础，运用面积投影的方法[1]，可以得到定理1．

定理1

图1

证明

沿用上面的符号与图形，还可得到定理2．

定理2

重型颅脑损伤在临床上具有较高的致残率和死亡率，其主要病理变化为颅内压持续性升高，且患者伴有不同程度的神经功能缺损，故临床上治疗的关键是有效降低患者颅内压、改善其神经功能[8]。常规颞顶骨瓣开颅术由于受到骨窗限制，只能行局部颅内减压，无法达到快速、彻底减压效果。近年来，标准大骨瓣减压术广泛应用于治疗颅脑损伤患者，可以起到彻底清除患者血肿、快速降低颅内压等效果[2]。

证明

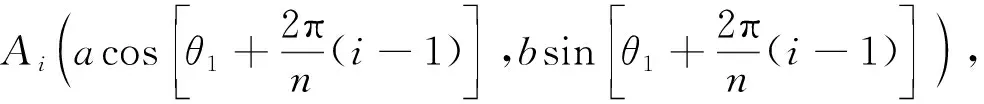
从而△OAiAi+1的面积

这说明每个△OAiAi+1的面积相等，虽然它们不全等．

依据面积最大内接多边形的几何特性，容易推想定理3．

定理3

当i=2,3,…,n-1时，直线li′的斜率为

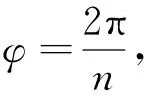
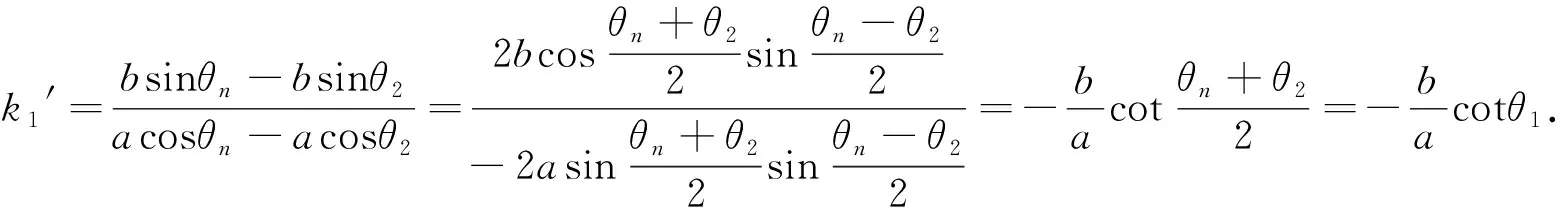
综上可知ki=ki′，且当ki不存在时，ki′也不存在，故li∥li′(i=1,2,…,n)．

运用三角与复数知识还可得到定理4．

定理4

证明

此性质说明，椭圆最大面积内接多边形的重心在椭圆的中心．

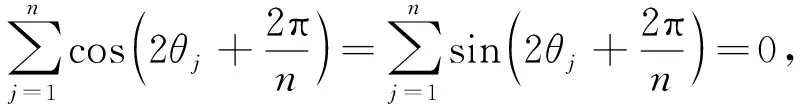
(4) |A1A2|2+|A2A3|2+…+|An-1An|2+|AnA1|2=

参 考 文 献

[1] 张普元．椭圆内接三角形最大面积的简易求法[J]．中学生数学，2002(12)：27．