基于时变可靠度理论的在役海洋平台结构构件剩余寿命预测*

周 雷李志刚陈祥余周道成

（1.海洋石油工程股份有限公司； 2.大连理工大学深海工程研究中心）

基于时变可靠度理论的在役海洋平台结构构件剩余寿命预测*

周 雷1李志刚1陈祥余1周道成2

（1.海洋石油工程股份有限公司； 2.大连理工大学深海工程研究中心）

以时变可靠度理论为基础，给出了在役海洋平台结构构件剩余寿命预测算法，结合算法给出基于目标可靠度指标的海洋平台结构构件剩余寿命的预测判据。以抗力衰减模型和荷载模型为基础，对渤海海域某平台典型管节点的剩余寿命进行了预测，并将预测结果与基于Miner线性疲劳损伤累积方法的估算结果进行了对比分析，结果表明了本文方法的有效性和可靠性。

时变可靠度理论；海洋平台；结构构件；抗力衰减；剩余寿命预测

海洋平台体积庞大、结构复杂、施工困难、造价昂贵，设计寿命一般在15～20年。与陆地结构相比，海洋平台既要受到潜在地震作用、台风等威胁，又要在恶劣的海洋环境条件下受到地基土冲刷和基础动力软化、环境腐蚀、海生物附着、材料老化、构件缺陷与损伤、疲劳和裂纹扩展的损伤积累等不利因素的影响，造成平台结构抗力衰减而影响结构的服役安全性和耐久性，导致海洋平台结构安全运行的风险加大。由于海洋环境的复杂性和随机性，历史上人们对这些作用的认识不足，不清楚各种环境因素的联合作用机理、结构损伤积累的过程及抗力衰减规律，以致于国内外发生过多起海洋平台事故，造成了不必要的人员伤亡、重大的经济损失和不良的社会影响。由于海洋平台结构构件的抗力随时间变化而发生衰减，其可靠性也随服役时间而发生变化，因此在预期的目标可靠度指标下推算结构的使用寿命，对结构构件剩余寿命进行预测，对于结构的维护和维修决策具有重要的意义。本文以时变可靠理论为基础，给出了平台构件极限承载力寿命预测算法，选择平台结构典型管节点进行剩余寿命预测分析，并将结果与Miner线性疲劳损伤累积方法进行了对比分析，结果表明本文方法更具有效性和可靠性。

1 基于时变可靠度的构件剩余寿命预测算法

基于结构时变可靠度理论，结合结构失效状态的可靠指标限值，可确定该可靠指标对应的使用年限，从而实现对结构构件剩余寿命的预测。结构使用寿命、已服役时间和剩余寿命之间的关系如图1所示，假定确定的构件目标可靠度指标为β0，可靠度安全限值为［β］，初始使用年限为t1＝T0，时变可靠度指标为β（t），基于时变可靠度理论的构件剩余寿命预测算法总体框架如图2所示。

目标可靠度指标是结构设计的依据，是结构设计所要预期达到的指标。周道成［1］采用校准法确定了我国海域平台的各类构件目标可靠度；JCSS规范中对于结构的失效后果等级和采取安全措施的相对成本的等级也具有明确的规定。海洋平台结构为重要的工业生产设施，一旦破坏，可能造成严重的经济损失和巨大的环境污染，失效后果严重；加之海洋环境复杂，导致采取安全维护措施的相对成本较高。因此，本文对平台管节点的目标可靠度指标取β0＝3.7，参考有关文献［2-4］取可靠度指标安全限值［β］＝0.85β0作为结构寿命终止的标志。

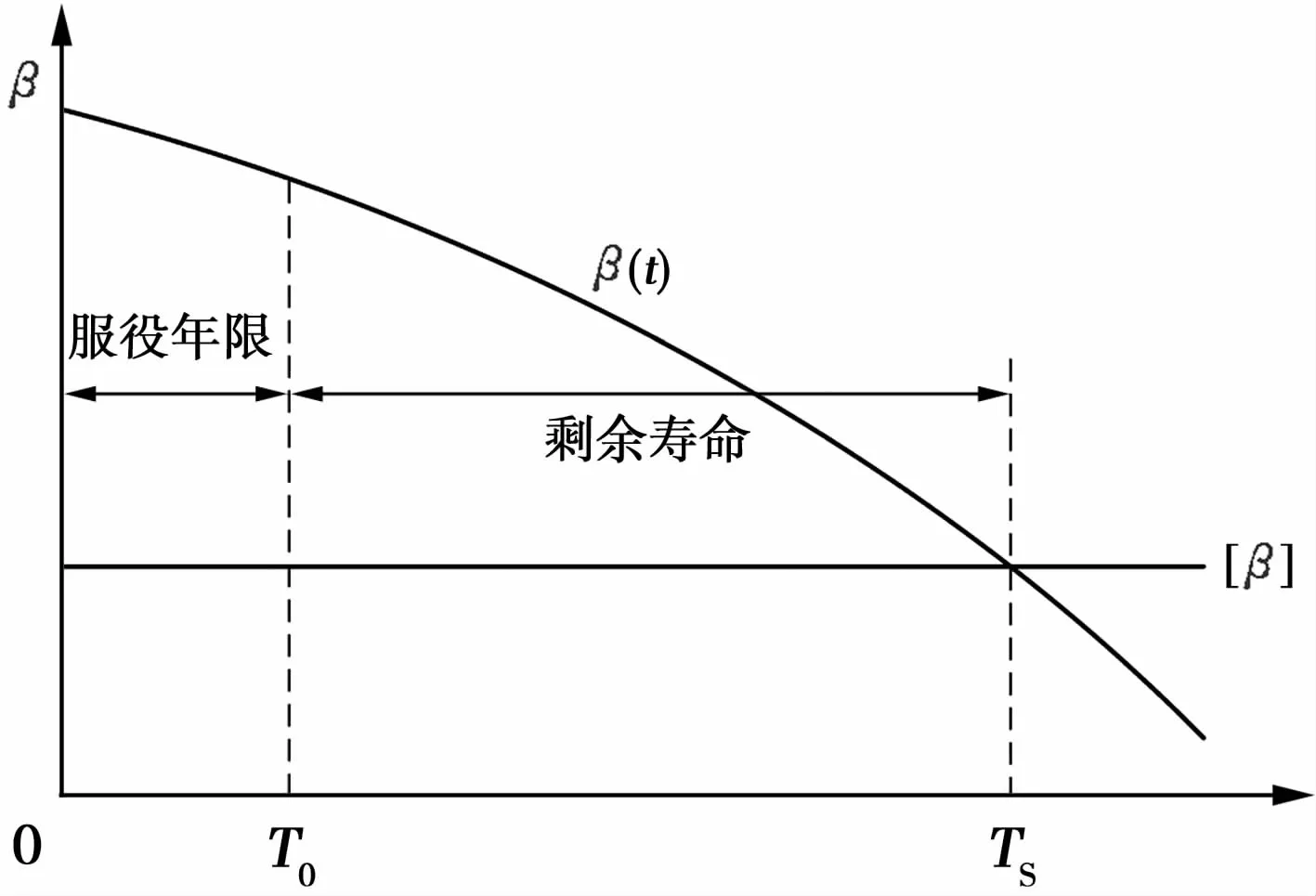
图1 寿命预测方法示意图

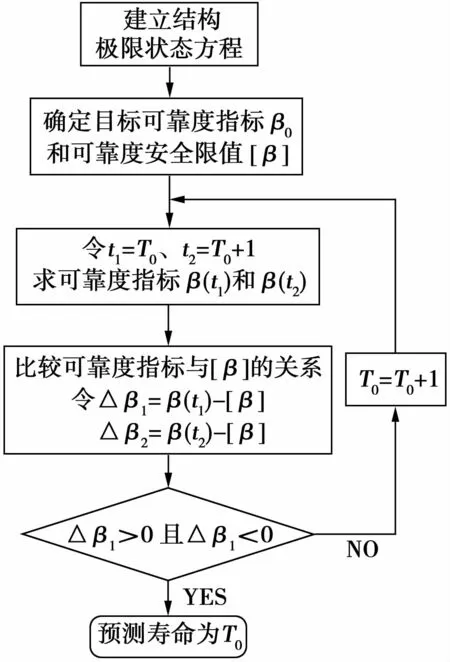
图2 基于时变可靠度理论的构件剩余寿命预测算法总体框架

2 构件抗力衰减计算

海洋平台结构构件的抗力是随时间变化而衰减的，因此其可靠性也随服役时间而变化。本文将利用文献［5］提出的方法，首先建立材料屈服应力随损伤发展而衰减的模型，为结构在使用期间的可靠度分析提供基础。建立材料屈服应力随损伤发展而衰减的模型，定义材料经历疲劳损伤D后，屈服应力

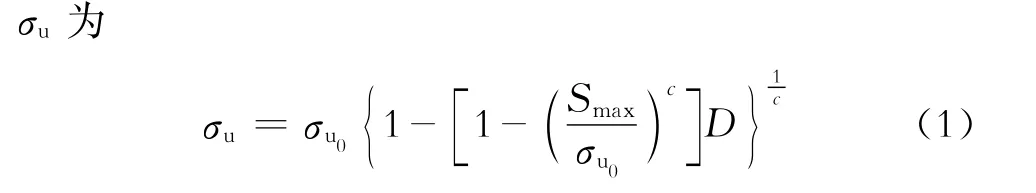
式（1）中：σu0为材料完好无损时的屈服应力；Smax为循环最大应力；D为随机荷载作用下的疲劳累积损伤率；c为常数，对于海洋平台结构一般取c＝1.25。

依据API RP 2A-LRFD标准给出的管节点在不同受力条件下对应的抗力计算表达式，求得抗力标准值，并根据对抗力各影响因素随机性的统计结果和材料屈服应力的衰减关系来确定管节点的抗力统计参数及衰减规律，海洋平台管节点参数示意图如图3所示。

图3 海洋平台管节点参数示意图

斜撑冲剪校核时轴向拉压抗力Pa和弯曲抗力Ma分别为

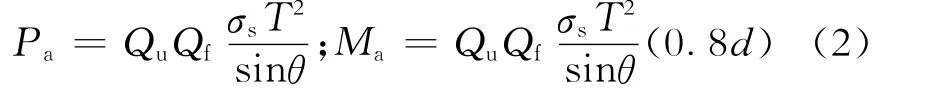
式（2）中：σs为结构材料的屈服强度；T为弦杆壁厚；d为斜撑直径；θ为斜撑轴线与弦杆轴线的夹角；Qu为极限强度系数；Qf为考虑弦杆中存在轴向名义应力的修正系数；Qu和Qf的取值可参见文献［6-7］。为计算管节点抗力的衰减规律，定义屈服应力衰减因子φ（t）为

根据管节点斜撑抗力计算公式（2），可知节点抗力与材料屈服强度为线性关系，则节点抗力在疲劳荷载作用下随时间的衰减关系可以表示为

式（4）中：屈服应力衰减因子φ（t）为确定性的时间函数，抗力初始值R0为随机变量，且分布特征参数已知，这样结构服役一定时间t后构件的抗力R（t）的分布特征及其参数可以获得。

3 设计荷载标准值及随机荷载的统计特征

平台结构可靠度计算需要设计荷载标准值及随机荷载的统计特征。海洋平台结构的荷载标准值可以参考其他结构（如建筑结构）的荷载（如地震和风）标准值确定，同时考虑到与API RP 2A-LRFD标准关于海洋结构荷载标准值的衔接性，荷载标准值取为100年一遇最大值。

各种荷载的统计特征是结构可靠度分析和设计的基础。荷载的统计特征由荷载的均值系数κXi、变异系数δXi和概率分布类型来表达，均值系数和变异系数分别定义为

式（5）中：μXi、σXi分别为荷载Xi的均值和标准差；Xik为荷载Xi的标准值。

海洋平台结构所受荷载主要分为非环境荷载与环境荷载。非环境荷载主要包括自重荷载和甲板动荷载。大量的统计假设检验表明，海洋环境中的风速、浪高、流速和冰厚年极值要素都很好的服从极值Ⅰ型分布。

4 数值算例

以渤海海域某油田导管架平台作为算例。该平台所处油田区域平均水深18.2 m，2003年投产，设计年限15年。图4为该导管架平台的立面及荷载作用示意图。根据该平台实测数据计算得到的管节点年累积疲劳损伤率，再由公式（1）计算求得管节点材料屈服应力随时间的衰减关系（时间以年为单位，初始屈服强度取为315 MPa），计算结果列于表3。基于公式（2）及API规范中对于参数计算方法的规定，求得抗力公式中各个参数取值，并求得节点斜撑轴向拉压抗力标准值，结果列于表4。

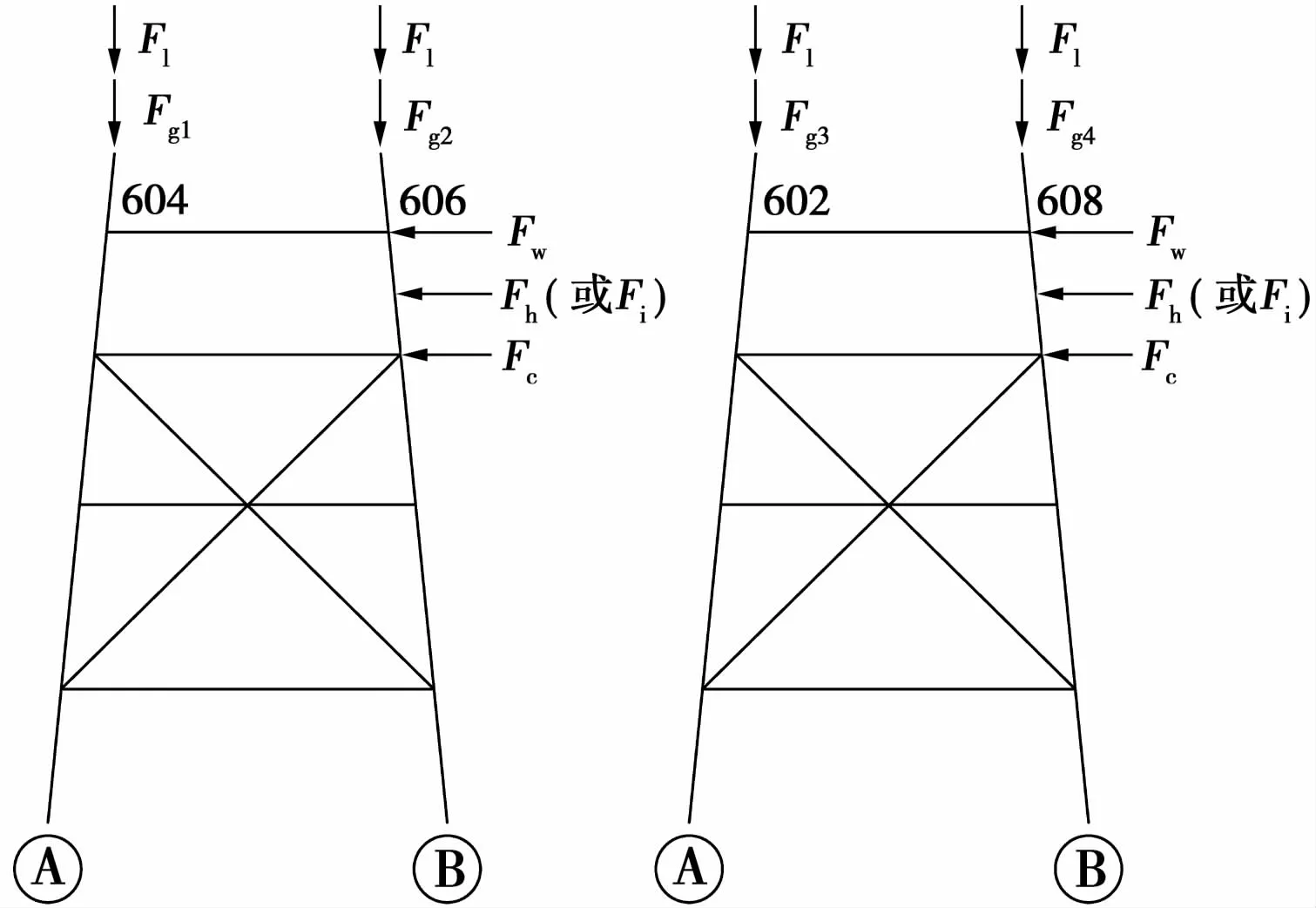
图4 渤海某油田导管架立面及荷载作用示意图

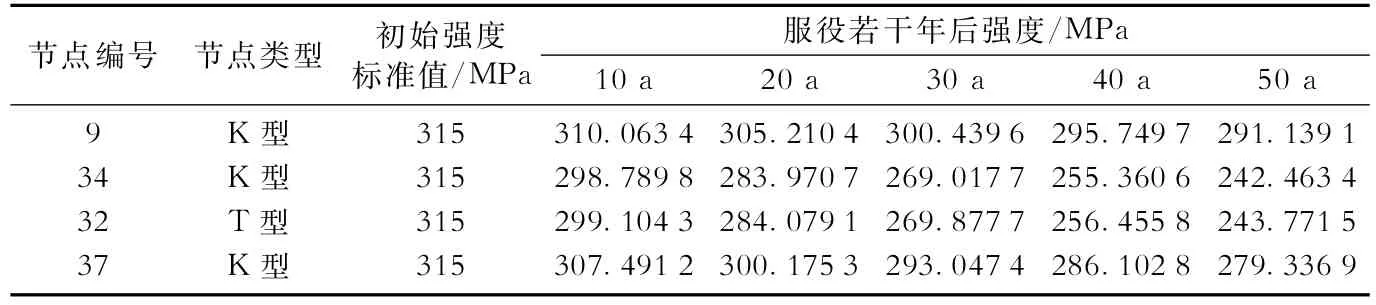
表3 渤海某油田导管架平台管节点材料屈服应力衰减计算结果

表4 渤海某油田导管架平台管节点斜撑冲剪轴向拉压抗力标准值

文献［8-10］对材料性能（强度、刚度等）的不确定性、构件几何参数的不确定性和抗力计算模式的不确定性进行了统计分析。根据API规范中不同抗力的计算方法和文献［8-10］构件抗力各随机因素的统计结果，并结合该平台的典型构件和管节点计算公式得到了其构件抗力的统计参数，结果列于表5。根据公式（3）计算得到了节点的屈服应力衰减因子，结果列于表6。

该平台的荷载作用方式如图4所示，荷载标准值取值见表7，其中Fg1、Fg2、Fg3和Fg4分别表示作用于4根导管腿工作点的上部自重荷载；Fl表示作用于4根导管腿工作点的甲板动荷载；Fw、Fh、Fc和Fi分别表示作用于导管钢架上的风荷载、波浪荷载、流荷载和冰荷载。

［11］，基于各种环境荷载的计算公式，并且将各极值环境荷载合理地假定为极值Ⅰ型分布，该平台环境荷载的年极值分布统计特征见表8。

结合前面抗力衰减模型和荷载概率模型，以及确定的结构失效对应的可靠指标安全限值，采用本文方法可计算获得该平台管节点的使用寿命和剩余寿命，结果列入表9。由表9的计算结果可知，该平台管节点的剩余寿命较长，管节点的安全储备较高。需要说明的是，本文所计算的管节点构件抗力衰减只考虑疲劳荷载，并未考虑海水腐蚀等其他作用的影响。

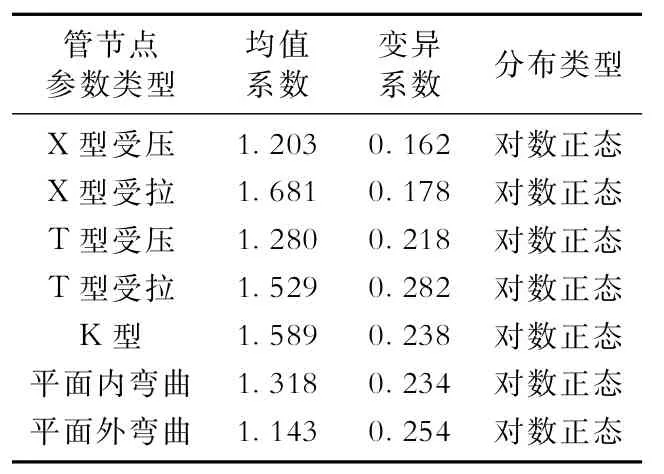
表5 渤海某油田导管架平台构件抗力的统计参数

表6 渤海某油田导管架平台节点屈服应力衰减因子

表7 渤海某油田导管架平台设计荷载标准值

表8 渤海某油田导管架平台荷载的统计特征参数

表9 渤海某油田导管架平台管节点构件寿命预测结果

基于Miner线性累积损伤理论［12］，由管节点年疲劳累积损伤指标亦可直接得到该平台管节点疲劳寿命的估算值，结果见表10。

对比本文方法与基于Miner准则的构件寿命估算结果，可知2种方法的预测结果较为接近，说明了本文方法的有效性。另外，基于Miner准则得到的构件寿命值更大一些，这是由于Miner准则是通过构件材料损伤累积计算估算寿命，当累积损伤率达到1时构件破坏。但是，在构件实际服役期间，由于极值荷载的存在，构件材料的抗力还未衰减到0时（即累积损伤率为1），因不满足极限承载能力要求而有可能发生破坏。而本文方法是将疲劳累积损伤考虑为极限承载力的影响因素，并考虑了荷载、结构重要性（结构失效安全可靠指标值）等因素。因此，基于本文方法计算所得的寿命值要相对更可靠一些。

表10 基于Miner准则得到的渤海某油田导管架平台管节点寿命估算结果

5 结论

本文以时变可靠度理论为基础，给出了基于时变可靠度理论的平台构件极限承载力寿命预测算法，将疲劳荷载作为抗力衰减的因素，选择渤海海域某油田导管架平台结构上具有代表性管节点进行了剩余寿命预测，并将预测结果与基于Miner准则的估算结果进行了对比分析，可得到以下2点主要结论：

1）海洋平台结构管节点极限承载力使用寿命主要取决于构件抗力衰减规律和目标可靠度指标，前者与管节点的疲劳累积损伤密切相关，后者与结构重要性、失效后果等有关。

2）管节点极限承载力使用寿命通常小于管节点疲劳寿命，这与定性分析结果一致。

参考文献

［1］ 周道成．导管架平台结构的可靠度设计与安全监测评定［D］．哈尔滨：哈尔滨工业大学，2006．

［2］ 四川省建设委员会．GB50290—1999民用建筑可靠性鉴定标准［S］．北京：中国建筑工业出版社，1999．

［3］ ALFERDO H S，ANG，WILSON H T．Probability concepts in engineering planning and design［M］．John Wiley＆Sons，1984．

［4］ 李运生，张彦玲．在役公路钢筋混凝土梁剩余寿命估算方法研究［J］．铁道标准设计，2003（1）：13-16．

［5］ 段忠东，欧进萍．基于概率疲劳累积损伤理论的构件抗力衰减分析［J］．哈尔滨建筑大学学报，1996，29（1）：1-8．

［6］ American Petroleum Institute．API RP 2A-LRFD［S］．Washington D C，2002．

［7］ 陆文发，李林普，高明道．近海导管架平台［M］．北京：海洋出版社，1992．

［8］ HSE（Health Safety Executive）．Component-based Calibration of north west European annex Environmental load factors for the ISO fixed steel offshore structures code 19902［R］．Research Report 088，2003．

［9］ FRED M，BERNHRD S．Calibration issues in development of offshore mechanics and arctic engineering［J］．Journal of Offshore Mechanics and Arctic．Engineering，2000，122（1）：52-56．

［10］ MICHEAL FABER．JCSS probabilistic model code part3：material properties［S］．Joint Committee on Structural Safety，2001．

［11］ 欧进萍，段忠东．基于随机裂纹扩展机制的构件抗力衰减分析［J］．机械强度，1994，16（3）：46-51．

［12］ MINER M A．Cumulative damage in fatigue［J］．Journal of Applied Mechanics，1945，12（3）：159-164．

The residual life prediction for in-service offshore platform structure members based on time-dependent reliability theory

zhou Lei1Li zhigang1Chen Xiangyu1zhou Daocheng2
（1.Offshore Oil Engineering Co.Ltd.，Tianjin，300451；2.Deep Ocean Engineering Research Center，Dalian University of Technology，Liaoning，116024）

Based on time-dependent reliability theory，this paper presents a residual life prediction method for in-service offshore platform structure members．The residual life prediction criteria and its algorithm for offshore structure members have been proposed based on the target reliability index．The resisting force model and structural load models being two important aspects of this method have been applied in the numerical cases．The residual life prediction for typical offshore platform structure member joints in Bohai Sea has been done and the results has been given to compared with the Miner criterion method，The analysis results show the availability and reliability of the proposed method．

time-dependent reliability theory；offshore platform；structure members；resisting force；residual life prediction

2012-12-25改回日期：2013-03-10

（编辑：叶秋敏）

*国家高技术研究发展计划（863计划）（项目编号：2008AA092701）部分研究成果。

周雷，男，1978年生，博士，高级工程师，主要从事海洋工程设计和研究工作。地址：天津市塘沽区丹江路1078号（邮编：300451）。E-mail：zhoulei＠mail．cooec．com．cn。