累积增长预测模型的典型曲线及应用

陈元千 邹存友 于立君

（中国石油勘探开发研究院）

累积增长预测模型的典型曲线及应用

陈元千 邹存友 于立君

（中国石油勘探开发研究院）

预测模型按产量和累积产量的变化特征可分为单峰周期模型和累积增长模型，前者包括翁氏模型、威布尔模型、瑞利模型、陈-郝模型和广义模型，后者包括HCz模型和Hubbert模型。对于累积增长模型，提出了无因次典型曲线和拟合求解方法。通过无因次处理的油田实际开发数据与典型曲线的最佳拟合，可得到模型常数的数值，并用于对油田产量和可采储量的预测。实例应用表明，本文提供的累积增长预测模型典型曲线和拟合求解的方法是实用有效的。

累积增长预测模型；无因次典型曲线；拟合求解；油田产量；可采储量

由胡建国等建立的HCz模型［1］和由哈伯特建立的Hubbert模型［2］都属于累积增长预测模型，前者可以简化为国外的Moore模型［3］和国内的Compatz模型［4］，后者在国内又称为Logistic模型。本文对HCz模型和Hubbert模型进行了无因次化处理，提出了预测模型的无因次关系式，建立了预测模型典型曲线图版和拟合求解方法，并在拟合求解模型常数的基础上提出了预测油田产量、累积产量和可采储量的方法。实例应用表明，这些方法都是实用有效的。

1 HCz模型的典型曲线

1.1 HCZ模型的无因次化处理

HCz模型主要关系式为［1］

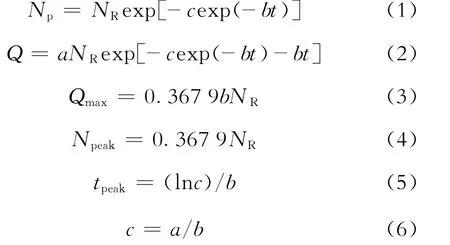
无因次累积产量和无因次时间分别由下式表示：

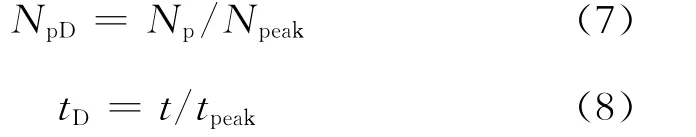
考虑到式（7）和式（8）的关系，由式（1）可得HCz模型的无因次关系式为

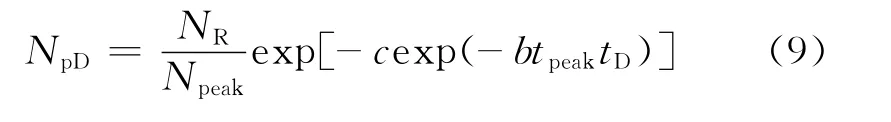
将式（3）和式（4）代入式（9），得HCz模型的无因次关系式为

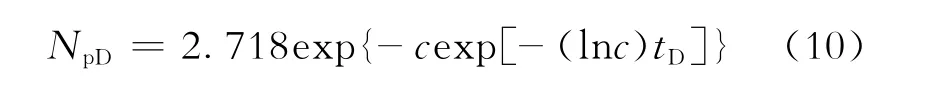
1.2 HCZ模型的典型曲线图版

给定不同的c值，由式（10）计算不同tD值对应的NpD值，由这些数值即可绘制HCz模型的典型曲线图版（图1）。

1.3 HCZ模型典型曲线的拟合求解

1）从油田的实际开发数据中找出Qmax、Npeak和tpeak的数值；

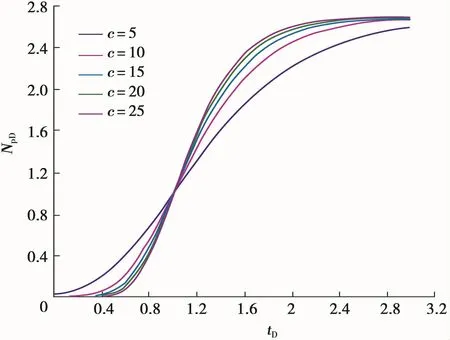
图1 HCZ模型的典型曲线

2）由式（7）和式（8）分别计算不同时间的NpD和tD的数值；

3）将NpD与tD的相应数值通过人工与典型曲线的印刷图版（图1）相拟合，或通过计算机与典型曲线的电子图版自动拟合，可直接得到该模型常数c的数值。

1.4 预测模型的累积产量、年产量和可采储量

在已知Qmax、Npeak、tpeak和c的数值条件下，由下面的公式分别预测油田的Np和Q的相应数值：

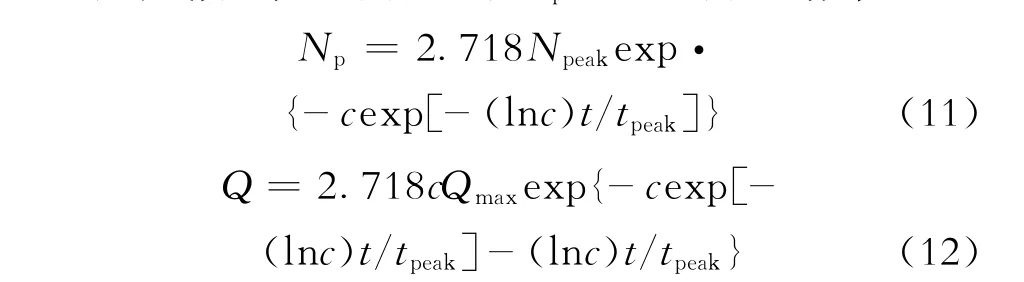
油田的可采储量可由式（4）改写的下式确定：

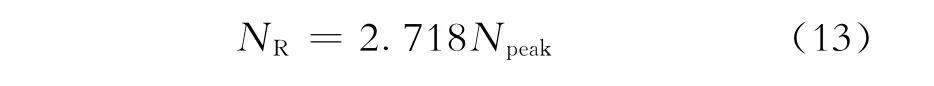
2 Hubbert模型的典型曲线

2.1 Hubbert模型的无因次化处理

哈伯特［2］于1962年利用逻辑推理的方法提出了预测油气资源量和储量的方法，后人称之为Hubbert模型。该模型于1984年由翁文波［5］引入我国，被称为Logistic模型。Hubbert模型于1996年由文献［6］完成了理论上的推导，比文献［7］的推导要早一年多。Hubbert模型的主要关系式为［6］

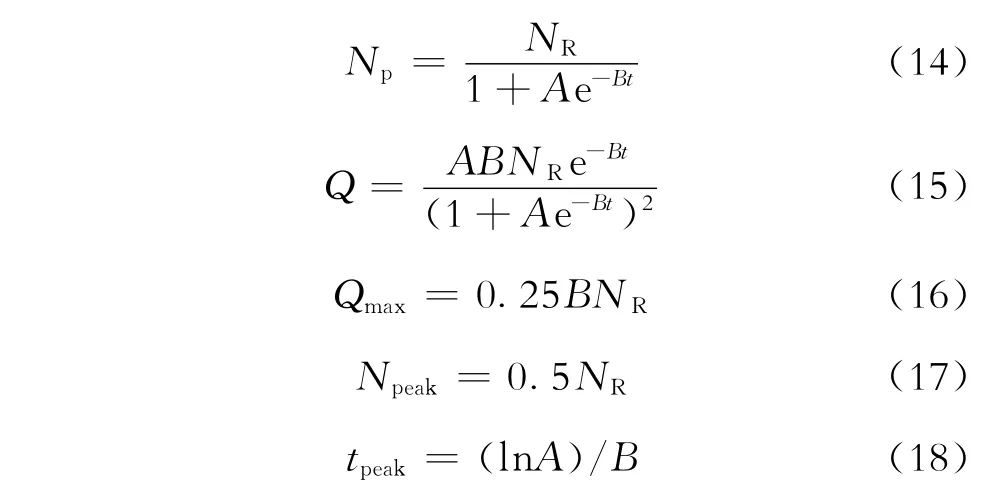
考虑到式（7）和式（8）的无因次关系，将式（14）改写为如下无因次形式：

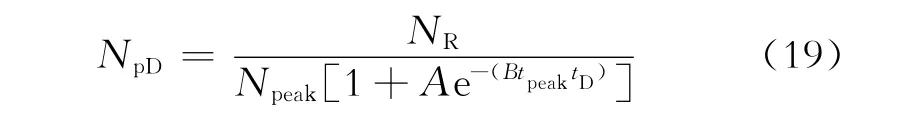
再将式（17）和式（18）代入式（19），得Hubbert模型的无因次关系式为

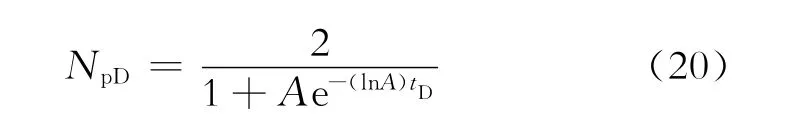
2.2 Hubbert模型的典型曲线图版

给定不同的A值，由式（20）计算不同tD值下的NpD值，由这些数值可以绘制Hubbert模型的典型曲线图版（图2）。

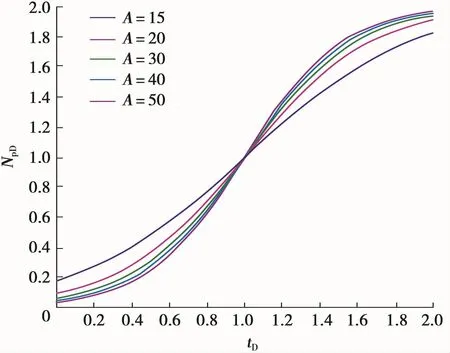
图2 Hubbert模型的典型曲线图版

2.3 Hubbert模型典型曲线的拟合求解

Hubbert模型典型曲线拟合求解的步骤与HCz模型典型曲线相同。由最佳拟合求得该模型常数A的数值。

2.4 预测油田的累积产量、年产量和可采储量

在已知A、Npeak和tpeak数值的条件下，考虑到式（7）和式（8）的关系可得到预测不同时间的累积产量公式为

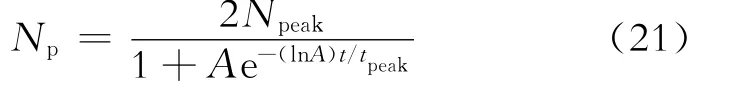
将式（15）改写为下式，并考虑式（8）的关系，可得到预测不同时间的年产量公式为

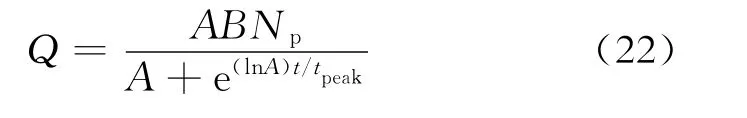
式（22）中的B值可由式（16）除以式（17）得到

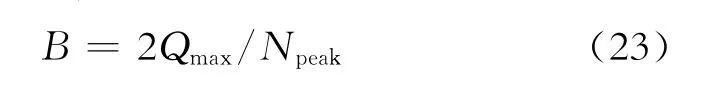
油田的可采储量可由式（17）改写的下式确定：

3 实例应用

下面通过两个实例来说明本文提出的HCz模型和Hubbert模型典型曲线的应用效果。

3.1 HCZ模型典型曲线的应用

俄罗斯萨马特洛尔油田在1969年至1990年间的开发数据列于表1，其特征生产数据为Qmax＝15 480万t／a，Npeak＝91 300万t，tpeak＝12 a。由式（7）和式（8）计算的NpD和tD的数值也列于表1。

利用HCz模型典型曲线的自动拟合求解方法，得到最佳拟合的c＝7.6（图3）。

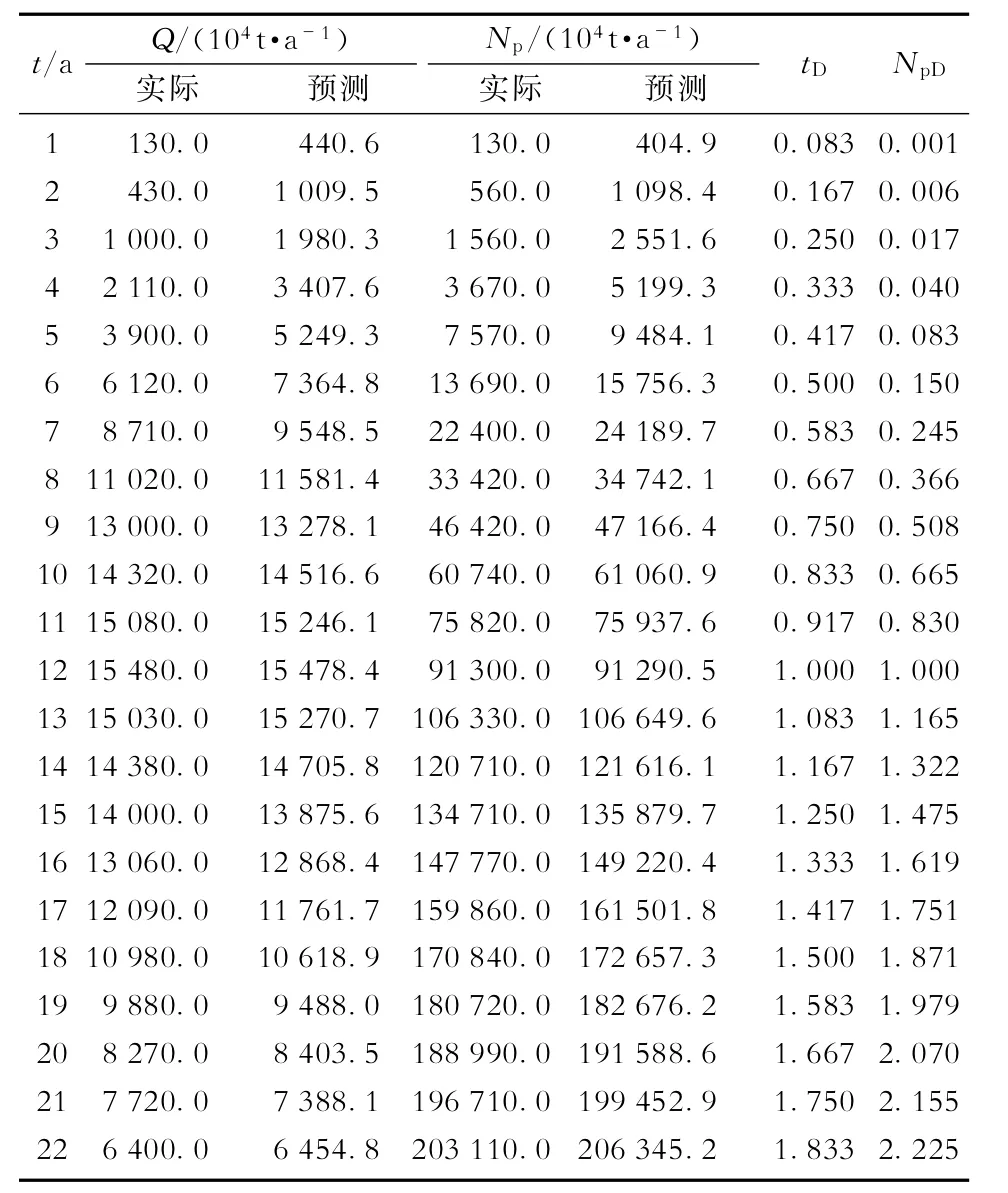
表1 萨马特洛尔油田的开发数据［8-9］

将c、Npeak、Qmax和tpeak的数值分别代入式（11）和式（12），得到预测油田不同开发时间产量和累积产量的公式为

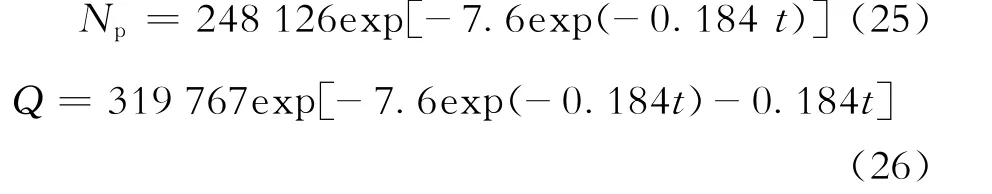
由式（25）和式（26）预测的结果列于表1。由表1可以看出，预测值和实际值非常接近。

将Npeak的数值代入式（13），得到油田的可采储量为

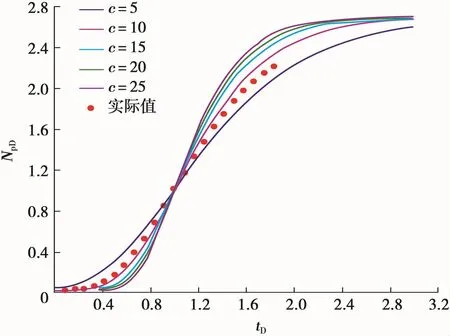
图3 萨马特洛尔油田最佳拟合图

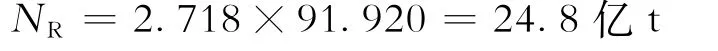
3.2 Hubbert典型曲线的应用

俄罗斯罗马什金油田在1953年至1982年间的油气当量开发数据列于表2，其特征生产数据为Qmax＝9 516万m3／a，Npeak＝112 076万m3，tpeak＝20 a。由式（7）和式（8）计算的tD和NpD的数值也列于表2。利用表2中的tD和NpD的相应数据与Hubbert典型曲线图版自动拟合，得到最佳拟合的A＝30（图4）。

将Qmax和Npeak的数值代入式（23），得到模型常数B的数值为B＝2×9 516／112 076＝0.17。

将A、B、Npeak和tpeak的数值代入式（21），得到预测不同时间Np数值的公式为

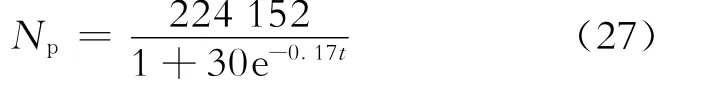
将A、B和tpeak的数值代入式（22），得到预测不

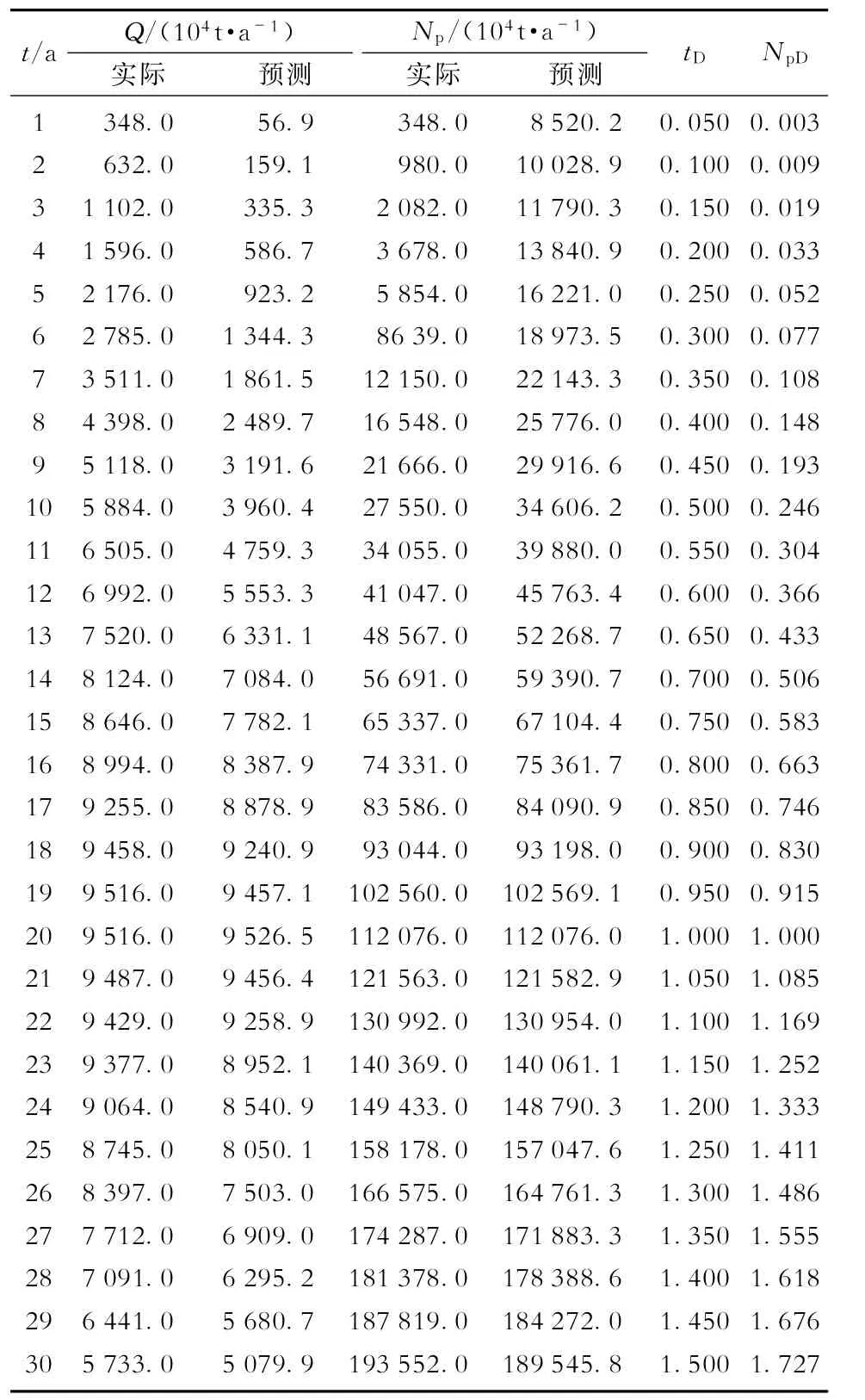
表2 罗马什金油田的开发数据［10-11］

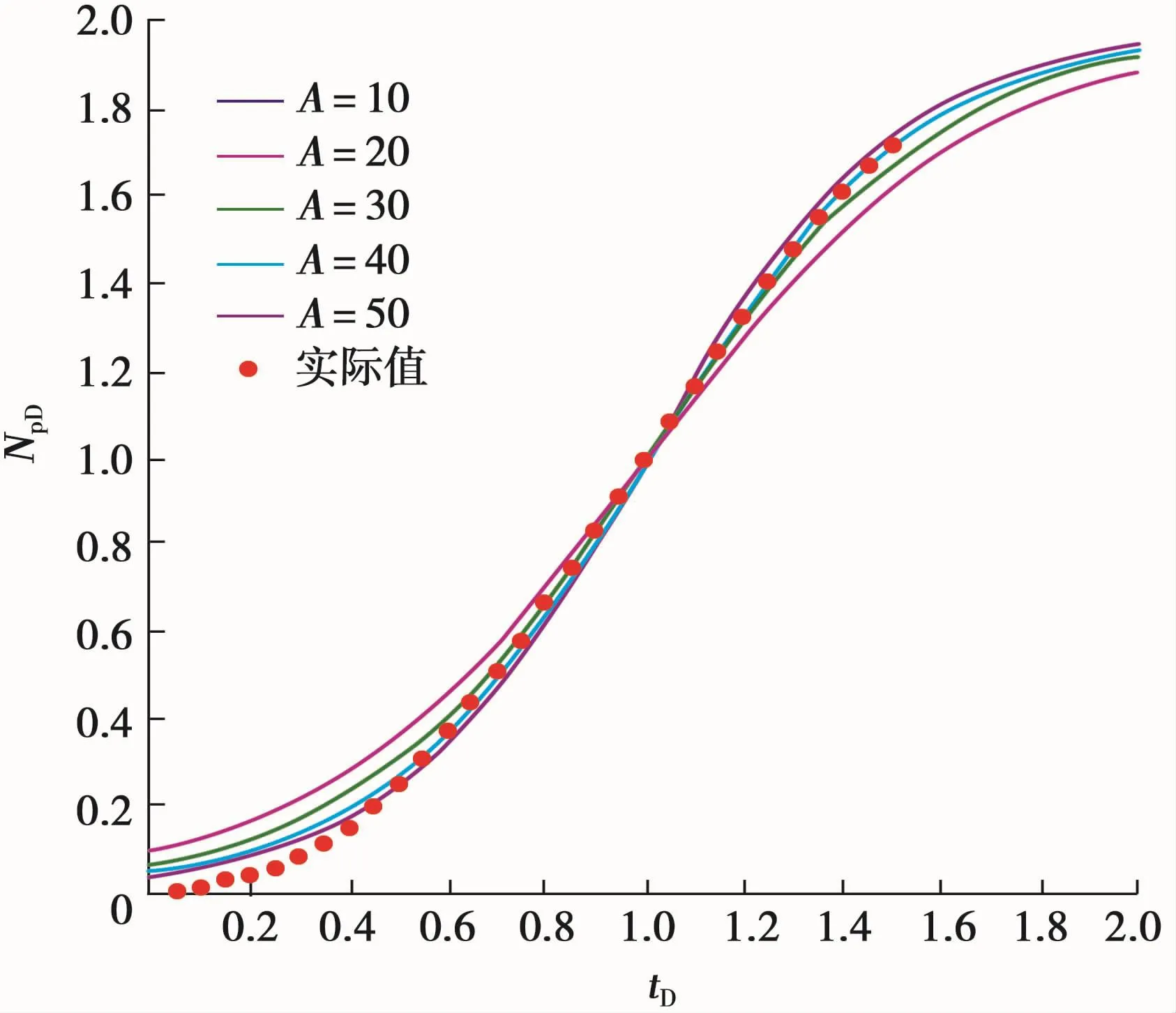
图4 罗马什金油田的最佳拟合图

同生产时间和相应Np数值下的年产量公式为

由式（27）和式（28）预测不同开发时间的累积产量和年产量数值也列于表2。由表2可以看出，预测值和实际值非常接近。

将Npeak的数值代入式（24），得到油田的可采储量为NR＝2×112 076＝22.4亿m3。

4 结束语

两个实例的应用结果表明，本文提出的累积增长预测模型的典型曲线是实用有效的。累积增长预测模型所预测的累积产量要比年产量更为接近实际。从理论上讲，由于Hubbert模型是一个钟形对称、峰位要采出50%的可采储量，因此该模型的实用性要较HCz模型差一些。应当指出，无论是单峰周期模型，还是累积增长模型，对于一个具体油田来说，在应用时都存在一个模型适应性的选择问题，预测值与实际值符合较好是选择的前提。本文提出的累积增长预测模型典型曲线和自动拟合求解方法，可以用于由文献［12，13］提供的多峰预测模型。

符号注释

Q—油田年产量，104t／a或104m3／a；Qmax—最高年产量，104t／a或104m3／a；t—生产时间，a；tD—无因次时间；tpeak—与Qmax相应的峰值时间，a；Np—累积产量，104t或104m3；NpD—无因次累积产量；Npeak—与Qmax相应的累积产量，104t或104m3；NR—可采储量，104t或104m3；a、b和c—HCz模型常数；A和B—Hubbert模型常数；exp（－x）＝e－x—指数函数。

［1］ 胡建国，陈元千，张盛宗．预测油气田产量的新模型［J］．石油学报，1995，16（1）：79-86．

［2］ HUBBERT，M K．Energy Resources［R］．Washington D C：National Academy of Sciences，National Research Council，1962．

［3］ 刘泉海．油气田可采储量的简便预测方法［J］．石油勘探与开发，1996，23（6）：71-72．

［4］ 陈玉祥，张汉亚．预测技术与应用［M］．北京：机械工业出版社，1985．

［5］ 翁文波．预测论基础［M］．北京：石油工业出版社，1984．

［6］ 陈元千，胡建国，张栋杰．Logistic模型的推导及自回归方法［J］．新疆石油地质，1996，17（2）：150-155．

［7］ AL-JARRI A S，STARTz MAN R A．Worldwide petroleumliquid supply and demand［J］．Journal of Petroleum Technology，1997，49（12）：1329-1338．

［8］ 陈元千．油气藏工程实践［M］．北京：石油工业出版社，2005：415-424．

［9］ 陈元千，赵庆飞．预测油气田剩余可采储量和储采化的方法［J］．中国海上油气，2005，17（4）：242-244．

［10］ 彭仕宓，陈元千．实用油气田开发地质与油藏工程方法［M］．北京：石油工业出版社，2013：332-338．

［11］ 陈元千，郭二鹏．新型油田产量递减模型的建立与应用［J］．中国海上油气，2008，20（6）：379-381．

［12］ 陈元千，郝明强．多峰预测模型的建立与应用［J］．新疆石油地质，2013，34（3）：296-299．

［13］ 陈元千，郝明强．HCz模型在多峰预测中的应用［J］．石油学报，2013，34（4）：747-752．

A type curve of the cumulative growth forecast models and its application

Chen Yuanqian zou Cunyou Yu Lijun
（Research Institute of Petroleum Exploration& Development，PetroChina，Beijing，100083）

The forecast models can be divided into single-peak cycle models and cumulative growth models by the changes of oil production and cumulative oil production，with the former including Weng model，Weibull model，Reyleigh model，Chen-Hao model and the generalized model，and the latter including HCz model and Hubbert model．For the cumulative growth forecast models，a dimensionless type curve and match method were developed．By best matching between any dimensionless oilfield development data and the type curve，the model constant can be obtained and used to forecast production and recoverable reserves of oilfields．The practical applications have shown that this type curve and match method are feasible and effective．

cumulative growth forecast model；dimensionless type curve；match method；oilfield production；recoverable reserves

2013-10-09

（编辑：张喜林）

陈元千，男，教授级高级工程师，1952年考入清华大学采矿系，1956年毕业于原北京石油学院钻采系，长期从事油田开发、油气藏工程和油气储量评价等方面的科研与实践工作。地址：北京市海淀区学院路20号（邮编：100083）。