基于模糊熵的核电站瞬态识别方法
常 远,郝 轶,黄晓津,李春文,梁记兴,刘景源
(1.清华大学 自动化系,北京 100084;2.大唐微电子技术有限公司,北京 100095; 3.清华大学 核能与新能源技术研究院,北京 100084;4.郑州轻工业学院 机电工程学院,河南 郑州 450000;5.中国原子能科学研究院,北京 102413)
核电站是一类对安全性要求极高的复杂系统,通常由操纵员进行监控并有多种故障诊断方法为其提供辅助支持[1],而在故障发生的早期做出正确判断会更有利于保证核电站安全[2-3]。近年发展的瞬态识别技术可及时为操纵员提供发展中的故障信息,及时采取合适的操作动作,可避免出现故障或降低系统受到的影响[2,4-5]。这对已长期在役[6]和缺乏运行经验的新堆型的安全稳定运行均具有重要意义[7]。
核电站中的瞬态识别一般是针对由异常事件或故障所引起的瞬态过程[2,6-7]。由于典型的瞬态过程会引起相关的变量以特定的趋势演化[6,8],可据此特性识别初因事件[2],这属于模式分类问题[6-7]。当前,核电站的瞬态识别大部分基于神经网络方法[6],而某些神经网络的训练过程较为复杂[2,4-5]。除此之外,也有部分采用统计方法[6],如隐马尔科夫模型(HMM)[8]和支持向量机(SVM)[9-10]。前者为每类瞬态过程训练1个HMM,训练过程较慢[8]。SVM是一种很好的分类器,尤其有利于小样本应用,但仍有核函数的选择和参数的优化等问题待解决[9]。
实际上,表征瞬态过程的变量往往经过采样,以时间序列的形式记录和显示。通过分析该时间序列,可确定系统状态。本文采用模糊熵和互模糊熵这两个统计量进行瞬态识别,利用模块式高温气冷堆核电站(HTR-PM)仿真机的故障数据对该方法进行有效性验证。
1 用于时间序列分析的模糊熵与互模糊熵
Pincus等[11]提出了近似熵以度量生理学时间序列的复杂度,适用于包含噪声的较短数据的分析,但相对一致性较差。Richman等[12]提出样本熵,通过排除与自身的比较来减小偏差并提高相对一致性,但其采用二值分类器对嵌入向量进行比较,结果的波动较大。Chen等[13]进一步结合模糊理论提出模糊熵,得到比前两种度量更准确的结果,并具有更好的相对一致性[14]。
对于长度为N的时间序列y={y(1),y(2),…,y(N)},其模糊熵可根据文献[13-14]按如下步骤求得:
1) 设嵌入维度为m,生成N-m+1个向量{Y(1),Y(2),…,Y(N-m+1)},其中:
Y(i)={y(i),y(i+1),…,y(i+m-1)}
1≤i≤N-m+1
(1)
这里Y(i)的构造与文献[13-14]中稍有不同。文献[13-14]在式(1)的基础上减去{y(i),y(i+1),…,y(i+m-1)}的均值y0(i),而验证发现,本文的应用中采用式(1)具有更好的效果。
2) 定义Y(i)和Y(j)之间的距离d[Y(i),Y(j)]为二者对应元素之差的绝对值中的最大值:

(2)
3) 利用指数函数定义在给定参数n和r下Y(i)和Y(j)之间的相似度:
(3)
4) 定义函数φm:
(4)
5) 增加嵌入维度为m+1,按照步骤1~4得到函数φm+1:
(5)
6) 最后,对于有限长度的数据,定义模糊熵为:
FuzzyEn(m,n,r,N)=
lnφm(n,r)-lnφm+1(n,r)
(6)
为度量两个时间序列的相似度,Xie等[15]提出了互模糊熵,是模糊熵的推广,其定义和计算过程与模糊熵相似。对于给定的两个时间序列z={z(1),z(2),…,z(N)}和y={y(1),y(2),…,y(N)},按照式(1)分别构造m维的嵌入向量:{Z(1),Z(2),…,Z(N-m+1)}和{Y(1),Y(2),…,Y(N-m+1)}。将Z(i)和Y(j)之间的距离d[Z(i),Y(j)]定义为其对应元素之差的最大绝对值:
z0(i)-y(j+k)+y0(j)|
(7)
而之后的计算步骤与计算模糊熵的步骤3~6相同。
可见,对于给定长度的时间序列,模糊熵与互模糊熵均与m、n和r的取值有关。n和r的取值决定了式(3)中指数函数的形状[13],通常容限误差取r=(0.1~0.25)Std,其中Std为时间序列的方差,n取大于1的小整数[14-15]。嵌入维度通常为m=1或2,而为得到较为稳定的解,需要满足N≥10m~30m。这样处理较适合核电站的瞬态识别问题,因为其可能演化较快而具有较短的数据长度[2]。为方便起见,分别用S和xS表示1个时间序列的模糊熵和两个时间序列之间的互模糊熵。
2 基于模糊熵的瞬态识别方法
2.1 利用模糊熵区分正常与瞬态过程
核电站中瞬态过程与正常状态具有不同的演化特性,因而可通过它们的模糊熵数值加以区分。通常认为,瞬态发生时,相关变量将以特定的趋势演化[2,8],而正常状态的变量往往在稳定值附近波动,可利用带有随机噪声的恒定值进行模拟。直观上,正常状态比瞬态过程较为规则。但在进行时间序列的熵分析时,往往利用(y-y0)/std(y)进行标准化[11-12],其中y0表示y的均值,std(y)为y的标准差。此时,瞬态过程仍能保持其趋势特征,而正常状态的数据点就主要受到噪声等扰动的影响。通常认为噪声具有较大的复杂度和不规则度[14],从而具有较大的模糊熵。
若模糊熵的数值大幅度降低,则可能出现了瞬态过程,需及时进行诊断识别。不同的瞬态过程表现出不同数值的模糊熵,但区别不够明显。因此,选择互模糊熵识别瞬态过程的具体类型。
2.2 基于互模糊熵的瞬态识别
通过计算在线瞬态过程与参考数据的互模糊熵,最小的数值意味着最大的相似性,可据此进行类型识别。假设有c个参考类别,均由d个变量表征,如果每个变量有s个数据点,则1个瞬态过程可表示为:
(8)
其中:{v1,v2,…,vd}为状态变量;vd(s)为vd的第s个数据点。
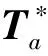
(9)
其中,xS[x,y]为x和y之间的互模糊熵。
利用式(8)和(9)进行计算,只能比较某一时刻的互模糊熵,无法持续一段时间且易受到扰动影响。为能将在线过程与更多的参考数据进行匹配比较,可对数据截取一系列长度为k(1≤k≤s)的向量。以vd为例,构造瞬态向量{Xd(1),Xd(2),…,Xd(s-k+1)},其中Xd(γ)按下式[7]得到:
Xd(γ)=[vd(γ),vd(γ+1),…,vd(γ+k-1)]T
γ=1,2,…,s-k+1
(10)
利用新生成的向量,在线数据与参考向量之间的平均模糊熵可定义为:
(11)

如果有最小值xSmin={xSa,mean},则可将当前的待识别瞬态过程归为其对应的类别。
式(11)利用生成的s-k+1个向量进行计算,具有较好的鲁棒性,但需计算dk(s-k+1)次互模糊熵。实际上可能只需与w个向量进行计算即可,则式(11)可改为:
(12)
其中,wi用来指示参与计算的起始参考向量,宽度为w个向量的窗口随时间而向后移动。此时只需计算dkw次互模糊熵,可在一定程度上提高计算效率。
3 验证与讨论
利用从清华大学的HTR-PM仿真机[7]中提取的故障瞬态数据(表1)验证本文方法。所使用的9个瞬态过程来自3个故障类,且同一类的数据可能来自不同工况。将其分为2组:T2~T7作为参考数据,而T8~T10用作验证。为方便起见,将正常状态作为T1与以上数据列在一起。选择4个关键变量表征:反应堆堆芯热功率、入口氦气温度、出口氦气温度和二回路给水流量。数据带有±1%的高斯白噪声,采样周期为1 s,每个变量150个采样点,且瞬态过程从第36 s开始。
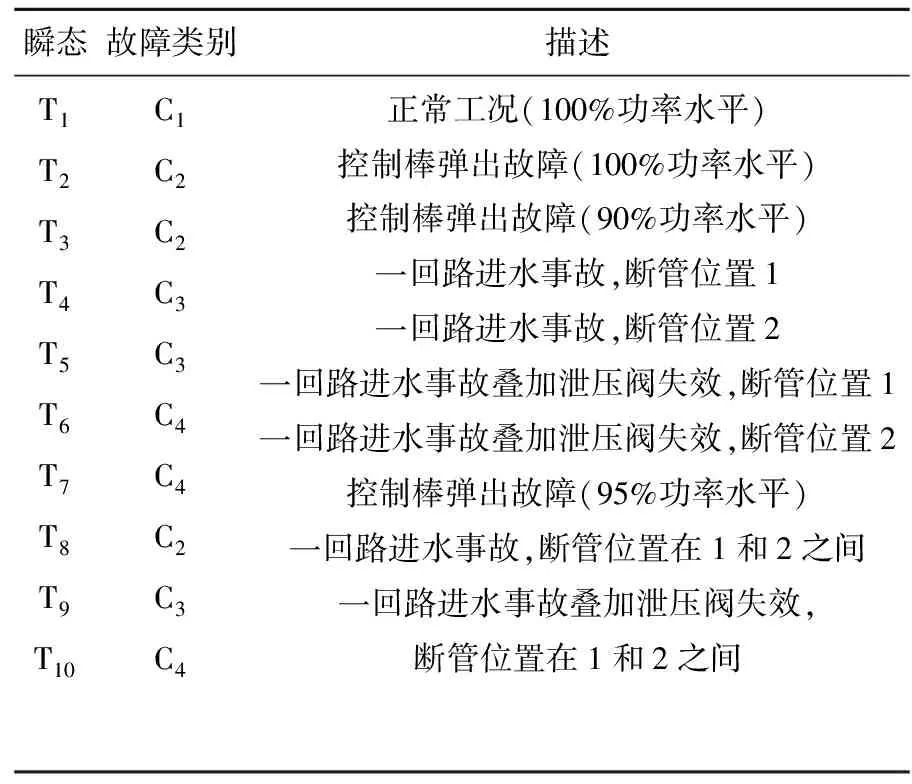
表1 HTR-PM故障瞬态过程
参数设置为n=2,r=0.1Std[13-15],式(10)中构造向量的长度k=41,即为计算模糊熵和互模糊熵的数据长度N,而为满足N≥10m~30m,确定m=1。经过(y-y0)/std(y)进行标准化[11-12]之后,正常工况的数据比瞬态过程复杂、不规则,具有更大的模糊熵,如图1所示。据此可判断系统的正常与异常状态。当系统模糊熵持续下降时可能出现瞬态,而考虑扰动的影响,可在小于某一阈值(本文为0.8)时开始互模糊熵的计算。
利用参考组瞬态过程T2~T7的向量进行测试,结果如图2所示。而验证组瞬态过程T8~T10的测试结果如图3a~c所示。可见,这两种情况均可正确地识别和分类,识别率均为100%。
以上测试过程利用了每个瞬态过程构造的所有110个瞬态向量,使得在线数据的每个循环(与T2~T7计算互模糊熵)平均耗时3.618 s。为提高计算速度,采用式(12),取w=25,保证在1个采样周期内完成识别计算。图3d~f为测试组数据与窗口中25个向量求平均互模糊熵的结果。随着窗口的移动,对每个瞬态进行86次计算和比较,每个循环平均计算时间为0.807 s。此时识别准确率稍有下降,如图3e中有11个错误识别情况,正确率为95.74%,但仍较高。且识别错误主要在尾部(第76个向量之后),之前的正确识别部分已及时提供信息。
由以上验证结果可见,本文方法可有效进行瞬态识别,且不需复杂的训练过程。在瞬态发生的第6 s发现并进行准确识别,可及时提供相关信息。

a——瞬态过程T1~T7的模糊熵;b——T1~T7所构造向量的模糊熵,Sx表示Tx的模糊熵 ◆——S1;●——S2;■——S3;▲——S4;▼——S5;▶——S6;◀——S7
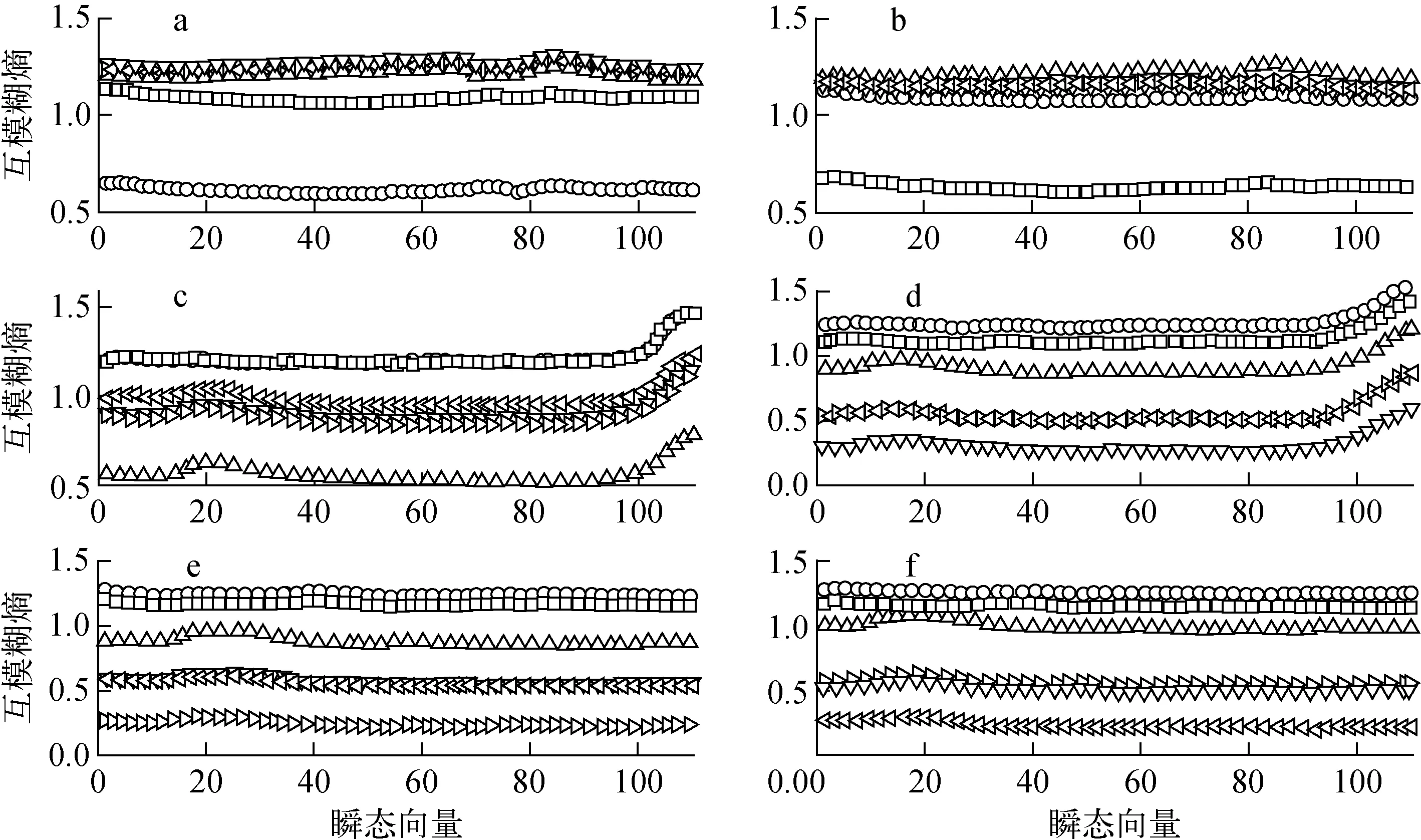
a~f分别为T2~T7与参考向量的互模糊熵,xSx表示在线数据与Tx的互模糊熵 ○——xS2;□——xS3;△——xS4;▽——xS5;▷——xS6;◁——xS7
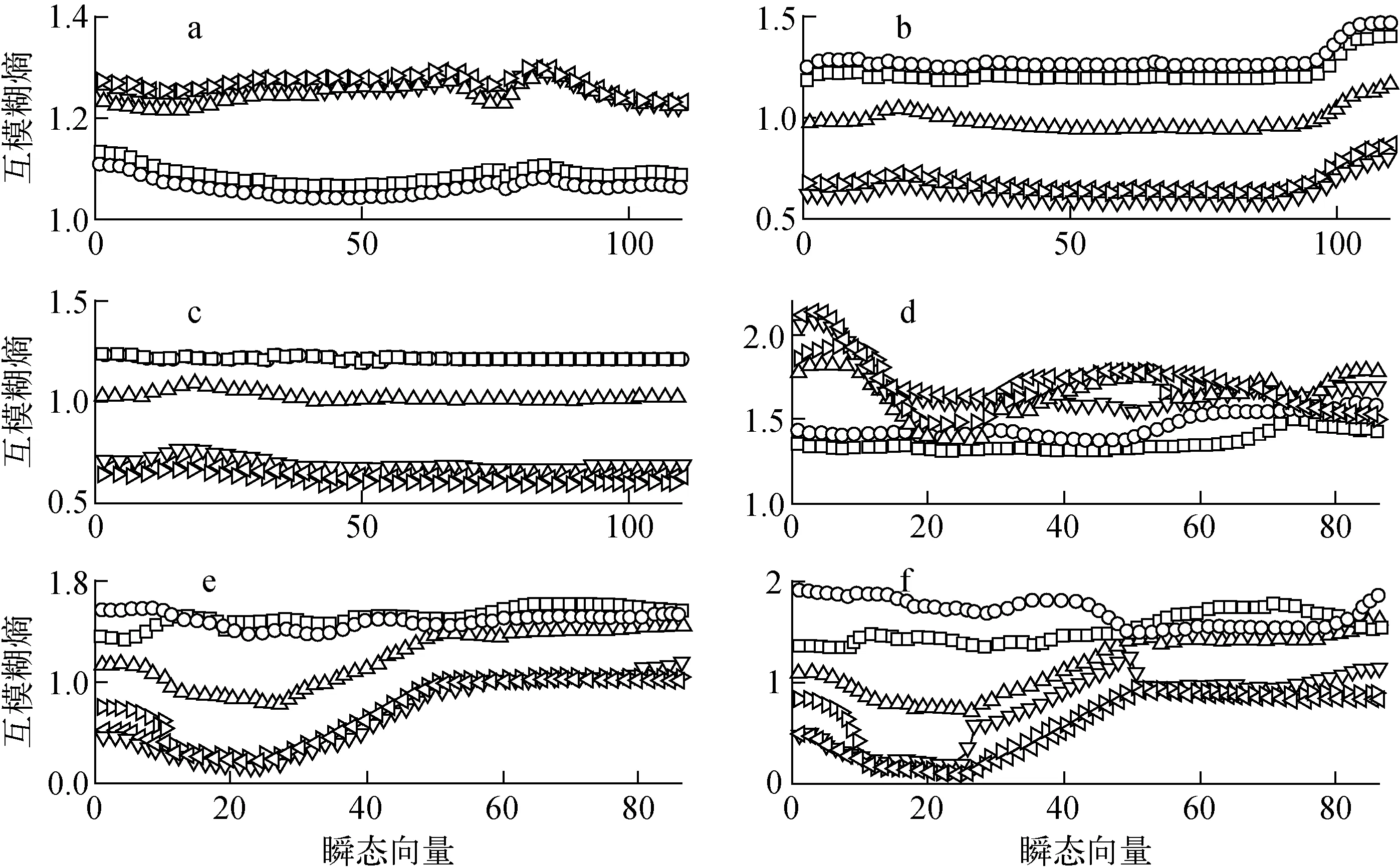
a~c——利用110个参考向量的互模糊熵;d~f——利用w=25个参考向量的互模糊熵 ○——xS2;□——xS3;△——xS4;▽——xS5;▷——xS6;◁——xS7
4 结束语
核电站的瞬态识别可发现处于发展阶段的异常状况,及时为操纵员提供诊断信息,从而提高核电站运行的安全性和经济性。本文利用模糊熵表征时间序列复杂度的特性识别系统的正常与异常状态,当其下降到阈值以下时,通过计算在线数据与参考瞬态向量的互模糊熵,根据最小值进行识别和分类。利用HTR-PM仿真机的故障数据,验证了该方法的有效性。
参考文献:
[1]MA J, JIANG J. Applications of fault detection and diagnosis methods in nuclear power plant: A review[J]. Progress in Nuclear Energy, 2011, 53(3): 255-266.
[2]ROVERSO D. Plant diagnostics by transient classification: The ALADDIN approach[J]. International Journal of Intelligent Systems, 2002, 17(8): 767-790.
[3]NO Y G, KIM J H, NA M G, et al. Monitoring severe accidents using AI techniques[J]. Nuclear Engineering and Technology, 2012, 44(4): 393-404.
[4]SANTOSH T V, VINOD G, SARAF R K, et al. Application of artificial neural networks to nuclear power plant transient diagnosis[J]. Reliability Engineering & System Safety, 2007, 92(10): 1 468-1 472.
[5]SANTOSH T V, SRIVASTAVA A, SANYASIRAO V V S, et al. Diagnostic system for identification of accident scenarios in nuclear power plants using artificial neural networks[J]. Reliability Engineering & System Safety, 2009, 94(3): 759-762.
[6]MOSHKBAR-BAKHSHAYESH K, GHOFRANI M B. Transient identification in nuclear power plants: A review[J]. Progress in Nuclear Energy, 2013, 67: 23-32.
[7]CHANG Y, HUANG X, HAO Y, et al. Linear representation and sparse solution for transient identification in nuclear power plants[J]. IEEE Transactions on Nuclear Science, 2013, 60(1): 319-327.
[8]KWON K, KIM J, SEONG P. Hidden Markov model-based real-time transient identifications in nuclear power plants[J]. International Journal of Intelligent Systems, 2002, 17: 791-811.
[9]GOTTLIEB C, ARZHANOV V, GUDOWSKI W, et al. Feasibility study on transient identification in nuclear power plants using support vector machines[J]. Nuclear Technology, 2006, 155(1): 67-77.
[10] GOTTLIEB C, GARIS N. 基于SVM的核电厂瞬态识别可行性研究[J]. 毛辉辉,译. 国外核动力,2007,28(1):12-64.
[11] PINCUS S M, GOLDBERGER A L. Physiological time-series analysis: What does regularity quantify?[J]. American Journal of Physiology-Heart and Circulatory Physiology, 1994, 266(4): H1643-H1656.
[12] RICHMAN J S, MOORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278(6): H2039-H2049.
[13] CHEN W, WANG Z, XIE H, et al. Characterization of surface EMG signal based on fuzzy entropy[J]. Neural Systems and Rehabilitation Engineering, IEEE Transactions on, 2007, 15(2): 266-272.
[14] CHEN W, ZHUANG J, YU W, et al. Measuring complexity using FuzzyEn, ApEn, and SampEn[J]. Medical Engineering & Physics, 2009, 31(1): 61-68.
[15] XIE H B, ZHENG Y P, GUO J Y, et al. Cross-fuzzy entropy: A new method to test pattern synchrony of bivariate time series[J]. Information Sciences, 2010, 180(9): 1 715-1 724.

