C型换热器管外流体两相自然循环数值模拟

陈 薇，王 盟，丁铜伟

(1.国核(北京)科学技术研究院有限公司，北京 100029；2.国家国防科技工业局 核技术支持中心，北京 100037)

第三代核电站的一个显著特点是广泛采用非能动安全系统，非能动安全系统的应用可有效降低堆芯熔毁概率和放射性物质泄漏，提高了系统运行的可靠性[1]。非能动余热排出换热器是其中的关键设备，其换热性能直接关系到整个系统的安全性和紧凑性。非能动余热排出换热器通常浸没在大容积冷却水池内，通过与管外流体的对流换热导出反应堆衰变热。系统刚启动时，大容积冷却水池内流体过冷度较大，换热管外侧为单相对流换热，随冷却水温度的升高，换热管外侧转变为过冷沸腾直至饱和沸腾。

换热器管外流体运动特性复杂，借助CFD手段捕捉管外流体运动特性，可为非能动余热排出换热器的设计提供支持。薛若军等[2]用FLUENT软件研究了管外流体单相自然对流换热，但对于两相自然循环，由于涉及到过冷沸腾等复杂现象，CFD程序的适用性有待进一步验证，C型等复杂结构换热器管外流体两相自然循环特性的研究也几乎未开展。

本文建立C型换热器管外流体简化分析模型，模拟反应堆安全壳内置换料水箱(IRWST)冷却水池中典型的两相自然循环特征，计算结果可为非能动余热排出换热器的设计提供支持。

1 数值方法[3-4]

本研究的难点是如何模拟大容积冷却水池内的沸腾特性。目前，壁面热流分配模型(RPI)已成功用于流动条件下过冷沸腾模拟，如竖直环管内过冷沸腾现象[5]、反应堆燃料组件CHF预测[6]等。本研究首先验证数值计算方法对大容积水池内两相自然循环的适用性。

1.1 壁面热流分配模型

过冷沸腾时，壁面上的热流密度qw可分为3部分：单相对流换热热流密度qc、骤冷热流密度qq、蒸发热流密度qe，即：

qw=qq+qe+qc

(1)

其中：

qc=hcAl(Tw-Tf)

(2)

式中：Tw为壁面温度，K；Tf为流体温度，K；Al为壁面上液相所占份额；hc为单相对流换热系数，hc=Stρfcpfuf，W/(m2·K)，St为局部Stanton数，St=Nu/PrRe，Pr为液体普朗特数，uf为近壁面第1个控制体内与加热面平行的流体速度，cpf为液相比定压热容，J/(kg-1·K)。

(3)

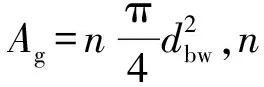
(4)

式中：hsat为饱和气体焓，J/(kg·K)；hf为液体焓，J/(kg·K)

1.2 相间力模型

(5)

其中，曳力为：

被解释变量：选取企业的总税负率作为衡量企业总税负的指标，选取销售利润率(又称为净利润率)作为衡量企业盈利能力的指标。

(6)

式中：CD为曳力系数，由经验关系式确定；α为空泡份额；Ug、Uf分别为气体和液体速度，m/s。

升力为：

(7)

ωf=curlUf

(8)

式中，CL为升力系数。

湍流耗散力为：

(9)

式中：nw为壁面法向量；CWL为壁面润滑力系数，由经验关系式确定。

壁面润滑力为：

(10)

1.3 相间传热模型

采用Ranz-Marshall模型计算主流流体间气液两相间换热：

(11)

式中：k∞为液体导热系数，W/(m·K)；Red为气体雷诺数。

2 程序验证

用上述模型模拟大容积水池内气液两相自然循环特性，并将计算结果与Asdozi试验[7]对比，Asdozi试验为大容积水池加热试验。试验段圆柱形表面为加热面，加热功率随时间的变化示于图1，试验段直径为0.25 m，高为0.25 m，工质为水，初始水位高度为0.21 m。流体温度用热电偶测量，其中T12、T14、T17号热电偶沿水池轴线方向布置，与水池底部的距离分别为20、90及195 mm。

计算中将圆柱形试验段简化为二维切片结构，周向划分一层网格，两个对称的矩形面设置为旋转周期性边界条件。轴向划分50个网格，径向划分100个网格，第1层网格距壁面0.5 mm。选用两流体方程求解，两相工质分别为水和水蒸气，水为连续相、水蒸气为弥散相，连续相湍流模型选用SST模型，弥散相选用零方程求解，即弥散相随连续相运动，不单独求解动量方程。壁面热流密度根据试验参数拟合输入，出口定义为degassing边界条件，这类边界条件对气体和液体进行不同处理：对于气体，出口为outlet边界；对于液体，出口为wall边界，即允许气体溢出，而液体滞留在水池内。

相间作用力考虑曳力和非曳力，曳力选用Ishii模型，非曳力包括升力、壁面润滑力、湍流耗散力，分别选用Tomiyama、Antal、Favre模型。

加热过程中，流体升温特性曲线计算值与实验值对比如图2所示。从图2可看出，计算值与实验结果基本相同。大容积水池内流体升温过程可分为两个阶段，第一阶段为单相自然循环阶段，此时水池内流体温度较低，流体温度逐渐升高且呈现了明显的温度分层，水池上部流体升温速度高于水池下部流体升温速度。第二阶段为两相自然循环阶段，这一阶段流体升温特性与前一阶段明显不同，如在1 250 s左右，T12热电偶温度由330 K左右阶跃上升至饱和温度，这是因为加热壁面产生气泡后，两相自然循环能力增强，水箱内流体搅混剧烈，导致温度阶跃上升。

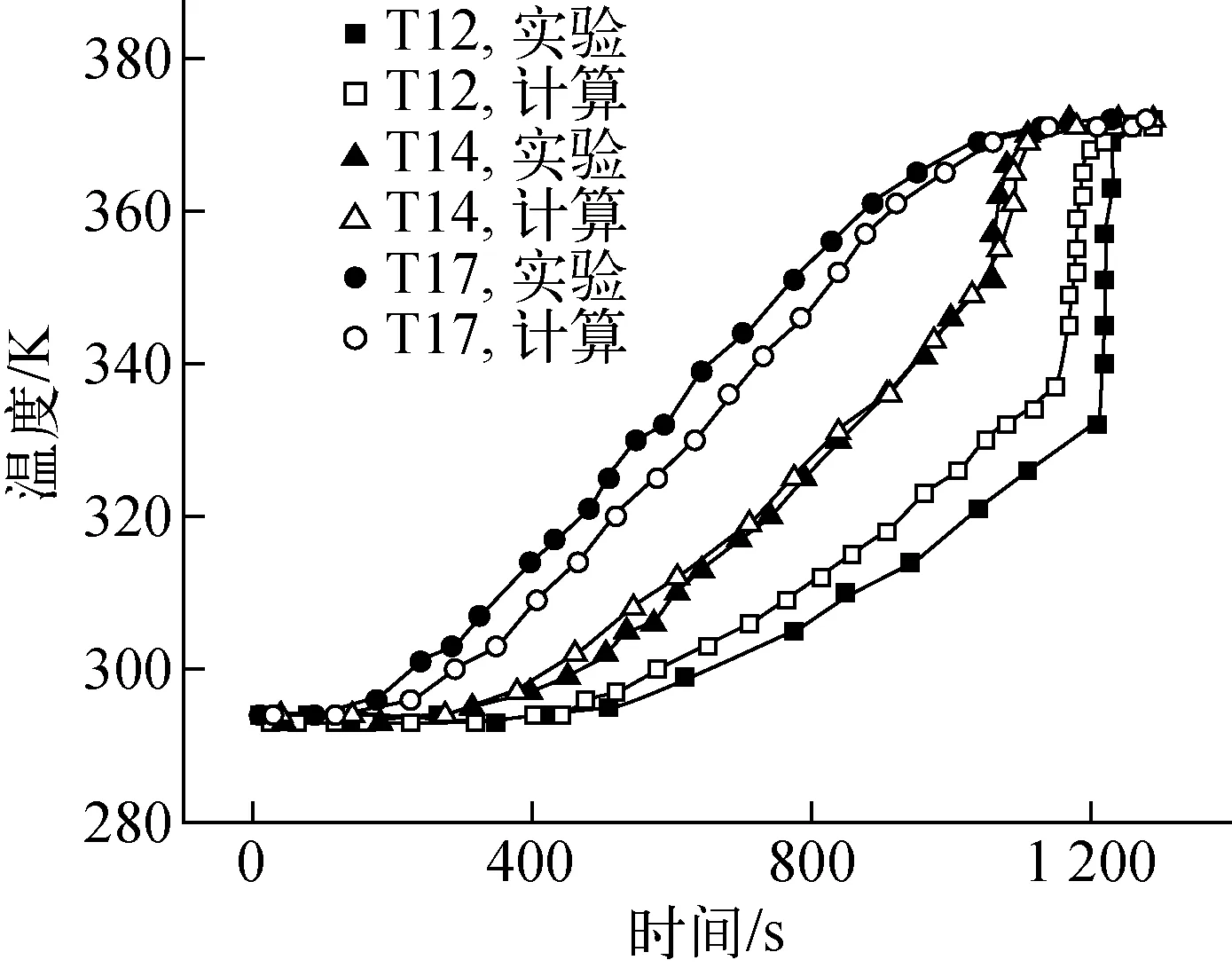
图2 升温过程中流体温度计算值与实验值的对比

从上述分析可知，计算中采用的过冷沸腾模型、湍流模型等能较好地模拟大容积水池内两相自然循环特性，这为后面分析C型换热器管外流体特性奠定了基础。

3 C型换热器管外流体流场分析

3.1 计算模型

AP1000 C型换热器有689根换热管，IRWST水体积可达2 092 m3，由于本文重点关注C型换热器管外流体典型流动、传热特征，因此建立了简化的分析模型，如图3a所示。水池直径约0.24 m，高约0.23 m，内含1根C型换热管，换热管直径0.03 m。本文仅关注换热管外流体，将换热管壁面简化为定热流密度边界条件，如需计算实际条件，可考虑换热管内、外流体的耦合换热。采用结构化网格划分计算域，并对换热管近壁面区域、水池上部区域进行了加密处理。为方便说明水池内部流场特性，在计算域内设置了两个监测面，分别为Plane1和Plane2，监测面的位置如图3a所示。另外，建立了直管型换热器分析模型，用于对比分析，以便更好地反映C型换热器管外流体的运动特性，计算模型如图3b所示，换热管的布置位置与C型换热器的相同。

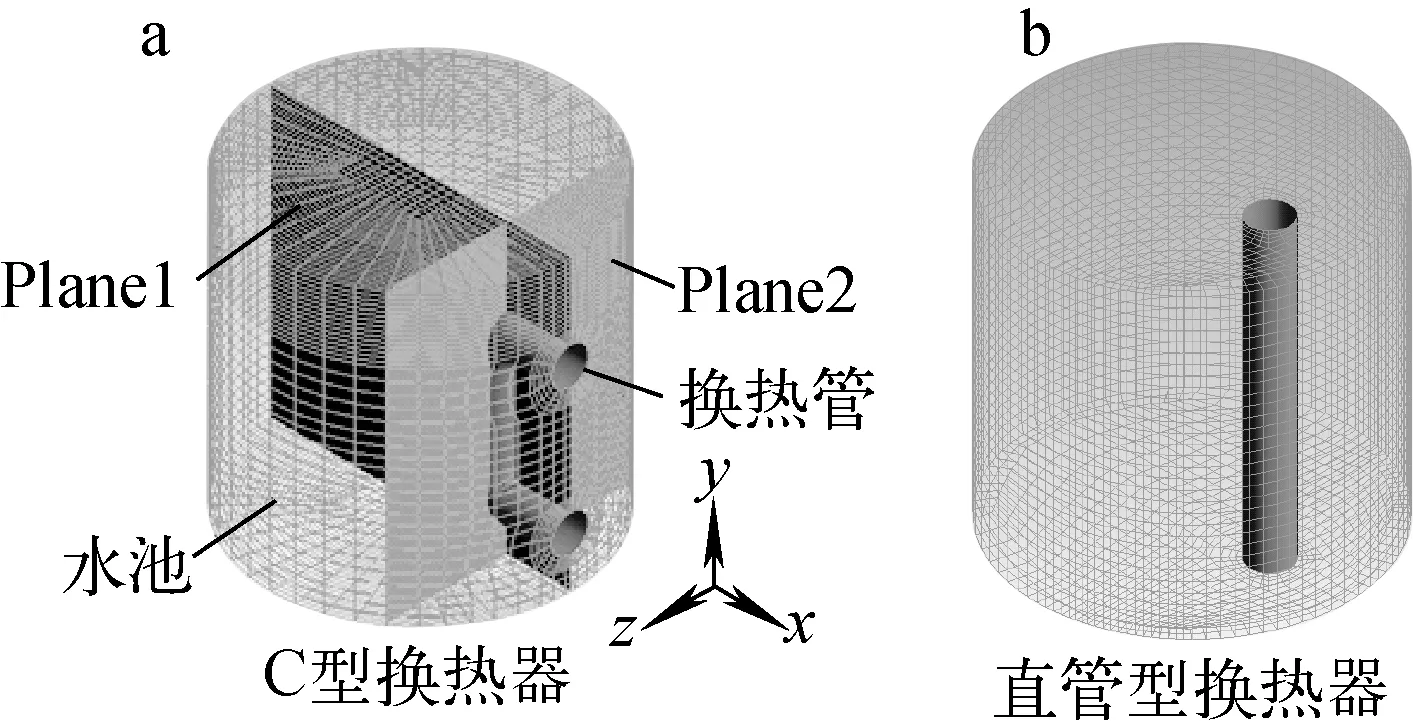
图3 管外流体计算模型

3.2 计算结果及分析

加热初始阶段，Plane1流体温度、速度分布如图4所示。加热初始阶段，有两个区域内流体温度最先升高，一个为水平管上方区域，另一个为被C型换热管包围区域。在浮升力作用下，高温流体向上流动，并聚集在水池顶部，因此水平管上方流体温度最先升高，且温升速度较快。对比速度分布图可发现，流体沿着竖直管壁向上运动，并顺着换热管弯管弧度方向发展，在水平管上方流速达到最大，随后向水池内非加热区扩展，高温流体也随着向外扩展。被C型换热管包围区域，由于加热面较多，流体温度较高，在重位压差作用下，产生局部循环流动。

加热中期，Plane2流体温度、速度分布如图5所示。随加热时间的增加，流体温度上升，水池内出现温度分层，且由于温差加大，流体速度也增加。换热管弯头附近流体速度最大，这是因为该部分流体温度较高，管壁对流动也无阻滞作用。水池上部及换热管弯头附近由于扰动剧烈，流体温度基本相同。

加热后期，Plane1空泡份额、流体速度如图6所示。加热后期，水池上方流体接近于饱和，开始沸腾并产生气泡，与初始阶段升温特性类似，气泡最先产生在水平管上方及被C型换热器包围的两个区域，且水平管上方气泡较多。沿着换热管弯头向上，流体受到的浮力较大，速度也较大，由于速度分布不均，导致水平管上方空泡份额分布呈波动状态。被C型换热器包围区域，换热管弯头及水平管下方局部位置上的空泡份额最大，这是因为壁面的滞止作用导致气泡难以脱离，从而发生了气泡聚集。产生气体后，管外流体由单相自然循环过渡到两相自然循环，循环能力显著提高。

图4 C型管外流体加热初始阶段温度和速度分布

图5 C型管外流体加热中期温度和速度分布

图6 C型管外流体加热后期温度和速度分布

3.3 与直管型换热器的对比

为更好地反映C型换热器管外流动特征，本文同时分析了直管型换热器，计算中直管型换热器的加热功率与C型换热器的相同。图7为t=90 s时，水池内温度、速度分布，此时大容积水池内为单相自然循环，流体温度在重力作用下形成了分层，速度分布较规则。

图8为t=300 s时，水池内温度、速度分布。随加热时间的增长，水池上部流体温度达到饱和，加热壁面附近产生气体，由单相自然循环转变为两相自然循环，自然循环流速增加，且在加热水箱上部局部位置产生了较大的湍动涡流。

图9为C型及直管型换热器管外流体升温特性，其中Plane3、4、5、6分别距水池底部0.05、0.1、0.15及0.2 m。C型换热器管外流体温差低于直管型换热器的，如t=300 s时，监测面上C型换热器管外流体最大温差为13 K，直管型换热器管外流体最大温差约20 K，由此可见，C型换热器管外流体扰动更剧烈，流体混合更均匀。

图7 竖直管外流体加热初始阶段温度和速度分布

图8 竖直管外流体加热后期温度和速度分布

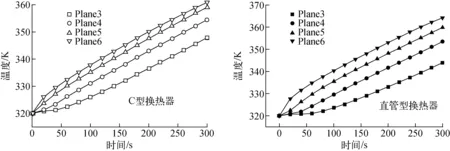
图9 C型及直管型换热器管外流体升温特性

由上述分析可知，直管型换热器管外流体运动特性较规则，C型换热器管外流体运动复杂，增加了冷、热流体之间的搅混，有助于增强换热器的换热能力。

4 结论

本文以公开发表的试验数据验证了CFX程序分析大容积冷却水池内两相自然循环特性的可行性，在此基础之上，分析了C型换热器管外流体由单相过渡到两相自然循环的典型现象，计算结果可为AP1000型反应堆换热器的设计及布置提供参考。得到的主要结论如下：

1) Asdozi试验的计算结果与试验结果符合较好，证明了CFX程序能较好地模拟大容积冷却水池内两相自然循环特性；

2) C型换热器水平管上方流体温度最高且最先发生沸腾，空泡份额的分布与速度有关，呈波动状态；

3) 与直管型换热器相比，C型换热器增加了管外流体流动的复杂程度，有助于增加管外冷、热流体之间的搅混，提高换热能力。

参考文献：

[1]李勇. 非能动余热排出换热器特性研究[D]. 哈尔滨：哈尔滨工程大学,2011.

[2]薛若军，邓程程，彭敏俊. 非能动余热排出热交换器数值模拟[J]. 原子能科学技术,2010,44(4):430-435.

XUE Ruojun, DENG Chengcheng, PENG Minjun. Numerical simulation of passive residual heat removal heat exchanger[J]. Atomic Energy Science and Technology, 2010, 44(4): 430-435(in Chinese).

[3]樊普，贾斗南，秋穗正. 低压下水欠热流动沸腾的两相CFD数值模拟研究[J]. 原子能科学技术,2011,45(4):412-420.

FAN Pu, JIA Dounan, QIU Suizheng. CFD investigation of subcooled flow boiling model under low pressure[J]. Atomic Energy Science and Technology, 2011, 45(4): 412-420(in Chinese).

[4]陈二锋，厉彦忠，王斯民. 竖直环管内低压水过冷沸腾数值模拟[J]. 西安交通大学学报,2008,42(7):855-859.

CHEN Erfeng, LI Yanzhong, WANG Simin. Numerical simulation of subcooled boiling water in vertical concentric annulus under low pressure[J]. Journal of Xi’an Jiaotong University, 2008, 42(7): 855-859(in Chinese).

[5]LEE T H, PARK G C, LEE D J. Local flow characteristics of subcooled boiling flow of water in a vertical concentric annulus[J]. International Journal of Multiphase Flow, 2002, 28: 1 351-1 368.

[6]SHIN B S, CHANG S H. CHF experiment and CFD analysis in a 2×3 rod bundle with mixing vane[J]. Nuclear Engineering and Design, 2009, 239: 899-912.

[7]ASDOZI A, KREPPER E, PRASSER H M. Experimental and numerical investigation of one and two phase natural convection in storage tanks[J]. Heat and Mass Transfer, 2000, 36: 497-504.