最大度为4的外平面图的无圈边色数*

王艺桥, 舒巧君

(1.北京中医药大学 管理学院,北京 100029;2.杭州电子科技大学 理学院,浙江 杭州 310018)

本文仅考虑有限简单图.给定一个图G,用V(G),E(G)和Δ(G)分别表示它的顶点集、边集和最大度.图G的正常k-边染色是指映射c：E(G)→{1,2,…,k},使得相邻的边染不同的颜色;若G有一个k-边染色,则称图G是k-边可染的;边色数χ′(G)是指使得图G是k-边可染的最小整数k;无圈k-边染色是指图G的一个正常的k-边染色,使得任一个圈上至少有3种不同的颜色;无圈边色数a′(G)是指使得图G是无圈k-边染色的最小整数k.

若无混淆,下文均将Δ(G)简记为Δ.根据Vizing定理[1],Δ≤χ′(G)≤Δ+1.显然,Δ≤χ′(G)≤a′(G).

猜想1对任意图G,a′(G)≤Δ+2.

猜想1至今尚未得到证实,但对一些特殊图已被证明猜想1成立.Alon等[6]证明了确定一个图G的无圈边色数是一个NP-问题.关于完全二部图、最大度为3的图及最大度为4的图的无圈边色数的研究可参见文献[7-9].对于平面图G,Basavaraju等[10]证明了a′(G)≤Δ+12;后来文献[11]将上界Δ+12降到Δ+7.

若图G存在一个平面嵌入,使得它的所有顶点在一个面的边界上出现,则称G为外平面图.令H2n表示在2n-圈x1x2…x2nx1上添加n-1条弦x2x2n,x3x2n-1,…,xnxn+2后所得的图,Q表示在7-圈y1y2…y7y1上加弦y2y7,y2y6,y3y5,y3y6后所得到的图,如图1所示.

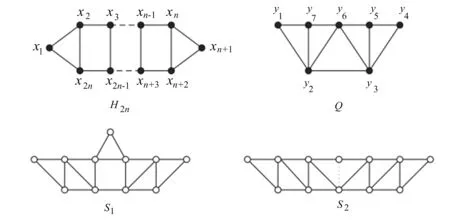
图1 图H2n,Q,S1和S2

设G是一个外平面图.2007年,Muthu等[12]证明了a′(G)≤Δ+1.文献[13]改进了这个结果,即证明了：当Δ≥5 时,a′(G)=Δ;当Δ=3且G是2-连通时,a′(G)=4当且仅当G含有与H2n同构的子图.此外,文献[13]还断言:若Δ=4,则4≤a′(G)≤5,且a′(G)=5当且仅当G含有与Q同构的子图.然而,这个结论是不正确的.事实上,王维凡等(在一篇未发表的论文中)构造出图S1和S2有a′(S1)=a′(S2)=5,但S1和S2均不含与Q同构的子图,如图1所示.

本文旨在给出一个最大度为4的外平面图的无圈边色数为4的一个充分条件.

在给出本文主要结论及其证明之前,先介绍外平面图的结构性质.

引理1[14]每个2-连通的外平面图G必含以下子结构之一(如图2所示):

1)2个相邻的2-点u和v;

2)一个3-圈uvwu使得d(u)=2,d(w)=3;

3)2个3-圈uvxu和u′v′xu′相交于一点x,使得d(u)=d(u′)=2,d(x)=4.

令M和(A1)～(A7)是如图3所示的子图形.

定理1设G是外平面图且Δ=4.若G不含子图与M同构,则a′(G)=4.

证明 假设G是一个最大度为4的外平面图,且不含与M同构的子图.只需证明G有一个无圈4-边染色c.若|V(G)|≤5,则结论显然成立.下设|V(G)|≥6.设G是边数最少的一个反例.将G嵌入在平面上.由文献[12],可设G是2-连通的.再由引理1知,G必含子结构(1)～(3)(如图2所示).用C={1,2,3,4}表示一个色集.

d(u)=d(v)=2 d(u)=2,d(w)=3 d(u)=d(u′)=2,d(x)=4(1) (2) (3) 图2 引理1中的子结构

1)G含有2个相邻的2-点u和v.

设u′≠v是u的另一个邻点,v′≠u是v的另一个邻点.令H=G-v+uv′,则H是一个外平面图且Δ(H)=Δ=4,|E(H)|<|E(G)|.若H不含子图与M同构,则a′(H)=4.由G的极小性知,H有一个无圈4-边染色c.此时,用c(uv′)染vv′,并用C{c(u′u),c(uv′)}中的某色染uv.否则,H中含子图与M同构.这也意味着G中含子图与(A1)同构.

令H′=G-uv,则H′是一个外平面图且Δ(H)=Δ=4,|E(H)|<|E(G)|.更进一步,H′中不含子图与M同构.由G的极小性知,H′有一个无圈4-边染色c.若c(uu′)≠c(vv′),则用C{c(uu′),c(vv′)}中的某色染uv.否则,c(uu′)=c(vv′).因d(v′)=3,故CC(v′)≠Ø.此时,用CC(v′)中的某色染uv.

2)G含有一个3-圈uvwu,使得d(u)=2,d(w)=3.

设x≠u,v是w的第3个邻点.

①假设d(v)=3或d(x)=2.

令H=G-uw,则H是一个外平面图且Δ(H)=Δ=4,|E(H)|<|E(G)|.更进一步,H不含子图与M同构.由G的极小性知,H有一个无圈4-边染色c.若c(uv)≠c(wx),则用C{c(uv),c(wx)}中的某色染uw.否则,c(uv)=c(wx).若d(v)=3,则用CC(v)中的某色染uw.下设d(x)=2.因|C(w)∪C(x)|≤3,故C(C(w)∪C(x))≠Ø.此时,用C(C(w)∪C(x))中的某色染uw.

②假设d(v)=4且d(x)≥3.

i)假设vx∉E(G).

令H=G-{u,w}+vx,则H是一个外平面图且dH(x)=d(x)≥3,dH(v)=3.若H不含子图与M同构,则a′(H)=4.由G的极小性知,H有一个无圈4-边染色c.不妨设C(v)={1,2,3},并有c(vx)=1.此时,用1染{uv,wx},4染vw,再用2染uw.易验证G没有双色圈.否则,H中含子图与M同构.这也意味着G中含子图与(A2)同构.令H′=G-{u,v,w,y},则H′是一个外平面图且Δ(H′)=Δ=4,|E(H′)|<|E(G)|.更进一步,H′不含子图与M同构.由G的极小性知,H′有一个无圈4-边染色c.不妨设C(x)={1,2,3}并有c(xy1)=2,c(xx1)=3.此时,先用4染{vu,xw},再分别用3,2,1染vy1,vy,vw.继而,若c(x1y1)=1,则用4染yy1,再用3染uw.否则,用1染yy1,再用2染uw.

ii)假设vx∈E(G).

设y≠u,w,x是v的第4个邻点.

假设xy∈E(G).因G是2-连通的且不含子图与M同构,故d(x)=4,d(y)=3.设x1≠y,v,w是x的第4个邻点,y1≠v,x是y的第3个邻点.令H=G-uw,则H是一个外平面图且Δ(H)=Δ=4,|E(H)|<|E(G)|.更进一步,H不含子图与M同构.由G的极小性知,H有一个无圈4-边染色c.若c(uv)≠c(wx),则用C(C(w)∪{c(uv)})中的某色染uw.否则,不妨设c(uv)=c(wx)=1.若对某个1∈CC(w),H中不含(1,a)(u,w)-路,则用a染uv.否则,下设对任意的i∈CC(w),H中含(1,i)(u,w)-路.因此,可再设c(xy)=c(vw)=2,c(xx1)=c(vy)=4,c(vx)=3及c(yy1)=1.此时,分别用1,3,2,4 染或改染{uw,vx},{wx,vy},uv及vw.可以发现G中没有双色圈.

假设xy∉E(G).令H=G-{u,v,w}+xy,则2≤dH(x)=d(x)-1≤3.若H不含子图与M同构,则a′(H)=4.由文献 [12]中的结论及G的极小性知,H有一个无圈4-边染色c.不妨设c(yx)=1,2∉C(x).此时,分别用1,2,3,4 染{vy,xw},{vx,uw},vw及uv.可以验证G中没有双色圈.否则,H中含子图与M同构.这也意味着G中含子图与(A3)～(A6)中的某个同构.

a)假设G中含子图与(A3)或(A4)同构.令H′=G-{u,v,w,x},则H′是一个外平面图且Δ(H′)=Δ=4,|E(H′)|<|E(G)|.更进一步,H′不含子图与M同构.由G的极小性知,H′有一个无圈4-边染色c.先设G中含子图与(A3)同构.不妨设c(yz)=1,c(yz1)=2及c(yy1)=3.此时,分别用1,2,4,3染{uw,vx},{uv,xz},{wx,vy}及wv.再设G中含子图与(A4)同构.不妨设c(yz)=1,c(zy1)=2及c(zz1)=3.此时,用1,4,2,3染{uw,vx},{uv,xz},{wx,vy}及wv.

b)假设G中含子图与(A5)同构.令H′=G-{u,v,w,y},则H′是一个外平面图且Δ(H′)=Δ=4,|E(H′)|<|E(G)|.更进一步,H′不含子图与M同构.由G的极小性知,H′有一个无圈4-边染色c.不妨设c(xy1)=1,c(y1z)=2及c(y1z1)=3.此时,先用2染{yv,xw}.继而,若c(xz)=3,则分别用4,1,3染{yy1,xv,uw},vw和uv.否则,c(xz)=4,分别用4,3,1染 {yy1,uv},{xv,uw}和vw.

c)假设G中含子图与(A6)同构.令H′=G-{u,v,w,x,z},则H′是一个外平面图且Δ(H′)=Δ=4,|E(H′)|<|E(G)|.更进一步,H′不含子图与M同构.由G的极小性知,H′有一个无圈4-边染色c.不妨设C(y)={1,2,3},c(yz1)=3及c(yy1)=2.先分别用1,2,3,4 染{xv,wu},xz1,xz和{xw,yv}.继而,若c(y1z1)=1,则分别用4,2,3染zz1,vw和uv.否则,c(y1z1)=4,分别用1,3,2染zz1,vw,uv.

3)G含有2个3-圈uvxu和u′v′xu′相交于一点x,使得d(u)=d(u′)=2,d(x)=4.

分2种子情形进行讨论:

①假设min{d(v),d(v′)}=3.

不妨设d(v)=3,并设y≠u,x是v的第3个邻点.令H=G-uv,则H是一个外平面图且Δ(H)=Δ=4,|E(H)|<|E(G)|.更进一步,H不含子图与M同构.由G的极小性知,H有一个无圈4-边染色c.若c(vy)≠c(ux),则用C{c(vy),c(ux)}中的某色染uv.否则,c(vy)=c(ux)=1.若c(u′v′)=1,则用c(xv′)染uv.否则,用c(xu′)染uv.

②假设d(v)=d(v′)=4.

假设vv′∈E(G).设z≠v,x,u′是v′的第4个邻点,y≠u,x,v′是v的第4个邻点.若y=z,则易证结论成立.因此,下设y≠z.此时,vz,yv′∉E(G).令H=G-{u,x,u′,v}+v′y.此时,dH(v′)=2.假设H不含子图与M同构.由G的极小性知,H有一个无圈4-边染色c.不妨设c(yv′)=1,c(v′z)=2.分别用1,4,3,2染{vy,u′v′,ux},{uv,xv′},{vv′,xu′}和xv.易见G中没有双色圈.

否则,下设H中含子图与M同构.这意味着G中含子图与(A7)同构.令H′=G-{u,x,u′,v,v′},则H′是一个外平面图且Δ(H′)=Δ=4,|E(H′)|<|E(G)|.更进一步,H′不含子图与M同构.由G的极小性知,H′有一个无圈4-边染色c.不妨设C(y)={1,2,3},并有c(yz)=1,yz1=2.此时,分别用4,1,2,3染{ux,u′v′,vy},{xu′,vv′},{v′z,xv}和{uv,xv′}.

假设vv′∉E(G).令H=G-{u,u′}+vv′.此时,dH(v′)=dH(v)=4,dH(x)=2,且H中不可能含子图与M同构(不然,会与外平面图的定义矛盾).由G的极小性知,H有一个无圈4-边染色c.不妨设c(vv′)=1,c(vx)=2及c(xv′)=3.分别用2,1,3,4染vx,{xv′,uv},{ux,u′v′}和xu′.

综上所述,均能得到G的一个无圈4-边染色,矛盾.定理1证毕.

由定理1立即得到下面推论:

推论1设G是Δ=4且不含相邻三角形的外平面图,则a′(G)=4.

参考文献：

[1]Vizing V G.On an estimate of the chromatic class of ap-graph[J].Diskret Analiz,1964(3):25-30.

[2]Alon N,McDiarmid C,Reed B.Acyclic coloring of graphs[J].Random Structures Alrorithms,1991,2(3):277-288.

[3]Esperet L,Parreau A.Acyclic edge-coloring using entropy compression[J].European J Combin,2013,34(6):1019-1027.

[5]Alon N,Sudakov B,Zaks A.Acyclic edge colorings of graphs[J].J Graph Theory,2001,37(3):157-167.

[6]Alon N,Zaks A.Algorithmic aspects of acyclic edge coloring[J].Algorithmica,2002,32(4):611-614.

[7]Basavaraju M,Chandran L S.A note on acyclic edge coloring of complete bipartite graphs[J].Discrete Math,2009,309(13):4646-4648.

[8]Basavaraju M,Chandran L S.Acyclic edge coloring of subcubic graphs[J].Discrete Math,2008,308(24):6650-6653.

[9]Basavaraju M,Chandran L S.Acyclic edge coloring of graphs with maximum degree 4[J].J Graph Theory,2009,61(3):192-209.

[10]Basavaraju M,Chandran L S,Cohen N,et al.Acyclic edge-coloring of planar graphs[J].SIAM J Discrete Math,2011,25(2):463-478.

[11]Wang Weifan,Shu Qiaojun,Wang Yiqiao.A new upper bound on the acyclic chromatic indices of planar graphs[J].European J Combin,2013,34(2):338-354.

[12]Muthu R,Narayanan N,Subramanian C R.Acyclic edge coloring of outerplanar graphs[C]//Kao Mingyang,Li Xiangyang.Lecture Notes in Computer Science 4508:Aspects in information and management.Berlin:Springer,2007:144-152.

[13]Hou Jianfeng,Wu Jianliang,Liu Guizhen,et al.Acyclic edge chromatic number of outerplanar graphs[J].J Graph Theory,2010,64(1):22-36.

[14]王维凡,张克民.Δ-匹配与边面全染色[J].应用数学学报,1999,22(2):236-242.