基于土石坝渗流和坝坡稳定的二维有限元分析

陈玉茹

(新疆维吾尔自治区塔里木河流域喀什管理局, 新疆 莎车 844700)

0 引 言

土石坝广泛应用于我国水利建设中，统计数据显示，截止到2010年，我国共有各类水库83 809座，其中石坝水库超过了83 000座.研究表明，30%的垮坝事故是由于土石坝渗流和坝坡失稳引起的[1].渗流是指水在岩土孔隙或裂缝中的流动现象，其流动性质与岩土性质和流体性质有关，目前认为土石坝的渗流规律满足达西定律[2].由于渗流骨架介质的孔隙大小形状不同，分布情况也十分复杂，因此很难求出水流质点的实际流速.渗流理论中一般利用平均参数和综合参数替代渗流性质.在恒定水头作用下，土石料渗透量随着时间的增加而减小；在变化水头作用下，土石料的渗透规律将不满足达西定律.

综合国内外土石坝数值模拟研究现状，基于二维拉格朗日有限差分法，建立了二维土石坝有限元分析模型.拉格朗日分析法求解中一般采用3种方法：离散模型法、有限差分法、动态松弛方法[3].采用ANSYS有限元软件，通过理论研究和数值模拟相结合的方法，对土石坝进行渗漏分析、渗透分析、坝坡稳定性分析，并给出了土石坝加固方案.

1 土石坝流固耦合模型的建立

达西定律是法国学者达西在1856年提出的，达西定律只适用于线性阻力关系的测流，对于惯性力和粘性力支配的渗流，并不能很好的进行求解，其认为渗流量[4]：

(1)

其中：k—土粒渗透常数；A—断面面积；

h—测压管的水头；L—渗流长度.

土粒渗透常数k表征了土粒的渗透强度，其与土石料材质、土颗粒级配、密实度、水的动力粘度、温度等因素有关[5].

渗流运动的液体受到质量力和表面力作用，因此可利用N-S方程、连续性方程、动量方程和能量方程对其进行分析.对于二维空间内的渗流，如果认为介质和水体是可压的，则推导出非稳定渗流微分方程为[6]：

(2)

其中：S—储水系数；kx、ky、kz—x、y、z方向的质量力.

通过ANSYS有限元软件建立数学模型，采用具有渗流特性的实体模拟流体流动.本文建立了土石坝流固耦合模型，流固耦合中孔隙水压力消失导致大坝土体发生沉降，其中主要包含两个力学变化：

(1)孔隙水压力变化导致大坝有效应力变化，可能导致塑性区的出现；

(2)孔隙水压力变化导致某一区域内的流体运动状态变化.

渗流数值计算分为各向同性、各向异性两种，分别采用相应的计算模型分析.非渗流材料采用null进行模拟，不同区域内可以采用不同的流动模型.流体源采用点源插入到材料中，对于饱和流动可以采用隐式算法.计算中主要根据达西定律的线性理论，假设材料参数恒定，并且不考虑对流.力学过程的特征时间为：

(3)

其中：Ku—不排水体积模量；G—剪切模量；

ρ—密度；Lc—模型的平均尺寸.

流固耦合计算中的储水系数为：

(4)

非饱和渗流的流体扩散率为：

(5)

其中：M—节点质量；α—扩散系数.

在渗流模型下，完全流固耦合模型分析需要从以下两方面进行[6]：

(1)孔隙压力改变影响体积应变和应力变化.

(2)体积应变变化会引起孔隙压力变化.

渗流力学扰动都是瞬间出现的，但是扰动导致的渗流作用时间往往相当长，例如土体中的孔隙水压力耗散和估计周期往往是几十小时.因此将扩散过程特征时间与流体力学特征时间的比值作为完全流固耦合模型分析的重点.

(6)

2 模型渗漏有限元分析

依据渗流理论，土石坝病害主要是由于渗流和渗漏引起的，因此有必要建立大坝有限元模.土石坝土体一般采用低渗透粘砂和碎石填筑而成，中间有一道砖结构的心墙，心墙的渗透系数远低于土石料，因此可近似认为心墙的渗透系数为0.将模型坝顶高度设置为1.2 m，坝基和坝体的参数(见表1).

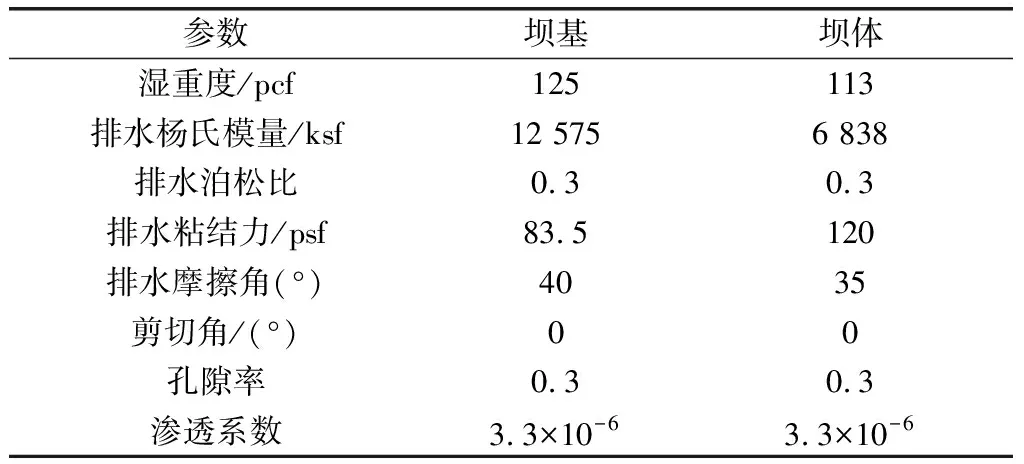
表1 模型坝基和坝体的参数

建立大坝的初始状态，假设初始时大坝土体中不存在超孔隙水压力.利用GAMBIT进行网格划分，模型为对称结构，砖砌心墙深入坝基，有限元模型网格划分(见图1).

首先计算初始压力下的孔隙水压和竖向应力情况，孔隙水压云图中可以清楚的看到心墙上的孔压情况，有些心墙单元处的孔压不为0，是因为ANSYS软件对节点信息进行了内插拟合.土石坝初始孔隙压力云图(见图2).

逐步上升水位，计算此情况在水压力的变化，导出的实验数据显示，初始孔压为1 000 Pa，水位上升后的孔压为10 kPa，模型内部的竖向应力为50 kPa，最大主应力为25 kPa.水位上升后的孔压云图(见图3).

由图3可以看出，孔压分布自上而下依次增加，同一深度下孔压云图分布较为均匀，从坝坡面开始到心墙处终止.利用软件模拟大坝内部的渗流路径，推断出坝体内浸润线的大体位置.水位上升后的渗流路径分布(见图4).

图1 有限元模型网格划分

图2 土石坝初始孔隙压力云图

图3 水位上升后的孔压云图

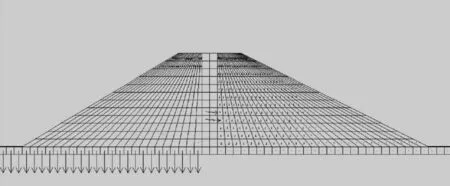
图4 水位上升后的渗流路径分布图

研究表明，设置的渗流通道不同，渗流量不同模拟出的渗流路径也不同.水位上升后，坝体内部孔隙压力、应力都明显增加，因此水位高度是坝体稳定性的重要影响因素.

3 渗流规律及加固措施

通过对土石坝流固耦合模型的数值研究，随着水位的不断增加，孔隙水压力增加，坝体内的渗流量扩大.因此，蓄水期引起的土石坝失稳因素主要有水压力、水位、水对上游石体的浮力等.蓄水前心墙处的孔隙水压力为0，蓄水后的孔隙水压力升高到10 kPa.说明水位升高后，坝体土石料的孔隙均被水填满，粗颗粒在地表水的作用下与坝基之间存在密切联系，图4中的水位渗流路径主要是垂向径流.

水位升高后，模型的渗流路径的位置相对提高.数值模拟得出的浸润线可以对土石坝防渗设计和加固改造提供参考.根据对土石坝渗漏规律研究，对于数值模拟的土石坝提出以下加固方案：

(1)鉴于坝体施工质量较差，确定加固范围为整个大坝上游砂壳.加固方法为采用复式压重体对上游坝基进行抛石压重处理.

(2)鉴于下游的坝坡缺土较为严重，坝面严重不平整，因此需对其进行补坡处理.

(3)由于当地经常发生地震，下游坝基石砂处存在液化区域，需要进行振动压实加固.

(4)为了防止渗流再次出现，采用方块石料作为上游护坡的加固材料.

(5)对心墙进行加高处理，分层填土并压实，使防浪墙与防渗体高度贴合.

(6)对于右坝肩渗水问题，对其进行静压灌浆加固，灌浆中心线布置在坝轴线上1.5 m处，利用水泥浆液进行灌浆.

4 结 语

渗漏通道高程直接影响渗流浸润线的水力坡降，高程越大坡降也就越大，渗透水头越大.采用二维拉格朗日有限差分法，建立了二维土石坝有限元分析模型.采用ANSYS有限元软件，通过理论研究和数值模拟相结合的方法，对土石坝进行渗漏分析、渗流规律分析、坝坡稳定性分析，并给出了土石坝加固方案.研究表明，渗流通道不同，渗流量不同模拟出的渗流路径也不同；水位上升后，坝体内部孔隙压力、应力都明显增加；孔压分布自上而下依次增加，同一深度下孔压分布较为均匀.希望为今后土石坝渗流研究提供帮助.

参考文献：

[1] 高江林.基于渗流与应力耦合的防渗墙与坝体相互作用研究[D].天津：天津大学,2012.

[2] 欧阳君,徐千军,侍克斌,等.土石坝边坡稳定性分析的温控参数折减有限元法[J].岩土力学,2011(8):2549-2554.

[3] 刘桃溪,辛全才,解晓峰,等.张沟均质土石坝渗流和坝坡稳定分析[J].人民黄河,2012(3):120-122.

[4] 段炎冲,安再展,李光耀,等.基于GeoStudio的某土石坝整治前后渗流及坝坡稳定分析[J].西北水电,2013(6):74-77.

[5] 马一霁,杨 媛.刚性防渗墙提高土石坝坝坡稳定性的作用机理分析[J].水利与建筑工程学报,2013(6):60-67.

[6] 李明超,苗 露,刘 菲.洪水作用下土石坝系统结构图仿真与渗流稳定性分析[J].应用力学学报,2014(1):110-115.