抽油机井杆管环空瞬态流场煤粉颗粒排出研究

刘 冰,杜继芸,綦耀光,张芬娜,莫日和,朱洪迎,黄芳宇

(1.中国石油大学机电工程学院,山东青岛266580；2.中联煤层气有限责任公司,北京100011)

抽油杆和柱塞的上下往复运动对抽油机井杆管环空流场产生扰动作用，属于复杂的周期性不稳定流动。一般把杆管环空中的周期性不稳定流动近似地按连续稳定流动来处理[1-5]，对固体颗粒的携带流速也是按平均流速近似计算[6-7]，与流体周期振荡流动的客观实际不符。目前针对具有运动边界的瞬态流场问题比较成熟的求解方法是动网格法。Margot等[8]对柴油机喷油嘴上下运动的流场进行基于动网格的仿真，获得多相流的质量流量随时间的变化。丁问司等[9]采用CFX自适应动网格技术对各典型振动条件下阀体及内外缸体内的交变流场进行数值模拟。熊万里等[10]提出基于纳维-斯托克斯方程的动网格计算轴承刚度阻尼的方法，有效避免因轴颈旋转引起的网格畸变，并利用弹簧光顺模型更新轴颈受速度扰动和位移扰动引起的油膜网格变形。笔者采用基于计算流体力学的动网格技术方法，对杆管环空内煤粉和水的瞬态两相流进行数值求解与分析，揭示杆管环空中煤粉颗粒在抽油杆扰动作用下的运动规律，并通过排煤粉的试验与数值模拟结果对比，验证基于动网格的数值计算方法的正确性。

1 数学模型

1.1 环空入口水流速度

杆管环空物理模型长度取为10 m即可满足流动的充分发展。初始时刻设定为抽油机悬点处于下死点位置的时刻，此时杆管环空内的流体处于静止状态，从初始时刻开始抽油机启动运行，驴头悬点在电机的带动下做上下周期往复运动，抽油杆可以近似地认为和悬点同步做正弦运动。抽油杆的速度为

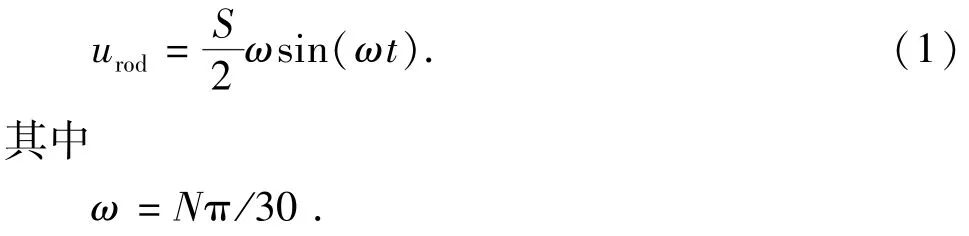
式中，S为冲程，m；ω为曲柄轴角速度，rad/s；t为时间，s；N为冲次，min-1。

上冲程(图1(a))时抽油杆带动抽油泵柱塞向上运动，抽油泵的游动阀关闭而固定阀打开处于吸

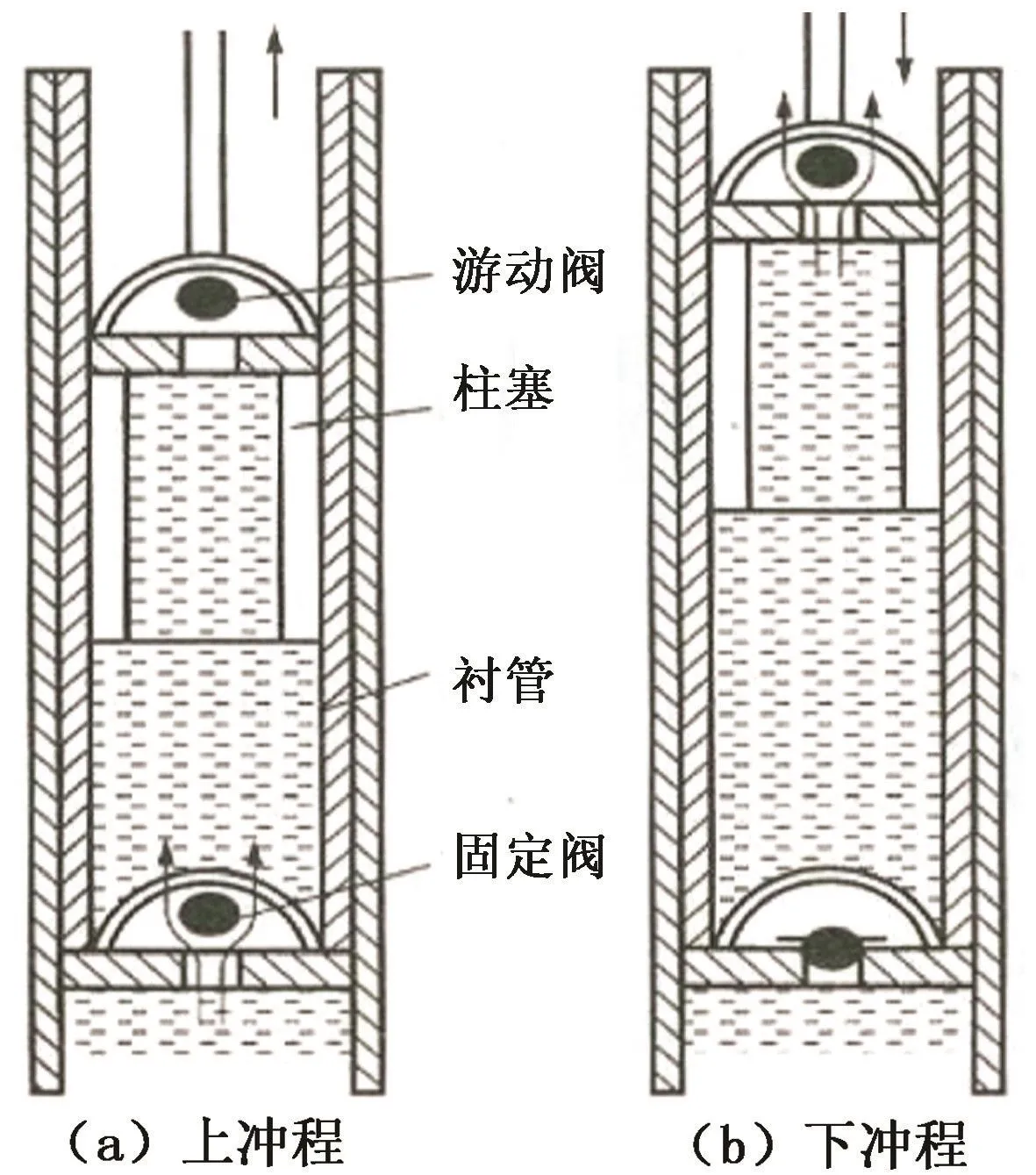
图1 有杆抽油泵的工作原理图Fig.1 Sucker rod pump work principle map

水状态，杆管环空内的水在抽油杆和柱塞作用下向上运动，环空入口水流速度为

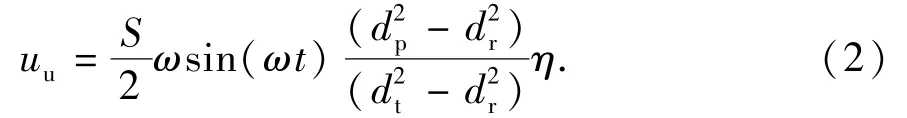
式中，dp为抽油泵柱塞直径，mm；dr为抽油杆直径，mm；dt为油管直径，mm；η为泵效，即抽油泵的实际排量与理论排量的比值。

下冲程(图1(b))时抽油杆带动柱塞向下运动，抽油泵的游动阀打开而固定阀关闭处于排水状态，杆管环空内的水仍然向上运动，环空入口水流速度为

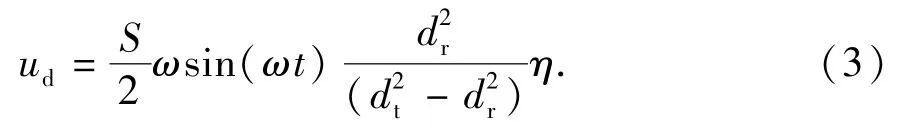
由式(3)可见，杆管环空入口水流速度为周期振荡流。抽油机工作时，杆管环空截面井液平均流速为

1.2 固液两相流模型

双流体模型是目前研究固体颗粒与流体的两相流最为广泛的一种方法，能够较完整地考虑颗粒相的输运过程，并通过颗粒压力和黏度考察颗粒间的相互作用。每相都应满足以下的连续方程[11]：

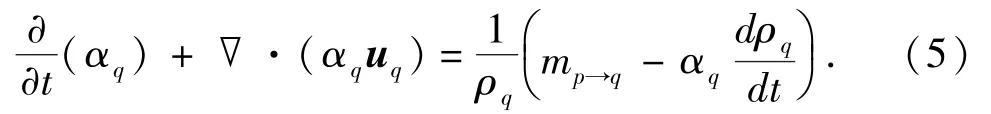
式中，αq为q相的体积分数；mp→q为从第p相到q相的质量传递；uq为q相的速度矢量；ρq为q相的物理密度；t为时间。

液相的动量方程为

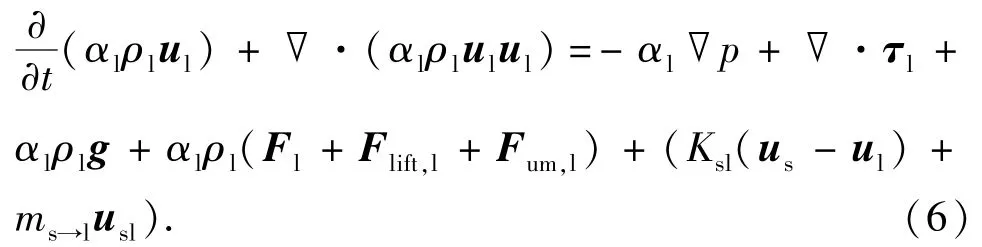
固相的动量方程为

式中，p为所有相共有的压力；τl、τs分别为液相和固相的压应力张量；Flift，l为固相流场的速度梯度引起的对液相的升力；Flift，s为液相流场的速度梯度引起的对固相的升力，特别是对于大粒径的煤粉颗粒，升力影响的作用较明显；Fum，l为液相相对于固相加速时产生的惯性质量力；Fum，s为煤粉颗粒的速度变化产生的虚拟作用力；Ksl=Kls为固液相间的动量交换系数，主要影响曳力函数。

1.3 动网格原理及求解方法

对于通量φ，在任意边界运动的控制体V，通用输运方程可表示为[12]

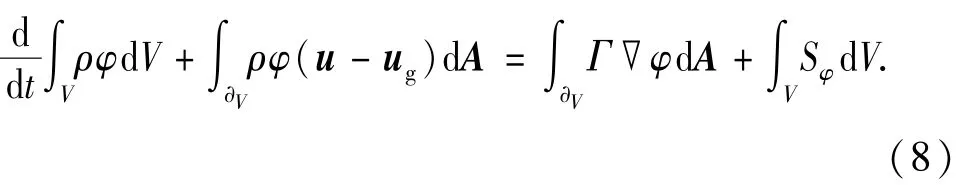
式中，ρ为流体密度；u为流体速度矢量；ug为动网格的网格变形速度；Γ为扩散系数；Sφ为通量的源项；∂V为控制体的边界。

采用一阶隐式格式，式(8)中的第一项可离散表示为

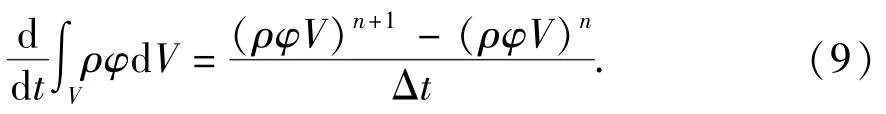
式中，n和n+1分别表示当前和下一时间步的数值。

第(n+1)步的体积Vn+1可表示为

表示控制体对时间的导数。为满足网格的守恒律[13]，控制体对时间的导数表达式为

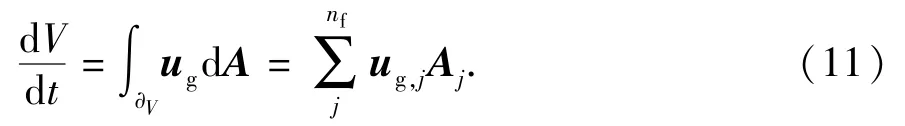
式中，nf为控制体中的面数；Aj为第j个面的面向量。

每个控制体的点积ug，j·Aj可表示为

式中，δVj为第j个控制体面在Δt时间内扫掠过的体积。

与结构化网格相比，非结构化网格更加适合处理具有大变形大位移的动边界问题，并且容易通过弹性变形或者重新生成网格的方法实现网格自适应的过程[14]，因此选择非结构化网格划分方法。

基于弹性变形的网格更新方法是将任意两节点之间的连线理想化成互相连接的弹簧[15]。运动边界节点上的位移将产生一个与所有连接到这个节点的弹簧位移对应的力，于是运动边界节点的位移以力的形式在流场中传播。根据Hook定律可得节点应力为

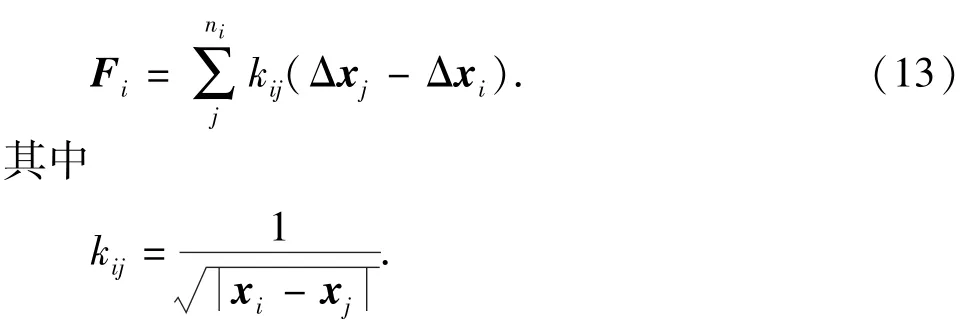
式中，Δxi和Δxj为节点i及其相邻节点j的位移；ni为与节点i相邻的节点数量；kij为节点和与之相邻节点之间的弹性常量系数；xi和xj为节点i及其相邻节点j的位置。

虽然弹性变形的网格更新方法中，网格拓扑结构始终不变无须插值，保证了计算精度，但当边界有较大位移或变形时，网格单元质量下降甚至出现不能继续求解的负网格。本文中抽油杆的运动位移远远大于网格单元的尺寸，必须在采用弹性变形的同时结合网格重新生成技术，在计算区域内插值重新生成网格，以适应计算区域的变化。单元将分裂成两个新的单元，网格被拉伸至满足

单元将与相邻的单元合并成一个新的单元，网格被压缩至满足

式中，hmin为单元最小高度；hideal为单元理想高度；αs和αc分别为单元分裂和合并因子。

图2为在不同时刻(T为抽油杆运动周期)的网格运动更新图。由图2可以发现，在抽油杆运动时，边界和求解区域内部的网格节点同时随边界运动，并且始终保持较高的网格质量，这是精确求解杆管环空非稳态流场的前提。

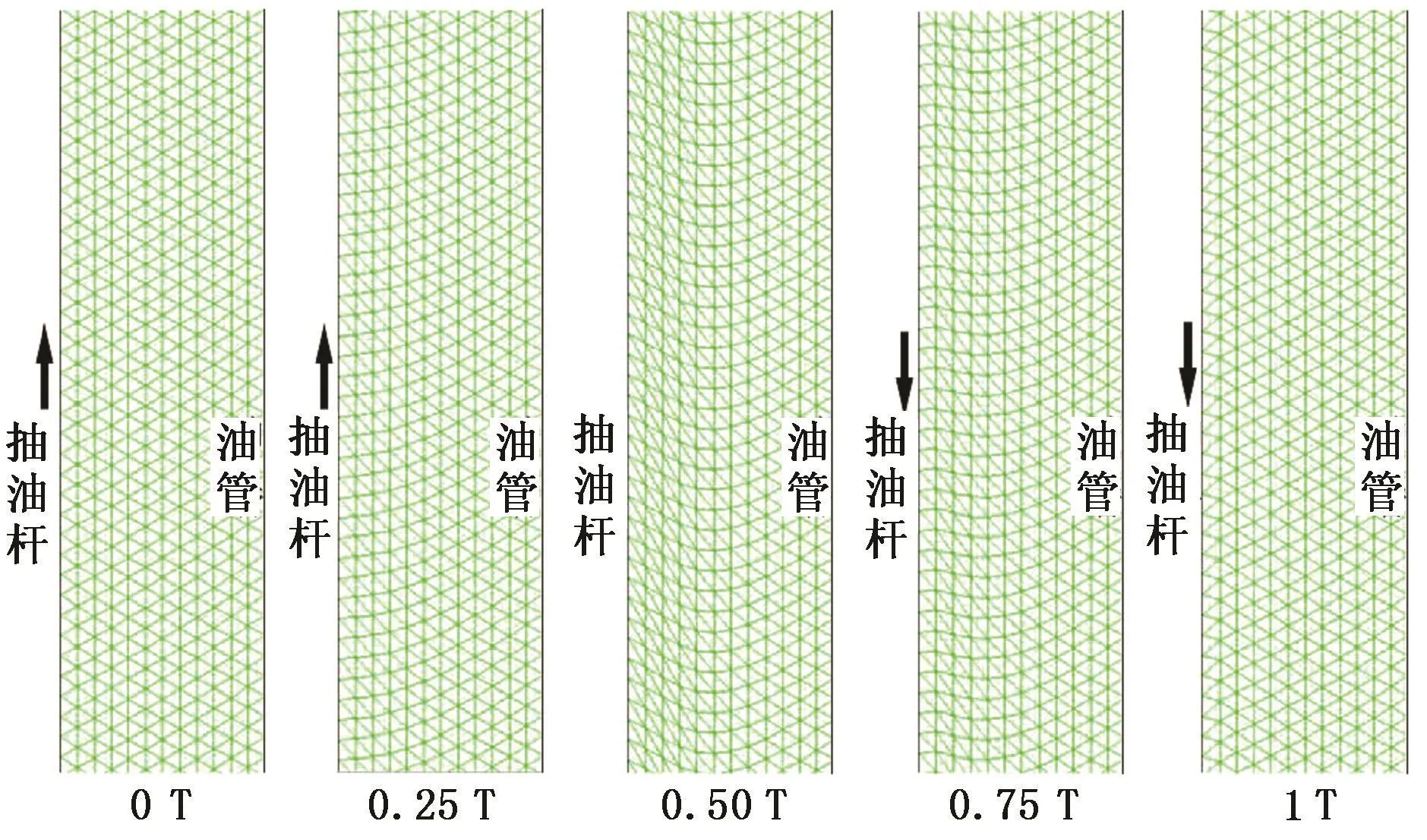
图2 网格运动更新图Fig.2 Grid movement update of dynamic mesh

1.4 煤粉排出量的计算

杆管环空入口和出口的煤粉颗粒的质量流量由当地截面的煤粉密度、速度以及网格单元面积点乘积分得

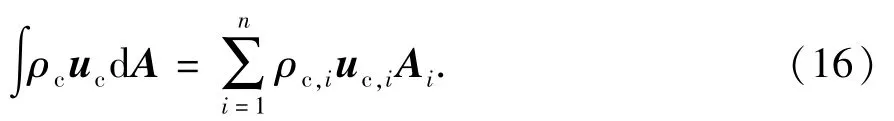
煤粉的质量流量对时间积分可以得到进出口煤粉的质量，进而求得煤粉的排出量。

2 数值计算及分析

根据对鄂尔多斯东缘区块多口煤层气井产出液的取样分析，煤粉的体积分数为2%～3%，因煤粉浓度越大越难以排出井筒，故设定煤粉在杆管环空入口处的体积分数为3%更具有代表性。煤粉颗粒的粒径范围分布为0.1～0.5 mm，其中粒径0.15～0.25 mm的煤粉占52.5%为最多，故设定粗、中、细3种典型煤粉颗粒的直径分别为0.5、0.2、0.1 mm，密度为1500 kg/m3。

入口边界采用速度入口条件，设定煤粉颗粒和水具有相同的初始速度。具体速度值由式(2)、(3)确定；出口边界采用自由出流的条件；在内壁面R=dr/2处，流体与抽油杆运动速度相等；在外壁面R=dt/2处，流体速度为零。壁面条件为反射。为了提高计算精度，对流项的离散采用二阶迎风差分格式，扩散项的离散采用具有二阶中心差分格式，速度与压力的耦合采用SIMPLEC算法，选择时间步长0.01 s，求解非稳态流场。

2.1 煤粉的速度分布

图3为以冲程1.5 m、冲次2 min-1工况为例的煤粉速度径向分布。径向位置由无因次半径R表示，抽油杆外壁处R=0，油管内壁处R=1。上冲程时抽油杆和杆管环空中的液体同时向上运动但速度大小不同，抽油杆的运动对煤粉速度径向分布产生较大影响：煤粉速度由抽油杆到油管呈递减规律分布，煤粉速度在抽油杆处有最大值0.035 m/s，在油管处有最小值-0.003 m/s。

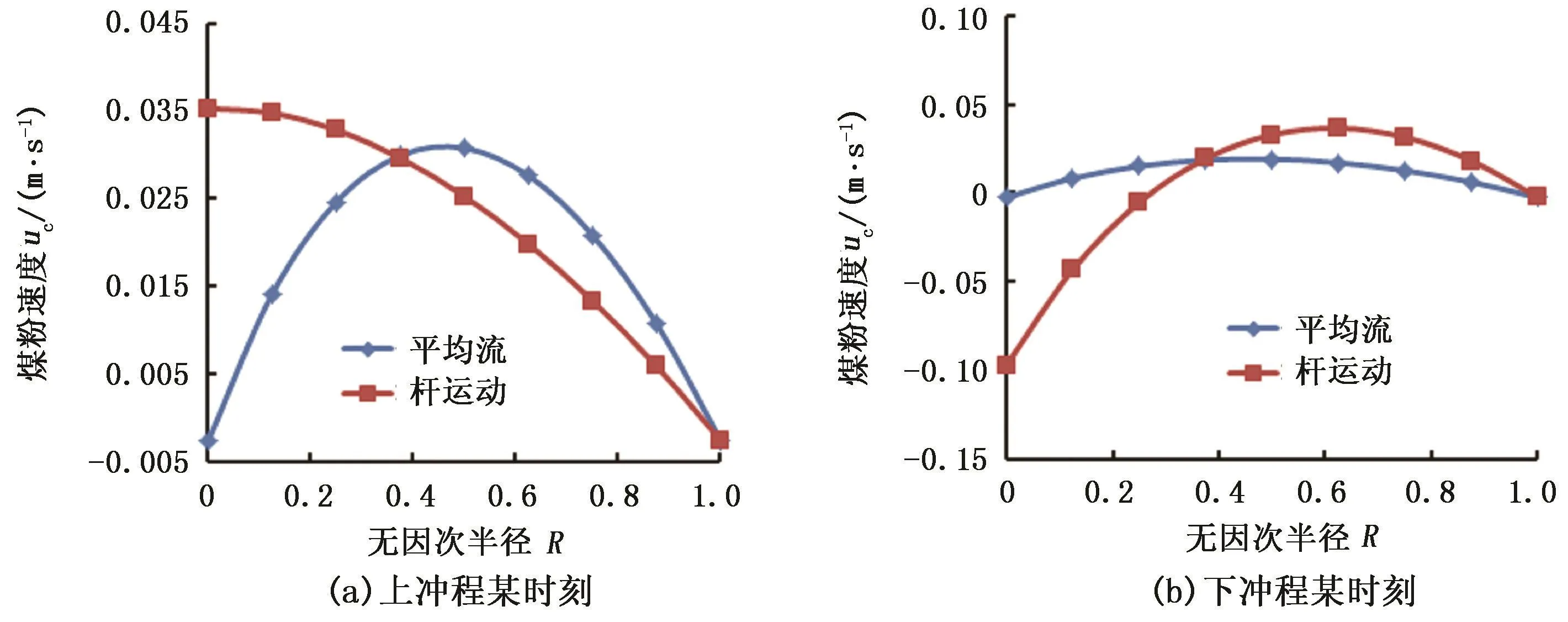
图3 煤粉速度径向分布Fig.3 Velocity radial distribution of coal particle

下冲程时由于抽油杆向下运动，杆管环空中的液体整体向上运动，抽油杆对流场的扰动作用增强，造成煤粉速度随着R增大呈现出先增大后减小的趋势。R=0处，煤粉速度最小值为-0.097 m/s；R=0.63处，煤粉速度最大值为0.036 m/s；R=1处，煤粉速度值为-0.003 m/s。

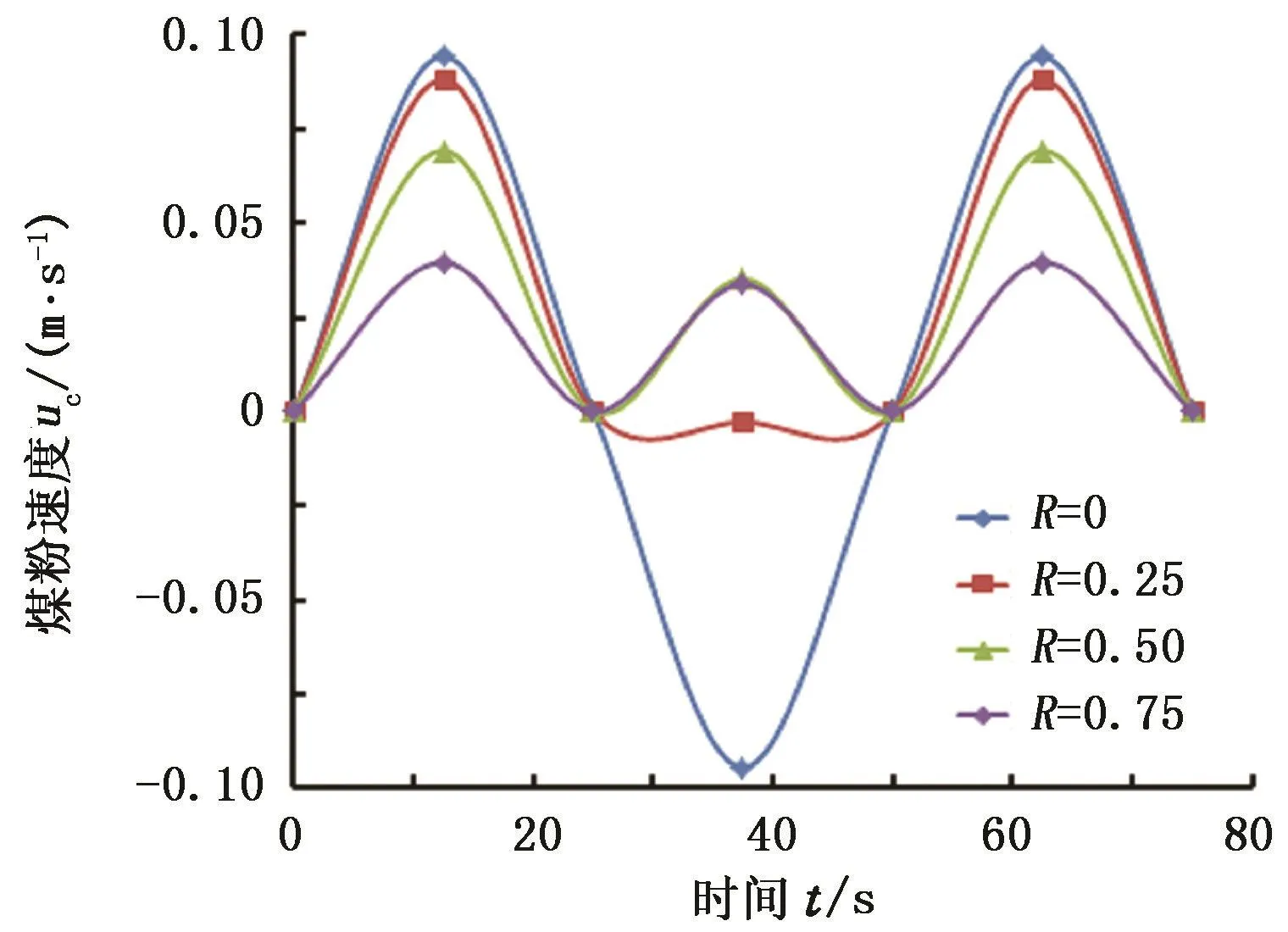
图4 煤粉速度时变Fig.4 Velocity time varying of coal particle

考察煤粉速度随时间的变化，在抽油杆的周期往复运动作用下，煤粉速度也呈现出周期性波动，图4给出了4个典型位置的煤粉速度曲线。由图4可以发现，随着径向位置增大，即越远离抽油杆，煤粉速度的波动程度越小。R=0处，煤粉速度波动程度最大；R=0.75处，煤粉速度波动程度最小，上、下冲程煤粉速度曲线几乎相同。

2.2 煤粉的浓度分布

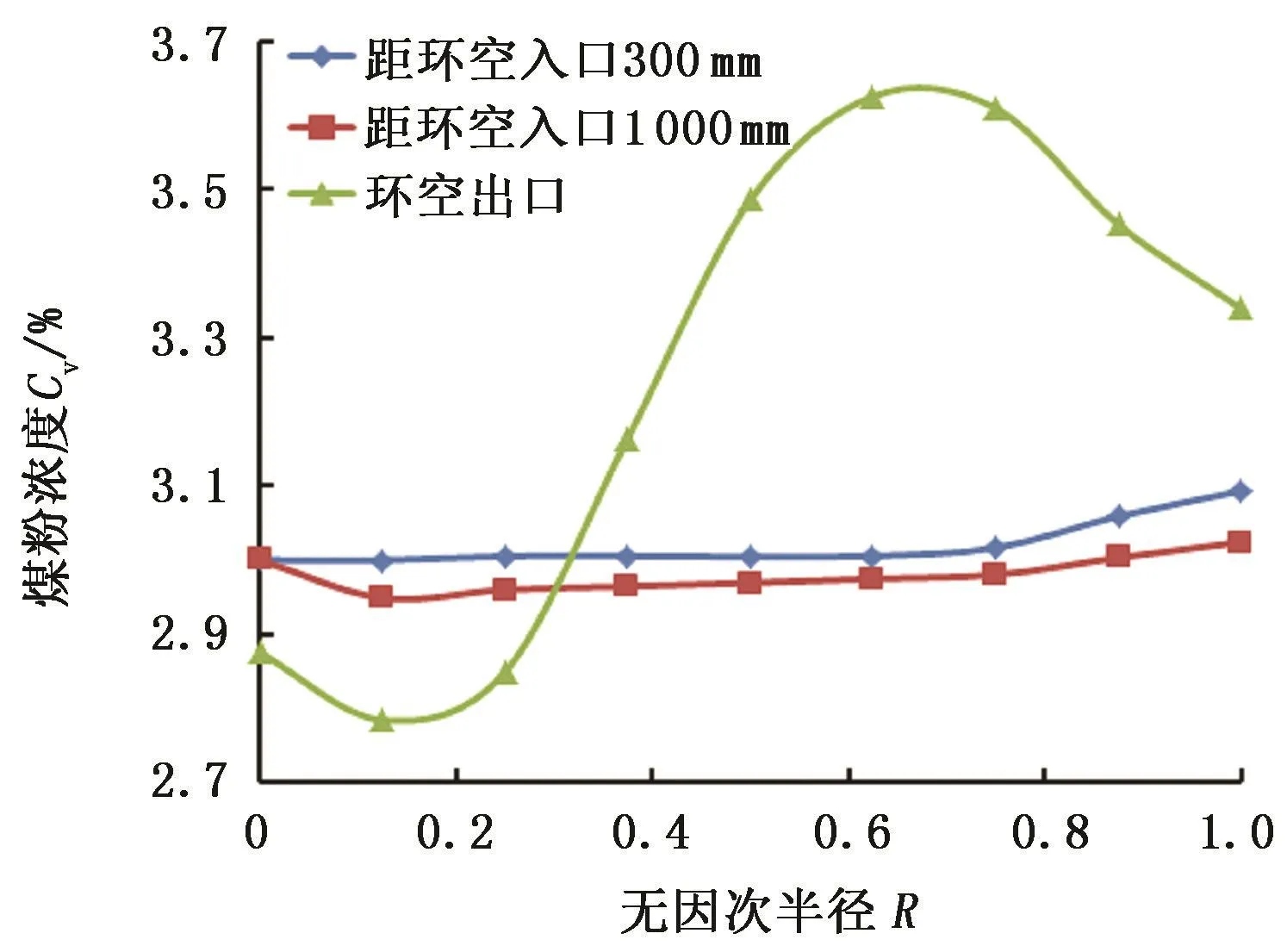
图5 煤粉浓度径向分布Fig.5 Concentration radial distribution of coal particle

伴随着固液两相流场的发展，在距离杆管环空入口不同距离处煤粉浓度分布不同。图5给出了距离杆管环空入口300、1 000 mm和杆管环空出口3个典型位置的煤粉浓度径向分布曲线。可以发现煤粉浓度从几乎均匀分布发展为波动分布；在杆管环空出口位置，经过流场的充分发展，煤粉浓度要高于入口附近的；在抽油杆附近煤粉浓度有最小值，在油管附近煤粉浓度有最大值。

可见，在包含抽油杆运动的杆管环空固液两相瞬态流场中煤粉的速度和浓度分布也是非稳态的。因此，须根据式(16)计算每个时间步长的煤粉质量流量，进而对时间积分得出杆管环空进出口煤粉的质量，最终求得煤粉的排出量。

3 试 验

3.1 试验装置

采用煤层气排水采气模拟试验装置(图6)。该装置杆柱和管柱的高度为30 m，包括螺旋锥齿轮调速减速机、抽油机、井口装置、储水装置、检测装置、套管柱、排采管柱、抽油杆柱和排采泵等，可以测量排液量、井底压力、产气量和煤粉量等。

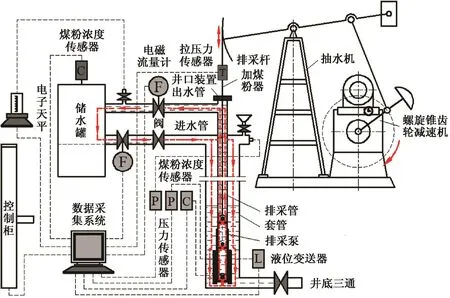
图6 排煤粉试验装置Fig.6 Coal particle clean out experimental facility

模拟试验装置的工作原理是：动力从地面经抽油杆柱传到井下，排采泵的柱塞在杆柱的带动下作往复运动，从而将井中的液体经由杆管环空输送至井口的三通，然后通过储水装置的出水管输送至储水罐中储存，并通过储水罐及时向井中补充井液，液体经由进水管输送至井口的四通，进入管套环空中，再经由尾管和泵柱塞进入杆管环空，由此实现模拟试验中井液的循环利用和井下动液面的相对稳定。另外，减速机将电动机、调速器和减速器集成在一起，保证试验中冲次在较大传动比范围内的连续调整；数据采集系统对试验中的数据进行实时采集、分析与处理。

3.2 试验方法

利用标准分级筛筛选出平均粒径分别为0.5、0.2、0.1 mm的3种煤粉颗粒。试验机型分别为冲程1.0和1.5 m，根据煤层气井进入稳产阶段日排水量在5～15 m3/d[16]，调节抽油机的冲次达到试验要求的排水量，具体参数见表1。按照煤粉在杆管环空中的体积分数，提前投入定量的煤粉颗粒，待煤粉全部沉降后开始煤粉颗粒排出试验。将井口排出液中的煤粉滤出烘干后使用电子称测量质量，计算在一定时间内煤粉的排出量。

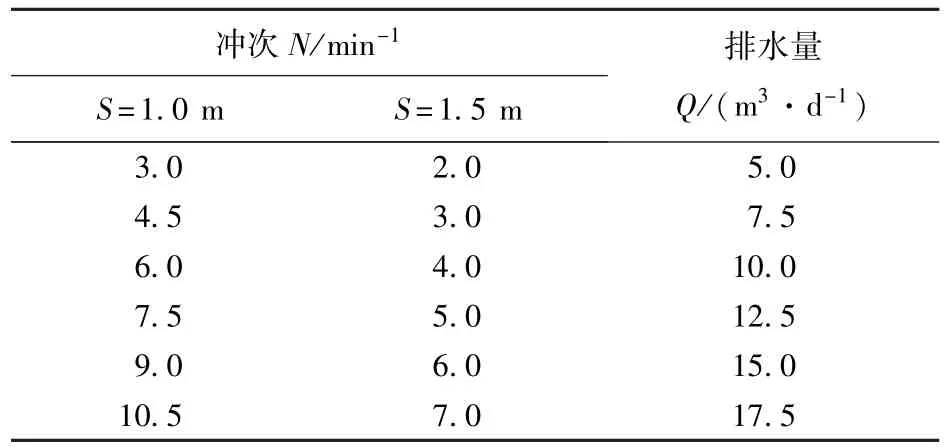
表1 排煤粉试验参数Table 1 Experimental parameters of coal particle clean out

3.3 试验结果及其分析

图7为不同粒径煤粉排出量的数值模拟与试验结果对比。由图7可知，数值模拟与试验结果基本吻合。数值计算值与试验结果存在一定差异的原因在于数值模拟中设置煤粉与壁面的碰撞条件是反射，而试验时观察到有小部分煤粉会黏在抽油杆和油管壁面上，而且煤粉粒径越小越容易吸附在壁面，因此随着煤粉粒径增大，试验值由低于模拟值变化到高于模拟值，且二者吻合度越来越高。冲程1 m比冲程3 m的模拟值精确度高，这是因为冲程越大动网格的畸变程度越大，网格的质量下降导致计算结果精确度的降低。

抽油杆的往复运动对杆管环空流场产生扰动作用，使得相同排量不同冲程冲次的抽油机井杆管环空的煤粉排出量不同，可以以此作为抽油机选型的方法。排量越小，煤粉粒径越大，煤粉排出量的差异就越大。例如排量5 m3/d、煤粉直径为0.5 mm时，工况为冲程1.0 m、冲次3 min-1比工况为冲程1.5 m、冲次2 min-1的煤粉排出量提高29%；而排量20 m3/d、煤粉直径为0.1 mm时，工况为冲程1.0 m、冲次12 min-1比工况为冲程1.5 m、冲次8 min-1的煤粉排出量仅提高1.5%，而且冲次太高会引起抽油杆偏磨加重的问题。因此，在低排量、大粒径、煤粉排出率不足90%的生产条件下，建议采用低冲程高冲次的机型提高煤粉的排出率，防止煤粉过度沉积在杆管环空底部导致卡泵；而在大排量、小粒径、煤粉排出率高于90%的情况，则不必提高抽油机冲次来降低冲程。

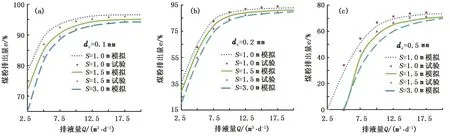
图7 煤粉排出量随排液量的变化Fig.7 Variation of coal particle clean out

4 结束语

用排煤粉试验证明了杆管环空瞬态流场数值求解结果的准确性，说明采用弹性变形和网格重新生成的动网格技术能够准确捕捉到边界和流场内部网格节点的运动，在边界做周期往复运动时保持较高的网格质量，是一种有效可靠的求解边界运动的非稳态流场的方法。抽油杆的往复运动对杆管环空流场产生扰动作用，使得排量相同即平均流速相同，不同冲程冲次组合的抽油机井杆管环空的煤粉排出量不同。这种差异在排量越小，煤粉粒径越大时越明显，可以此作为煤层气井抽油机选型的方法。若煤粉排出量低于90%，建议采用低冲程高冲次的机型提高煤粉的排出率，防止煤粉过度沉积在杆管环空底部导致卡泵；若煤粉排出量高于90%，则无须提高抽油机冲次降低冲程。

[1] IYOHO，ANIEKAN W，AZAR，et al.An accurate slotflow model for non-Newtonian fluid flow through eccentric annuli[J].SPE Journal，1981，21(5)：565-572.

[2] SHIGECHI T，LEE Y.An analysis on fully developed laminar fluid flow and heat transfer in concentric annuli with moving cores[J].International Journal of Heat and-Mass Transfer，1991，34(10)：2593-2601.

[3] XU Jun，SHIRAZI S A，DOTY D R，et al.Prediction of turbulent friction in rod pumped wells[J].SPE Journal，2000，5(2)：182-189.

[4] 郑俊德，刘合，阎熙照，等.聚合物产出液在抽油泵的缝隙中流动[J].石油学报，2000，21(1)：71-75.ZHEN Jun-de，LIU He，YAN Xi-zhao，et al.Flow of polymer output liquid in crevice of oil well pump[J].Acta Petrolei Sinica，2000，21(1)：71-75.

[5] YANG Shu-ren，WANG Chun-sheng，CUI Hai-qing，et al.Numerical simulation of steady flow for viscoelastic fluid in an eccentric annulus with inner rod moving axially[J].Journal of Hydrodynamics(Ser B)，2005，17(4)：514-518.

[6] 李明忠，王卫阳，何岩峰，等.垂直井筒携砂规律研究[J].石油大学学报：自然科学版，2000，24(2)：33-43.LI Ming-zhong，WANG Wei-yang，HE Yan-feng，et al.Experimental study on the performance of sand moving in vertical wellbore[J].Journal of the University of Petroleum，China(Edition of Natural Science)，2000，24(2)：33-43.

[7] 王治中，邓金根，孙福街，等.井筒砂粒运移规律室内模拟试验研究[J].石油学报，2006，27(4)：130-138.WANG Zhi-zhong，DENG Jin-gen，SUN Fu-jie，et al.Experimental study on sand grain migration in wellbore[J].Acta Petrolei Sinica，2006，27(4)：130-138.

[8] XANDRA M，SERGIO H，PABLO F，et al.A moving mesh generation strategy for solving an injector internal flow problem[J].Mathematical and Computer Modeling，2010(52)：1143-1150.

[9] 丁问司，巫辉燕.铁道车辆油压减振器三维流场动态仿真[J].机械工程学报，2011(6)：130-137.DING Wen-si，WU Hui-yan.Dynamic simulation of 3D flow field of train damper[J].Journal of Mechanical Engineering，2011(6)：130-137.

[10] 熊万里，侯志泉，吕浪，等.基于动网格模型的液体动静压轴承刚度阻尼计算方法[J].机械工程学报，2012，48(23)：118-126.XIONG Wan-li，HOU Zhi-quan，LÜ Lang，et al.M-ethod for calculating stiffness and damping coefficients ofhybrid bearings based on dynamic mesh model[J].Journal of Mechanical Engineering，2012，48(23)：118-126.

[11] VERSTEEG H K，MALALASEKERA W.An introduction to computational fluid dynamics：the finite volume method[M].New York：Wiley，1995.

[12] DEMIRDZIC I，PERIC M.Finite volume method for prediction of fluid flow in arbitrarily shaped domains with moving boundaries[J].International Journal for Numerical Methods in Fluids，1990，10(7)：771-790.

[13] DEMIRDZIC I，PERIC M.Space conservation law infinite volume calculations of fluid flow[J].International Journal for Numerical Methods in Fluids，1988，8(9)：1937-1050.

[14] HASSAN O.Mesh generation and adaptivity for the solution of compressible viscous high speed flow[J].International Journal for Numerical Methods in Engineering，1995，38(7)：1123-1148.

[15] BLOM F J.Consideration on the spring analogy[J].International Journal for Numerical Methods in Fluids，2000，32(6)：647-648.

[16] 刘新福，吴建军，綦耀光，等.煤层气井气体对有杆泵排采的影响[J].中国石油大学学报：自然科学版，2011，35(4)：144-149.LIU Xin-fu，WU Jian-jun，QI Yao-guang，et al.Effect of gas on sucker rod pump for coalbed methane well[J].Journal of China University of Petroleum(Edition of Natural Science)，2011，35(4)：144-149.