基于子孔径包络误差校正的SAR高精度运动补偿方法
田 雪 梁兴东 李焱磊 董勇伟(中国科学院电子学研究所 北京 100190)(中国科学院大学 北京 100049)
基于子孔径包络误差校正的SAR高精度运动补偿方法
田 雪*①②梁兴东①李焱磊①董勇伟①①(中国科学院电子学研究所 北京 100190)②(中国科学院大学 北京 100049)
目前,SAR正在向体积小、重量轻、功耗低的方向发展,由于受气流的影响,微小型SAR平台极易偏离理想航迹,大幅运动误差造成SAR图像质量严重下降,因此在微小型SAR成像处理过程中对运动误差的精确补偿十分重要。运动误差会造成包络误差和相位误差,传统运动补偿算法往往忽略包络误差的空变性,但是当运动误差幅度过大时空变的包络误差会对成像质量造成严重影响。该文提出与频分子孔径运动补偿算法相结合的包络误差校正方法,该方法消除了空变包络误差的影响,从而改善了成像质量。仿真和实测数据处理结果验证了该算法的有效性。
微小型合成孔径雷达;距离多普勒算法;两步运动补偿;子孔径方法;包络误差校正
1 引言
在合成孔径雷达(Synthetic Aperture Radar, SAR)成像的理论阶段,SAR聚焦是以SAR平台做匀速直线运动的理想假设情况为基础的,然而由于机载SAR在大气中飞行会受到气流等因素的影响而偏离理想航迹,带来运动误差,这些误差会引起雷达回波数据的幅度调制和相位调制,从而使SAR图像发生散焦、失真和几何扭曲等,因此运动补偿技术的研究对机载SAR成像处理有着重要的意义。
从20世纪70年代,国外就开展了运动补偿技术的相关研究。1973年,文献[1]研究了载机平台运动误差对SAR成像的影响,1975年,文献[2]给出了SAR运动补偿的基本概念与实现方法,定性分析了运动补偿的要求,揭示了运动补偿的必要性,接着文献[3-6]都对运动补偿问题进行了详细讨论和研究。国内多家科研院所及高校也在机载SAR运动补偿方面做出了卓有成效的研究工作并提出了一些有效的运动补偿方法[7-10]。
微小型SAR具有全天时、全天候、高分辨率、体积小、重量轻、功耗低、成本低、截获概率低等优点,可应用于平台成本低且不会带来人员伤亡的小型无人机(UAV)上,有着广阔的发展前景和应用前景。然而,由于微小型SAR平台轻小,气流不稳及平台性能等因素极易造成平台偏离理想航线[11],引起较大的运动误差,运动误差量往往在数十米量级,从而导致图像对比度下降,方位分辨率降低和图像几何失真,所以对运动误差的精确补偿成为成像算法中的关键技术。运动误差主要分为运动平台偏航引起的天线相位中心位置误差和平台姿态变化引起的角运动误差,运动补偿算法分为基于传感器测量数据的运动补偿算法和基于雷达回波数据的运动补偿算法两类[8],前者从载机平台上安装的运动传感器(如惯性导航系统、全球定位系统等)直接获取其测量的平台运动状态,后者从回波数据中提取运动误差,本文针对天线相位中心位置误差补偿问题,研究了基于传感器测量数据的运动补偿算法。传统运动补偿算法只对相位误差进行补偿,并没有对包络误差进行校正[9],但运动误差对信号产生的影响同样影响着距离压缩后峰值的位置,在运动误差较大的情况下,距离压缩后峰值位置不能很好地集中在一个距离门内,导致图像分辨率下降。随着机载SAR分辨率的提高,运动误差在距离向和方位向的空变性必须考虑。本文采用距离多普勒算法[12]对SAR数据进行成像处理,用两步运动补偿方法[13]对运动误差进行补偿,并在第2步运动补偿的时候提出用频分子孔径的方法对相位误差和包络误差均进行补偿,改善了运动误差较大时的图像质量,提高了图像分辨率,最后通过仿真处理结果和实测数据处理结果验证了算法的正确性和有效性。
2 SAR运动误差信号模型
设 SAR系统发射的线性调频信号中心频率为fc,调频率为Kr,信号包络函数为 wr(tr),则发射信号可表示为:
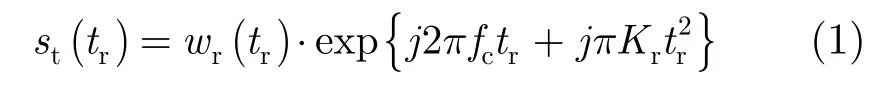
其接收信号为发射信号的延迟信号,设延迟时间为τ, τ=(2R)/c ,其中c为电磁波传播速度,R为雷达与目标的瞬时斜距,R=;瞬时斜距式中t为全时间,t=ta+tr, ta为慢时间,表示不同信号重复周期之间的时间变化,tr为快时间,表示每个信号重复周期内的时间变化;由于脉冲体制信号占空比小,脉冲宽度小,并且载机速度相对光速比较小,因此“走-停-走”模式有效,则R=; V为理想情况下平台匀速直线运动的速度;R0为目标最近斜距;wa(ta-ta,c)为方位包络函数,ta,c为波束中心偏离时间。则接收的回波信号为:
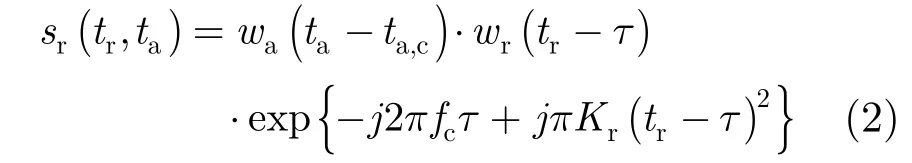
以上为平台做匀速直线运动的理想状态下的回波信号模型,当平台由于气流等因素偏离理想航线时,雷达与目标之间的距离会引入一个误差量ΔR,该误差量由传感器测量数据获取,加入运动误差的空间几何模型如图 1所示,图中x为距离向,y为载机飞行方向,即方位向,z为高度向,β为下视角。下文中假设点目标的散射系数为1。
则加入运动误差后的回波信号模型为:
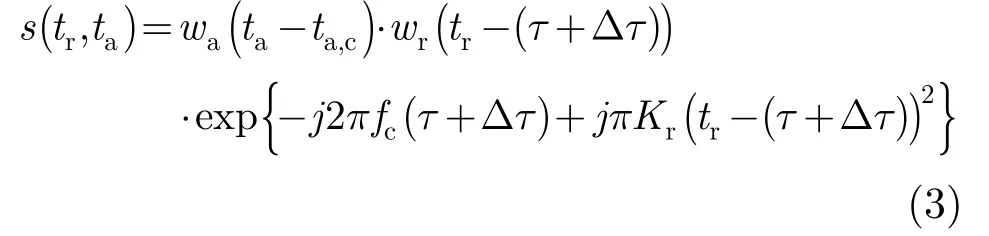
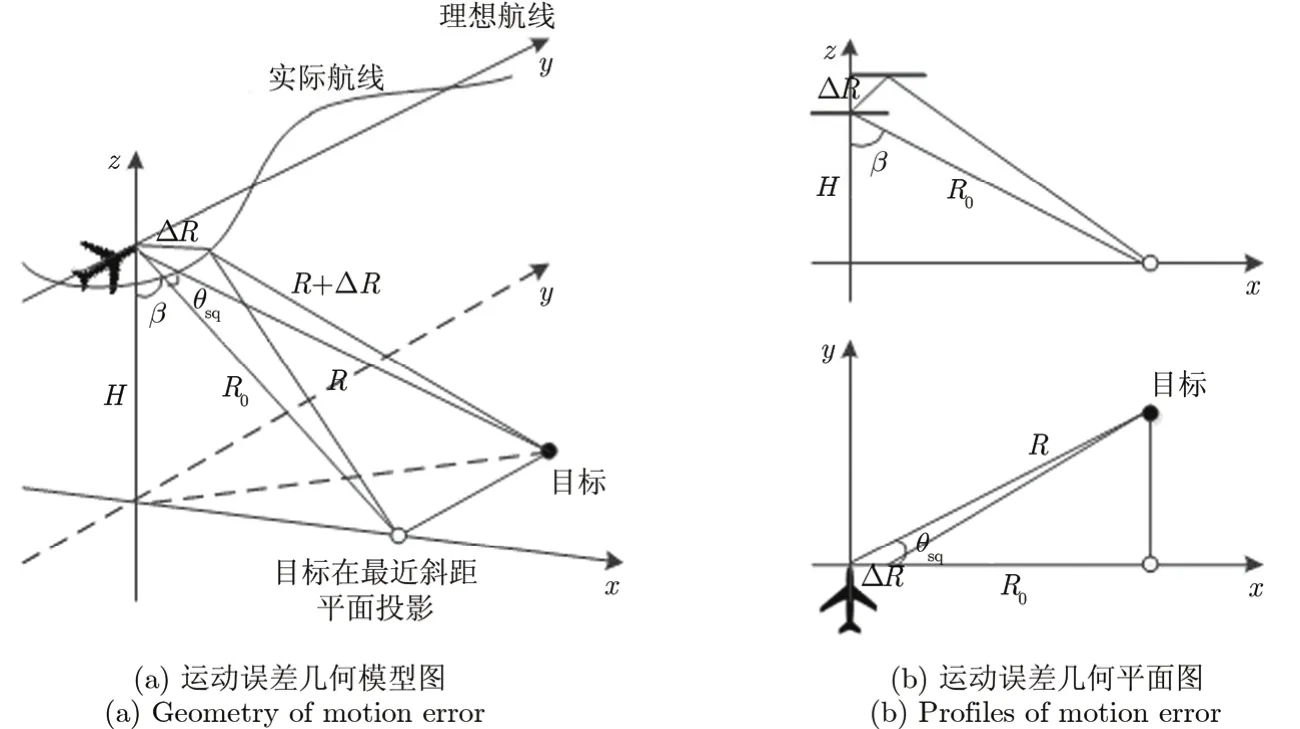
图1 平台运动非理想状态下的运动误差几何模型Fig. 1 Geometry of motion errorthat introduced by the imperfect platform movement
Δτ 为由运动误差量引起的回波延迟变化量,Δ τ=(2Δ R)/c。式(3)中第1项为方位多普勒信息,第2项为距离压缩需要的相位信息。从式(3)中可以看到,第2项距离压缩需要的相位项受到运动误差的影响,该影响在距离压缩时既影响距离压缩后信号的相位,同时也影响了信号压缩后的峰值位置,当峰值位置受其影响导致距离压缩后一个点目标的能量不能良好地聚在一个距离门内时,需要对信号做包络误差校正。由于微小型SAR平台轻小,极易受气流等因素的影响而偏离理想航线,运动误差量也会相对较大,所以包络误差校正的研究有其必要性。
3 传统运动补偿方法
3.1 一级运补
第1步运动补偿补偿与斜距无关的量,在距离压缩前取参考斜距在距离频域对所有信号进行相位补偿,一般将参考距离取为场景中心以使残余运动误差尽量小,设参考距离取为Rref,参考距离处的运动误差为δRref,由该运动误差引入的回波延迟变化量为δ τref, δτref=(2Δ Rref)/c 。将回波信号做距离向傅里叶变换得到回波信号在距离频域的表达式,可以得出一级运补的补偿因子为:
同时可进行距离向压缩,在距离频域乘上匹配滤波器 Hr(fr)=exp{ jπ(fr2/Kr)},再距离向逆傅里叶变换,即可实现距离向脉冲压缩。
3.2 二级运补
经过一级运补之后的信号除了在进行一级运补时选取的参考距离处补偿准确外,其它距离门内的目标均有残余误差,即该距离门处的实际运动误差与参考距离处的运动误差的差值,需要通过二级运补进行补偿。二级运补在距离压缩后进行补偿,对不同距离门补偿不同的运动误差量。
设距离压缩后,每个距离门处的运动误差为Δ Rr,根据几何关系推导可以得到其运动误差量的计算式为δ Rr=(- d x ⋅si nβr+dz ⋅cosβr)⋅cos θsq,其中, cosθsq为瞬时斜视角,dx, dz分别为运动误差Δ Rr的水平分量和竖直分量,如图2所示,βr为该距离门处的下视角。由该运动误差引起的延迟记为Δ τr,Δ τr=(2Δ Rr)/c 。
则二级运补的相位补偿因子可写为:

经过二级运补之后的方位残余空变量为Δ Rres=ΔR -ΔRr=(1-cosθsq)ΔR 。二级运补是在方位时域进行补偿的,忽略了信号的方位空变性,当方位空变较大,即 |(4 πδRres)/λ|max> π/N (N一般取4或8)时,需要对二级运补采用频分子孔径方法进行补偿。对不同的子孔径用不同的斜视角θsq,i计算运动误差量并用该运动误差量在方位时域进行补偿,再将补偿后的信号变到方位频域,截取出相应的子孔径范围,然后将不同的子孔径补偿后的信号在方位频域拼接起来。这样因对不同的子孔径采用了更精确的运动误差量进行补偿,从而减小了方位残余空变量,改善了方位向聚焦效果。
然而,距离压缩后的信号不仅相位受到运动误差的影响,距离向压缩位置也受到运动误差的影响,当运动误差较大使距离压缩后信号的能量在距离向不能聚在一个距离门内时,需要对信号做包络误差校正。在距离压缩之后,距离徙动校正之前进行二级运补的效果较之在距离徙动校正之后再进行二级运补的效果要好一些[14],故本文采用先做二级运补,再做距离徙动校正的方法。图3为根据传统方法,在做完运动补偿且距离徙动校正之后的峰值位置图,可以看到,经过距离徙动校正依然弯曲严重,残余运动误差已严重影响成像质量。
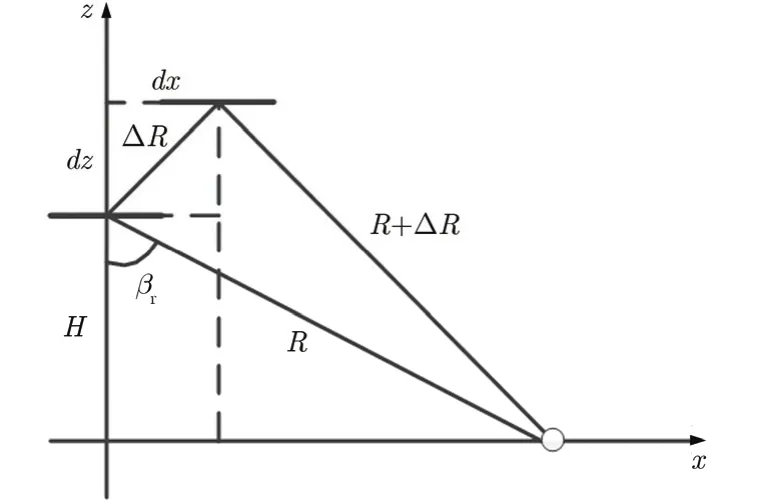
图2 运动误差量的计算示意图Fig. 2 Calculation of the motion error

图3 用传统运动补偿方法处理信号在距离徙动校正之后的峰值位置图Fig. 3 Peak position after RCMC with the traditional motion compensation method
4 基于包络误差校正的运动补偿方法
由第3节的分析可以看到,传统运动补偿方法在运动误差较大时已经不能满足高分辨率的要求,本节将从回波信号开始,具体分析基于包络误差校正的运动补偿方法。
将回波信号表达式(3)利用驻定相位原理(POSP)[15]沿距离向做傅里叶变换可以得到:

式(6)中第3项为距离向运动误差引起的回波包络延迟误差,第5项为方位向相位误差。对该信号进行一级运动补偿和距离向匹配滤波,可以得到:

将式(7)做距离向逆傅里叶变换回到2维时域,可以得到一级运补和距离压缩后的信号表达式:

由距离压缩后的信号表达式(8)可以看到,不仅相位受到运动误差的影响,距离向压缩位置也受到运动误差的影响。理想情况下,信号在距离向压缩后的峰值位置与目标和雷达之间的距离成正比,即峰值位置在=τ处,而受运动误差影响后,其峰值位置变为=τ+Δτ -Δτ 。用dt表示一个距refr离门的距离量,当> dtr时,在距离徙动校正之后一个点目标的能量不能很好地在距离向集中,会导致距离向压缩效果恶化,所以,在二级运补时也需要通过插值方法对包络误差进行校正,其校正量为:

包络误差校正可用线性相位相乘插值法,FFT补零插值法和截断sinc插值法[16],本文采用的是截断sinc插值法。在2维时域对每个距离门内的每个方位时刻按式(9)计算其包络需要校正的校正量,用sinc函数插值核 h(x)=sinc(x)=sin(πx)/(πx)对每个点在距离向进行插值,插值信号为g(x)=∑igd(i)s inc (x -i),其中 gd(i)为距离向采样后的信号。为精确计算g(x),需要对无限多个点求和,实际中往往在不过度损失精度的同时对插值核进行截断,通常取8点以下[16],本文算法中取8点插值。对插值核进行截断后,采样点上的权值和不再等于1,需要进行归一化处理。另外,当使用截断的sinc核对存在陡峭边缘的函数进行插值时会出现 Gibbs效应[15],本文采用对插值核进行kaiser锐化窗加权,以减小这种影响。
一般情况下,信号包络不如相位般对误差敏感,所以较少采用子孔径算法,因为包络补偿采用子孔径算法计算量会增大很多。但是同样,如果方位空变过于严重,导致目标距离向不能良好聚焦时,也需要采用频分子孔径的方法对包络误差进行校正,即在方位时域取不用斜视角计算补偿量对所有信号进行插值补偿,然后变换到方位频域,在方位频域取出该斜视角对应的多普勒频率附近的信号,再将不同斜视角情况下取出的不同频域信号拼接起来,以改善距离向压缩效果。由于在这一过程中分几个子孔径就要对所有信号做几次插值补偿,所以计算量增大很多,在处理中应根据实际情况适当选择子孔径数目。
经过二级运补后的信号变为:
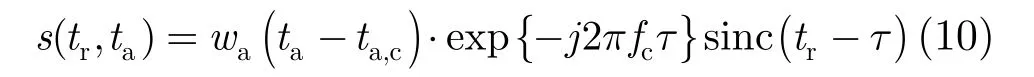
然后对信号进行 2次距离压缩和距离徙动校正,最后经过方位向匹配滤波即可得到聚焦效果良好的2维压缩信号。经过相位补偿和包络补偿,在运动误差较大的情况下也可以得到聚焦良好的图像。
5 仿真实验
为了验证上述分析的 SAR高精度运动补偿算法是否有效可行,本节进行了计算机仿真实验。首先根据建立的目标运动误差回波信号模型生成回波数据,设置如表1所示的仿真参数,水平向和垂直向均加入了峰峰值为10 m的运动误差,设平台匀速运动,姿态平稳,通过预先设定目标的位置,再利用本文讨论的运动补偿算法,观察在设定位置上是否有目标成像并量化分析成像质量指标来验证算法的有效性和可行性。本节的仿真参数选取依据本实验室研发的微小型SAR系统。

表1 仿真参数表Tab. 1 Parameters in the simulation
仿真成像处理结果如图4所示。图4(a)采用传统运动补偿算法,只做了相位的子孔径补偿,没有做包络补偿;图4(b)使用了子孔径方法对运动误差进行相位和包络的补偿,较之图 4(a)有了明显的改善;图 4(c)为没有做包络补偿的压缩结果(图 4(a))和做了包络补偿的压缩结果(图 4(b))的方位向和距离向点散布函数,图4(c)上图为距离向点散布函数,图4(c)下图为方位向点散布函数,蓝色线为图4(a)的点散布函数,红线为图4(b)的点散布函数,可以看到做包络补偿对压缩结果的改进,表2用具体质量指标量化地说明了包络补偿对图像的改善效果;图4(d)给出了距离徙动校正之后峰值位置的对比,蓝线为二级运补时不做包络补偿,距离徙动校正之后方位多普勒域的峰值压缩位置,红线为二级运补时做包络补偿,距离徙动校正之后方位多普勒域的峰值压缩位置,可以明显看到包络补偿使距离徙动校正之后的信号更直,信号能量在距离向更加集中,从而验证了本文算法的合理性和正确性。
6 实测数据处理
采用本文算法对本实验室研制的微小型 SAR系统的回波数据进行了运动补偿及成像处理,该系统工作在Ku波段,飞行高度约1200 m,速度约60 m/s,多普勒中心频率为500 Hz,波束宽度为10°,结果如图5所示。

图4 仿真结果图Fig. 4 Simulation results

表2 压缩结果质量指标对比表Tab. 2 Quality indicators comparison of compression results

图5 实测数据成像处理结果图Fig. 5 Imaging results of real data
从图5可以看到,通过本文的运动补偿和成像处理方法,得到了聚焦良好的图像,图5(c)和图5(d)为图像中相同区域的对比,图5(e)提取了图5(c)和图5(d)中所示的强散射点目标,并以点散布函数的形式在一个图中的对比,图中蓝线为传统算法的结果,红线为本文算法的结果,可以看到本文算法对成像的改善效果,更进一步验证了本文算法的正确性和有效性。
7 结束语
微小型 SAR因其具有独特的优势而备受各国研究者青睐,其较大的运动误差给成像处理带来了新的挑战。本文对方位空变较严重的运动误差采用频分子孔径的处理方法,不仅对相位误差进行补偿,并且对包络误差进行了有效的校正,减小了方位空变的影响,从而改善了压缩效果。从仿真实验和实测数据的处理情况可以看到该方法的有效性及合理性。
本文采用的是基于机载高精度运动传感器的运动补偿方法,相对运算量小,而对设备的要求高。但微小型SAR平台轻小,传感器的精度相对较低,这就需要结合另外一种基于雷达回波信号处理,从雷达回波数据提取运动误差并进行补偿的方法,这种方法对设备要求较低,而对算法要求较高,运算比较复杂,如自聚焦算法等,还有待进一步研究和优化。
[1] Farrell J L, Mims J H, and Sorrell A. Effects of navigation errors in maneuvering SAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, 9(5): 758-776.
[2] Kirk J C Jr.. Motion compensation for synthetic aperture radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1975, 11(3): 338-348.
[3] Buckreuss S. Motion errors in an airborne synthetic aperture radar system[J]. European Transactions on Telecommunications, 1991, 2(6): 655-664.
[4]Moreira A and Huang Yong-hong. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5): 1029-1040.
[5] Fornaro G and Sansosti E. Motion compensation in Scaled-FT SAR processing algorithms[C]. IEEE 1999 International Geoscience and Remote Sensing Symposium, Hamburg, 1999, 3: 1755-1757.
[6] Potsis A, Reigber A, Mittermayer J, et al.. Improving the focusing properties of SAR processors for wide-band and wide-beam low frequency imaging[C]. IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, NSW, 2001, 7: 3047-3049.
[7]周峰, 邢孟道, 保铮. 一种无人机机载SAR运动补偿的方法[J].电子学报, 2006, 34(6): 1002-1007.
Zhou Feng, Xing Meng-dao, and Bao Zheng. A method of motion compensation for unmanned aerial vehicles borne SAR[J]. Acta Electronica Sinica, 2006, 34(6): 1002-1007.
[8]保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 185-227.
Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 185-227.
[9]谭鸽伟. 合成孔径雷达的信号处理方法及运动补偿技术研究[D]. [博士论文], 中国科学院研究生院, 2008.
Tan Ge-wei. The study of signal processing and motion compensation for synthetic aperture radar[D]. [Ph.D. dissertation], Graduate University of Chinese Academy of Sciences, 2008.
[10]折小强, 仇晓兰, 韩冰, 等. 一种基于变换域的滑动聚束 SAR调频率估计方法[J]. 雷达学报, 2014, 3(4): 419-427.
She Xiao-qiang, Qiu Xiao-la, Han Bing, et al.. An improved Doppler rate estimation approach for sliding spotlight SAR data based on the transposition domain[J]. Journal of Radars, 2014, 3(4): 419-427.
[11]Fornaro G. Trajectory deviation in airborne SAR: analysis and compensation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 997-1009.
[12]Smith A M. A new approach to range-Doppler SAR processing[J]. International Journal of Remote Sensing, 1991, 12(2): 235-251.
[13]Zaugg E C and Long D G. Theory and application of motion compensation for LFM-CW SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 2990-2998.
[14]Li Yan-lei, Liang Xing-dong, Ding Chi-biao, et al.. A motion compensation approach integrated in the omega-K algorithm for airborne SAR[C]. 2012 IEEE International Conference on Imaging Systems and Techniques, Manchester, 2012: 245-248.
[15]Cumming I G, Wong F H著. 洪文, 胡东辉, 等译. 合成孔径雷达成像—算法与实现[M]. 北京: 电子工业出版社, 2007: 33-38, 47-49.
Cumming I G and Wong F H. Hong Wen, Hu Dong-hui, et al., translation. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Beijing: Publishing House of Electronics Industry, 2007: 33-38, 47-49.
[16]禹卫东, 吴淑梅. 距离-多普勒方法中的几种插值算法比较[J].电子与信息学报, 2001, 23(3): 308-312.
Yu Wei-dong and Wu Shu-mei. The comparison of some interpolation method for RD algorithm[J]. Journal of Electronics & Information Technology, 2001, 23(3): 308-312.

田 雪(1990-),女,籍贯河南,软件工程师,2014年7月获得中国科学院电子学研究所硕士学位,研究方向为调频连续波合成孔径雷达成像处理。
E-mail: tianxue326@gmail.com
梁兴东(1973-),男,籍贯陕西,研究员,研究领域包括高分辨率合成孔径雷达系统、成像处理及应用和实时数字信号处理。
E-mail: xdliang@mail.ie.ac.cn
李焱磊(1983-),男,籍贯河北,助理研究员,研究方向为机载差分干涉SAR信号处理。
E-mail: yllee@mail.ie.ac.cn
董勇伟(1982-),男,籍贯湖北,助理研究员,研究方向为雷达系统设计与实时信号处理。
E-mail: ywdong@mail.ie.ac.cn
High-precision Motion Compensation Method Based on the Subaperture Envelope Error Correction for SAR
Tian Xue①②Liang Xing-dong①Li Yan-lei①Dong Yong-wei①①(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)
②(University of Chinese Academy of Sciences, Beijing 100049, China)
Small size, light weight, and low power are presently the directions in SAR development. The microSAR platform is small and light, which results in track deviations because of air flow. The large motion error strongly affects the quality of SAR images. Therefore, high-precision motion compensation is important to SAR image processing. Motion error results in phase and envelope errors. Traditional motion compensation algorithms often ignore the space variance of the envelope error. When the motion error is large, the space-variant envelope error affects the image quality. This study proposes a high-precision motion compensation method based on the subaperture envelope error correction for SAR. The proposed method minimizes the effect of the space-variant envelope error and improves the image quality. Simulations and experimental data processing validate the correctness and effectiveness of the proposed algorithm.
MicroSAR; RD algorithm; Two-step motion compensation; Subaperture method; Envelope error correction
TN957.52
A
2095-283X(2014)05-0583-08
10.3724/SP.J.1300.2014.14068
2014-04-04收到,2014-04-30改回;2014-09-05网络优先出版国家部委基金资助课题
*通信作者: 田雪 tianxue326@gmail.com

