基于混合变分模型的图像去噪
周 杨,温兴平,张丽娟,王 军
昆明理工大学 国土资源工程学院,昆明 650093
基于混合变分模型的图像去噪
周 杨,温兴平,张丽娟,王 军
昆明理工大学 国土资源工程学院,昆明 650093
1 引言
图像在获取、传输、转换等过程中不可避免地会受到不同程度的噪声影响,导致图像分割、图像识别、图像分析、图像理解等处理结果出现较大误差,所以图像去噪成为图像处理研究领域中的热点问题[1]。
为了在去除噪声的同时较好地保持图像的清晰度、对比度、纹理信息等,大量的去噪方法相继出现[2]。传统图像去噪分为空间域处理和频率域处理:空间域去噪的主要思想是对噪声图像使用平滑滤波进行平滑处理,主要方法包含中值滤波、均值滤波和非局部平均滤波等[3-5]。频率域去噪主要通过Fourier变换、小波变换等将空间域信号转化为频率域信号,然后对频率域信号进行低通滤波,最后再转化为空间域信号[6-7],但基于空间域和频率域的图像去噪不能保持较好的几何机构。近年来,基于偏微分方程(Partial Differential Equation,PDE)的图像处理方法发展迅速,在图像去噪和去模糊等方面有着良好的应用效果[8]。其中基于全变分(Total Variation,TV),其是通过建立数学模型得到能量泛函,选取适当的参数,对图像进行反复迭代,通过解方程得到最优解从而得到很好的去噪效果。但其得到的图像无法较好地保持边缘,会产生“阶梯”效应。因此,为了改进算法缺陷,针对这两类经典模型存在的不足,人们提出了很多改进方法,文献[9]提出一种广义TV去噪模型,该模型能克服假边缘的产生,在去噪的同时保持了边缘细节,但该模型参数为常数,其取值对实验结果比较敏感。为克服该不足,文献[10]提出将梯度作为图像边缘的检测算子计算参数,文献[11]采用差曲率代替梯度作为边缘判别算子计算参数,文献[12]将非局部均值滤波引入参数中,这些改进方法都可根据图像的局部特征自适应选取参数的值,在不同程度上改善了图像去噪效果。然而,这些算法也存在缺陷,虽然能够很好地保持图像的边缘信息,但图像中细小的边缘会被过度平滑掉。
为了有效抑制噪声,获得更好的视觉效果,提出一种基于混合变分模型的图像去噪方法。首先将调和模型和全变分模型进行融合,增强模型的去噪性能,然后自适应选取加权参数,在有效减少噪声的同时,保护图像的边缘细节,最后采用多幅含噪图像进行仿真对比实验。结果表明,相对于其他去噪模型,相同条件下,本文模型不仅获得了较理想的视觉效果,提高了图像质量,而且获得了更高的峰值信噪比,有效降低了均方根误差,验证了算法的有效性。
2 混合变分模型
2.1 全变分模型
全变分模型去噪的基本思想是对含噪图像建立数学模型,得到相应的能量泛函,通过反复迭代使得能量泛函趋于极小值,这时可以认为噪声含量达到极小值,得到此时的解,即为去噪后的图像。设 f(x)∶Ω→R为图像空间Ω上的灰度图像,u(x)∶Ω→R为去除噪声后的图像,相似度函数定义如下:

基于上述定义,全变分模型的能量泛函定义为:

采用交替优化方法得到关于μ(x)的Euler-Lagrange方程和ωk+1的广义软阈值公式,μ(x)即为所得的去噪后图像。

2.2 调和模型
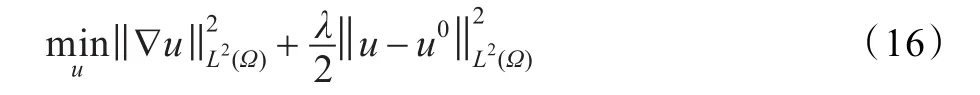
式中,∇u表示图像的梯度,ω为图像的定义域,λ为Lagrange乘子。
假定μ满足Neumann边界条件Ё∂u/∂ν=0,v表示∂Ω的外法向量,则调和模型存在唯一解且解满足最优性条件为:

2.3 混合变分模型
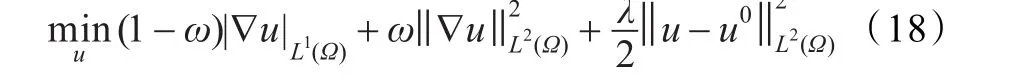
式中,ω为权函数,且0≤ω<1。
从式(18)可知,当ω=0时,相当全变分模型,其可以较好地保持边缘等细节信息;当ω=1时,相当于平滑较好的调和模型;当0<ω<1时,采用全变分模型处理图像的边缘细节,并采用调和模型处理平滑区域。
3 仿真实验
3.1 图像来源及仿真环境
为了验证本文模型的有效性,选择三种类型的图像作为仿真对象,具体如图1所示。仿真实验均在Intel®CoreTM2.85 GHz CPU,2 GB RAM,Windows 7操作系统,采用Matlab 2012编程实现仿真实验。

图1 含噪图像
3.2 结果与分析
分别采用调和模型、全变分模型和本文模型对图1中图像进行去噪处理,得到结果如图2~4所示。对图2~4进行分析可以得到如下结论:
(1)传统调和模型在去除图像中的噪声时,会去除图像的部分细节信息。
(2)相对于调和模型,全变分模型可以得到更优的去噪效果,但在平坦区域仍存在不同程度的“阶梯”效应。
(3)相对于对比模型,本文模型不仅减少了平滑区域的残余噪声,降低了边缘的模糊程度,同时可以较好保护图像的边缘细节,处理后图像整体质量较高,获得更加理想的视觉效果。

图2 lena图像的去噪结果
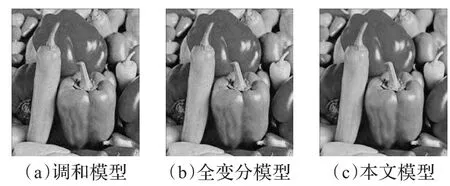
图3 Peppers图像的去噪结果

图4 Barbara图像的去噪结果
3.3 客观评价
在评价图像去噪模型性能时,有许多客观评价标准,本文采用峰值信噪比(PSNR)、均方根误差(MSE)和去噪时间作为模型去噪性能的客观评价指标[13],设M×N大小的带噪图像为 f(m,n),处理后的图像为 f′(m,n),其中m=1,2,…,M,n=1,2,…,N,则其计算方法如下:

其中,Q是量化级数。
调和模型、全变分模型和本文模型的PSNR和MSE如表1所示。从表1可知,本文模型具有较高的峰值信噪比,有效降低了均方根误差,因此在保护细节信息的同时。一定程度上缓解了图像的梯度效果,降噪性能比对比模型有了一定程度的改善。
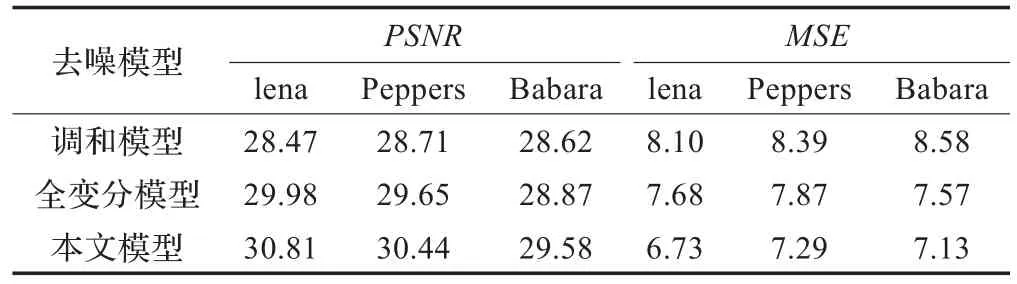
表1 各种模型的客观评价结果对比
调和模型、全变分模型和本文模型的去噪时间如图5所示,从图5可知,相对于全变分模型,调和模型的去噪时间相对较少,而本文模型的去噪时间要少于全变分模型,略高于调和模型,但是可以较高质量地恢复图像,因此综合性能最优。
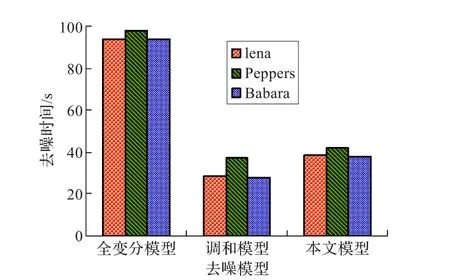
图5 不同模型的去噪速度对比
3.4 与经典去噪模型的性能对比
为了进一步测试本文模型的性能,采用当前经典图像去噪模型进行对比实验,它们分别为:Contourlet变换、小波阈值去噪、BM3D、BiShrink以及SURE-LET[13-16],所有模型的去噪效果评价指标如表2所示。从表2可知,相对于当前经典去噪模型,本文模型的PSNR值得到明显提高,MSE的值有所降低,对比结果再次证明了本文算法的有效性和优越性。

表2 与经典模型的性能对比
4 结束语
为了提高图像质量,有效去除噪声,针对全变分模型存在的不足,提出了基于混合变分的图像去噪模型,并通过仿真对模型的性能进行测试。仿真实验结果表明,本文模型具有良好的去噪性能,提高了图像质量,获得了更理想的视觉效果。
致谢 本文得到昆明理工大学地质过程与矿产资源省创新团队和昆明理工大学遥感地球化学学科方向团队联合资助,在此表示感谢。
[1]Al-amri S S,Kalyankar N V,Khamitkar S D A.Comparative study of removal noise from remote sensing image[J]. IJCSI International Journal of Computer Science Issues,2010,7(1):32-36.
[2]Mohammad R H,Ahmad M O,Wang Chunyan.An edgeadaptive laplacian kernel for nonlinear diffusion filters[J]. IEEE Transactions on Image Processing,2012,21(4):1561-1572.
[3]牛和明,杜茜,张建勋.一种自适应全变分图像去噪算法[J].模式识别与人工智能,2011,24(6):798-803.
[4]侯榆青,张欢,史晶,等.一种改进的全变分自适应图像去噪模型[J].西北大学学报,2008,38(3):371-373.
[5]Cho D,Bui T D.Multivariate statistical modeling for image denoising using wavelet transforms[J].IEEE Transactions on Signal Processing Image Communication,2005,20(1):77-89.
[6]戴维,于盛林,孙栓.基于Contourlet变换自适应阈值的图像去噪算法[J].电子学报,2007,35(10):1939-1943.
[7]刘文,吴传生,许田.自适应全变分图像去噪模型及其快速求解[J].计算机应用研究,2011,28(12):4797-4800.
[8]Beck A,Teboulle M.Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems[J].IEEE Transactions on Image Processing,2009,18(11):2419-2434.
[9]Yin Ming,Liu Wei,Shui Jun,et al.Quaternion wavelet analysis and application in image denoising[J].Mathematical Problems in Engineering,2012,2012:1-21.
[10]蔡良师,郑南山.基于小波系数相关性的图像去噪[J].测绘科学,2012,37(1):94-95.
[11]仵冀颖,阮秋琦.偏微分方程在图像去噪中的应用[J].计算机工程与应用,2006,42(22):69-71.
[12]高国荣,许录平,冯冬竹.利用非抽样Shearlet域GSM模型进行图像去噪[J].武汉大学学报,2013,38(7):778-782.
[13]贾建,焦李成,魏玲.基于概率模型的非下采样Contourlet变换图像去噪[J].西北大学学报:自然科学版,2009,39(1):3-18.
[14]郭强,郁松年.基于三变量模型的剪切波去噪方法[J].自动化学报,2010,36(8):1062-1072.
[15]Luisier F,Blu T,Unser M.A new SURE approach to image denoising:interscale orthonormal wavelet thresholding[J].IEEE Trans on Image Processing,2007,16(3):593-606.
[16]王凯,刘甲甲,袁建英,等.基于小波子带系数能量的优化权值降噪[J].计算机应用,2013,33(8):2341-2345.
ZHOU Yang,WEN Xingping,ZHANG Lijuan,WANG Jun
Engineering Institute of Land and Resources,Kunming University of Science and Technology,Kunming 650093,China
In order to restrain the noise and obtain better visual effect,a novel image denoising method is proposed based on hybrid variation model.The harmonic model and the total variation model are integrated to enhance the filtering performance,and then the parameters are adaptively selected.When combinatorial coefficient is large,hybrid model is close to total variation model,and when combinatorial coefficient is small,hybrid model is close to harmonic model to effectively remove the staircase effect to protect the edge detail.The simulation experiment is carried out to test performance of model. The results show that,compared with other denoising models,the proposed model has better denoising effect and can better protect edge information under the same conditions.
image denoising;harmonic model;total variational model;adaptive denoising
为了有效抑制噪声,获得更好的视觉效果,提出了一种基于混合变分模型的图像去噪方法。将调和模型和全变分模型进行融合,增强模型的去噪性能,根据自适应选取组合系数,组合系数较大时偏向于全变分模型,较小时偏向于调和模型,这样不仅可以有效去除阶梯效应,同时保护边缘细节,采用仿真对比实验以测试模型性能。结果表明,相对其他去噪模型,相同条件下,该模型取得更优的去噪声效果,提高了图像的质量。
图像去噪;调和模型;全变分模型;自适应去噪
A
TP317
10.3778/j.issn.1002-8331.1402-0417
ZHOU Yang,WEN Xingping,ZHANG Lijuan,et al.Image denoising based on hybrid variational filter model.Computer Engineering and Applications,2014,50(24):183-186.
国家自然科学基金(No.41101343);云南省高技术产业发展项目计划。
周杨(1989—),女,硕士生,主要从事遥感地质工作;温兴平(1970—),通讯作者,男,博士,教授,主要从事地球化学与遥感地质研究工作;张丽娟(1988—),女,硕士生,主要从事遥感地质工作;王军(1987—),男,硕士生,主要从事遥感地质工作。E-mail:wfxyp2008@gmail.com
2014-03-03
2014-05-13
1002-8331(2014)24-0183-04
CNKI网络优先出版:2014-07-16,http∶//www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0417.html

