一种基于误差修正的改进DV-Hop算法

王 林，赵 锦

西安理工大学 自动化学院，西安 710048

一种基于误差修正的改进DV-Hop算法

王 林，赵 锦

西安理工大学 自动化学院，西安 710048

1 引言

随着传感器技术、无线通信技术、微电子技术以及嵌入式计算技术等技术的发展，无线传感器网络得到了广泛应用。通过在目标区域部署大量传感器节点，可以实现军事防御、目标跟踪、环境监测、空间探索、医疗卫生监测等诸多应用。在众多应用中，没有位置信息的数据将毫无意义，位置信息的获取对于无线传感器网络的应用具有重要意义；同时位置信息也可辅助进行无线传感器网络的路由、拓扑管理等工作。因此，定位技术成为无线传感器网络的一项关键技术[1]。

目前，节点定位算法主要分为Range-based算法和Range-free算法两大类。其中Range-based算法主要包括信号到达时间（Time Of Arrival，TOA）、信号到达时间差（Time Differential Of Arrival，TDOA）、信号到达角度（Angle Of Arrival，AOA）、信号强度（Received Signal Strength Indicator，RSSI）等；Range-free算法主要包括质心算法、距离向量-跳段（Distance Vector-Hop，DV-Hop）算法、Amorphous算法、MDS-MAP算法及近似三角形内点测试法（Approximate Point-In-Triangulation test，APIT）算法等[2]。Range-based定位技术对网络节点的硬件要求较高；Range-free定位机制只需得到未知节点与相邻节点间的连通信息，然后利用各种优化方法估计未知节点位置，对硬件要求相对较低[3]。

DV-Hop算法是目前应用最广泛的无需测距定位技术之一，它具有算法简单和定位精度高等优点，适用于硬件支持有限的应用环境；但由于该算法的定位精度主要依赖于所估计平均每跳距离的精确度，对网络拓扑不规则的随机分布无线传感器网络来说，定位误差往往较大[4]。针对这个问题，许多学者对其进行了改进，文献[5-6]分别利用未知节点到参考节点的路径与参考节点间路径可能存在部分重合的特性修正平均每跳距离，在一定程度上提高了定位精度，但均未考虑网络拓扑的实际情况，因而不适合节点随机分布和网络拓扑动态变化的应用环境；文献[7]提出了一种基于接收信号强度指示和平均跳距修正的DV-Hop改进算法，但该算法需要进行高精度的强度测量；文献[8]在DV-Hop的基础上通过引入移动信标方式对算法进行改进，在一定程度上提高了算法的定位精度，但需要引入高精度的移动信标进行辅助定位。基于此，一些学者从不增加辅助硬件设备的角度对DV-Hop定位算法进行改进，文献[9-10]通过合理选择锚节点改善定位精度；文献[11]采用多个信标节点估计加权的方法对DV-Hop定位算法进行改进；文献[12]则通过Friis模型计算误差并采用误差加权的方法进行改进，均在一定程度上对传统DV-Hop定位算法有所改善。

然而，这些方法的研究均未考虑跳段的真实估计误差，本文在不引进辅助硬件设备的条件下，对DV-Hop算法进行分析，借鉴差分GPS（Global Position System）思想，利用信标节点的真实误差差分对未知节点距离估算进行补偿，设计一种基于误差修正的改进DV-Hop算法，以提高定位精度。

2 DV-Hop定位算法

DV-Hop算法由美国路特葛斯大学的Dragos Niculescu等学者提出[13]，其基本思想是将未知节点与信标节点之间的距离用网络平均每跳距离与节点之间最小跳数的乘积表示，并采用三边测量法获得节点位置信息。DV-Hop算法的实现大致分可为三个阶段：

第一阶段：计算每个未知节点与信标节点之间的最小跳数。信标节点向网络广播一个包含坐标(xi，yi)和跳数的信息包。邻近节点接收到信息包后，保存当前接收到的信息包并记录信标节点的位置坐标和跳数；接着将信息包更新，更新信息包只将跳数加1，而信标节点的坐标保持不变，然后继续向它的邻居广播更新后的数据包；如果某节点接收到来自同一个信标节点的多个信息包，则该节点只保留含有最小跳数值的信息包。

第二阶段：平均每跳距离计算以及距离估计。网络中每个信标节点在获得到其他信标节点位置和跳数信息后，计算网络平均每跳距离，然后将其作为校正值广播至网络中。信标节点平均每跳距离计算方法如下：

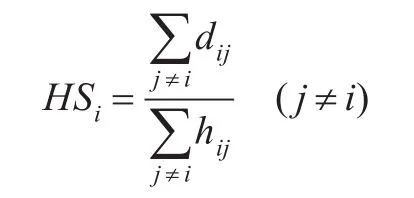
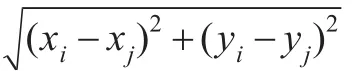
参考节点将计算得到的平均每跳距离广播至网络中，未知节点接收到平均每跳距离后，根据记录的跳数，计算到每个信标节点的跳段距离。则未知节点k到信标节点 j的估计距离为：

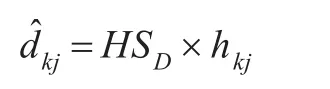
第三阶段：定位阶段。当获得到三个或更多个信标的距离信息时，利用三边测量法或极大似然法计算未知节点坐标。

算法定位过程如图1所示，已知信标节点L1与L2，L3之间的距离和跳数。L2计算得到的平均每跳距离为(40+75)/(2+5)=16.42，假设未知节点A从L2获得校正值，则它与各个信标节点之间的距离分别为L1∶3×16.42 =49.26，L2∶2×16.42=32.84，L3∶3×16.42=49.26，然后利用三边测量法确定未知节点A的位置。

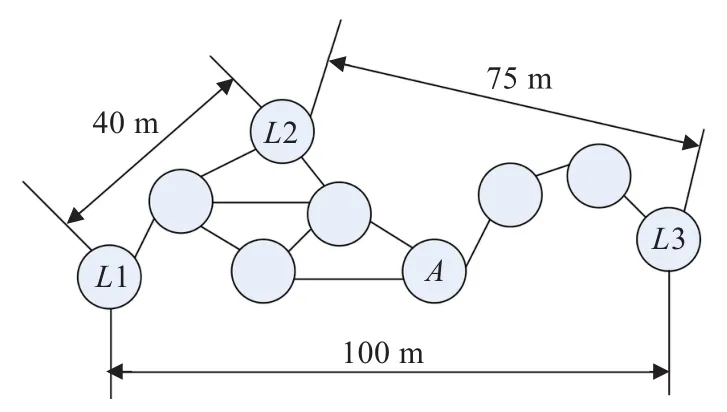
图1 DV-Hop定位算法示意图

3 DV-Hop定位算法改进

从上述DV-Hop定位算法原理可知，该算法需要经过跳数计算、距离估计和节点定位三个阶段。未知节点的定位精度与平均每跳距离的估计精度直接相关，一般来说，算法比较适用于各向同性的密集网络，对于随机分布的传感器网络，其定位误差比较大；然而在实际应用中，通常遇到的都是随机分布的传感器网络。为了改善DV-Hop算法针对随机分布传感器网络的定位性能，本文借鉴差分GPS思想，设计一种基于误差修正的DV-Hop改进算法，对DV-Hop算法中的每跳平均距离进行修正。

3.1 差分GPS基本原理

为了降低GPS信号传输过程中各种干扰、延迟、多路径效应等带来的定位误差，差分GPS在已知点（GPS基站）放置一台高性能的GPS接收机作为参考点。根据差分GPS基站发送的信息形式可将差分GPS定位分为伪距差分、相位平滑伪距差分、载波相位差分和位置差分。它们的工作原理均相同，都是由基准站发送改正数，用户站接收并以此为基础对其测量结果进行修正，以获得精确定位结果；不同之处在于发送改正数的内容不一样，修正方式不一样，所得差分定位精度也因此不一样。这里以伪距差分为例介绍差分定位原理[14]。

在伪距差分中，基准站（位置已知的站）的GPS接收并测量出全部卫星的伪距ρ以及星历文件，利用已采集到的卫星轨道信息计算各颗卫星的地心坐标 X，Y，Z。根据基准站的地心坐标 Xb，Yb，Zb，则可以求出每一时刻基准站到卫星的真实距离R如下：

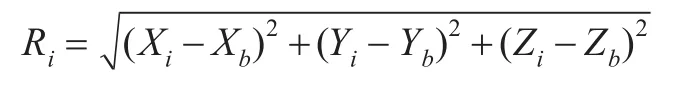
其中，i代表第i颗卫星。

因此，可以求出基准站GPS接收机测量中包含的各种误差，即伪距误差：

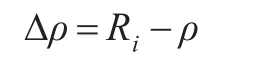
同时，也能求出伪距误差的变化率：

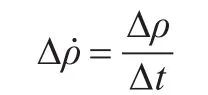
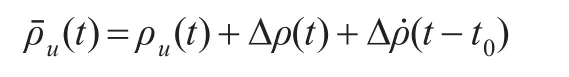
基于这一原理，本文将其应用于无线传感器网络中未知节点的定位问题，将信标节点作为参考节点，以此计算网络距离误差，并将其应用于未知节点与信标节点之间的距离估计。

3.2 DV-Hop定位算法改进

本文基于差分GPS原理，采用误差修正的方法对DV-Hop算法中平均每跳距离的估算进行修正，需要指出的是，改进方法并不改变DV-Hop算法的定位过程。主要改进包括修正误差计算和距离估计两部分，分别如下：

（1）修正误差计算

基于差分GPS原理，本文选取信标节点作为参考节点，在DV-Hop定位算法计算平均每跳距离的基础上，利用信标节点之间的实际距离与基于DV-Hop定位算法所得信标节点之间的估计距离之差作为修正误差。修正误差计算方法如下：

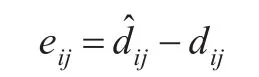
（2）距离估计

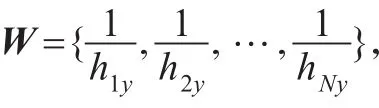
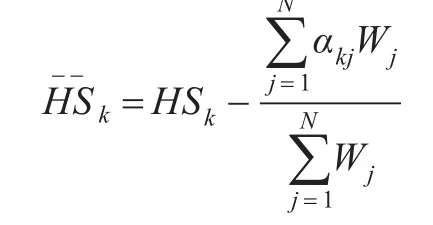
由此，可以得到信标节点z到未知节点 y的修正距离为：

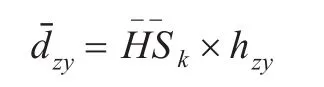
4 仿真

为了验证本文提出算法的有效性，利用MATLAB在假定场景中进行仿真。将总数为N的未知节点随机分布在20 m×20 m的正方形区域内，分别采用DV-Hop算法、文献[15]中的改进算法和本文设计的改进算法进行仿真对比研究。为便于分析对比，采用平均相对定位误差[16]衡量算法定位精度：

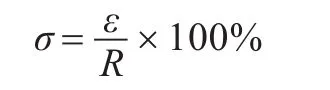
在实际仿真对比验证过程中，主要从信标节点数量对定位精度的影响、网络随机性对定位精度的影响以及计算复杂度三个方面对三种算法进行对比分析。

（1）信标节点数量对定位精度的影响

为分析信标节点数量对定位精度的影响，在仿真场景内随机部署50个未知节点，选择节点通信半径为6 m。同时，为使仿真结果更接近实际情况，所有仿真结果均通过20次独立仿真实验，各次仿真实验结果取平均获得。最终仿真结果如图2所示。

从图2可以看出：随着信标节点数量的增加，定位精度随之提高；信标节点越多，改进后算法比DV-Hop算法的误差减小更快。同时在相同数量信标节点下，改进算法定位精度均优于DV-Hop算法，平均定位误差相比原DV-Hop算法下降12%；从图中的对比也可以看出，改进后的定位算法相比文献[15]中的定位算法，在不同信标节点数量时定位精度均有一定提高。

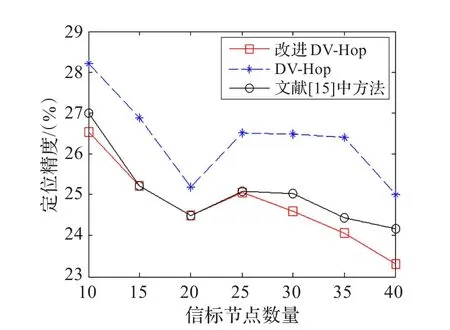
图2 定位精度随信标节点数量变化曲线

（2）网络随机性对定位精度的影响

为了分析未知节点随机部署对定位精度的影响，在设定场景中，选择未知节点数量为50个，并设置15个信标节点，选择节点通信半径为6 m，分别进行25次独立仿真实验，每次仿真均重新随机部署未知节点一次，信标节点的部署位置不变。所得仿真结果如图3所示。

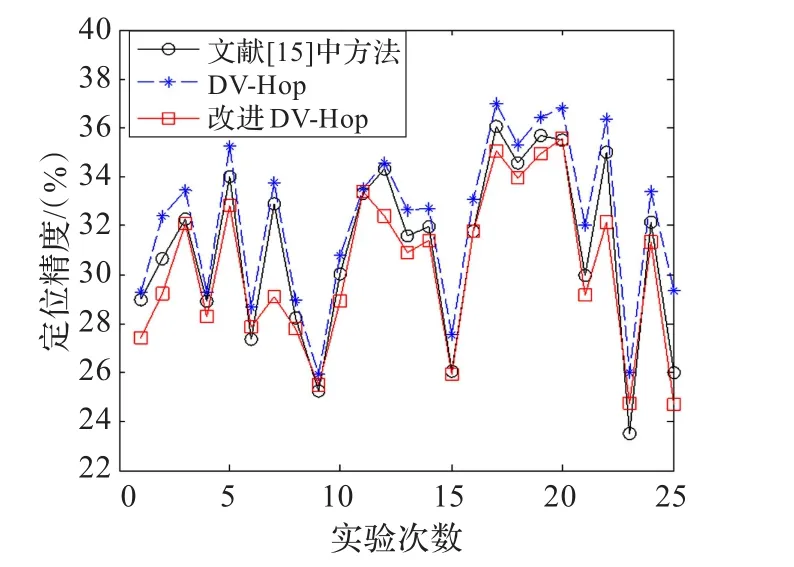
图3 不同实验定位精度

从图3的仿真结果可以看出：所进行25次实验中，每次实验改进算法定位误差均小于原DV-Hop算法；改进算法定位精度优于原DV-Hop算法以及文献[15]中的方法，其原因在于DV-Hop算法中采用跳段距离代替直线距离，存在较大的误差，而改进算法通过误差修正使得误差在一定程度上得到了补偿，定位精度也有了一定提高。

（3）算法复杂度分析

算法的计算量是算法应用中的一项重要指标。本文所设计算法由于其定位过程与DV-Hop一致，相比之下在误差修正中引入了额外的计算量。以N个信标节点为例，为了计算修正误差需要进行N×N次减法运算，N次除法运算得到加权因子W，对跳段修正需要进行减法运算与除法运算各N次，乘法运算N×N次，加法运算2N×(N-1)次。在文献[15]中，相比传统DV-Hop定位算法，计算平均跳距权值需要进行N×(N-1)次乘法以及除法运算，减法运算3N×(N-1)次；计算平均跳距需要进行N×N次乘法运算，2N×(N-1)次加法运算，N次减法以及除法运算；计算未知节点平均跳距同样需要进行N×N次乘法运算，2N×(N-1)次加法运算以及N次减法以及除法运算。计算量对比分析如表1所示。

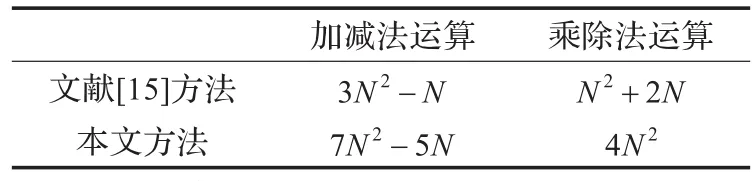
表1 计算量对比1）

从上述算法复杂度的分析可以看出，本文所设计改进算法相比传统DV-Hop定位算法计算量有一定提高，但相比文献[15]中的改进定位算法计算量明显降低。

5 结论

本文提出了一种基于误差修正的改进DV-Hop算法，在DV-Hop算法的距离估计阶段，基于差分GPS原理，对平均每跳距离进行误差修正，并进行了仿真研究。该算法基本保持了DV-Hop的定位过程，但不需要额外硬件支持。仿真结果表明，该改进算法定位精度优于原DV-Hop算法，同时受到网络随机性的影响较小。从与文献[15]的对比可以看出，本文定位算法的定位精度比文献[15]中方法有一定提高，但计算复杂度明显降低。尽管有一定改善，但如何进一步降低计算复杂度将仍是算法后续研究需要重点关注的一个方面。

[1]Liu Y，Yang Z，Wang X，et al.Location，localization，and localizability[J].Journal of Computer Science and Technology，2010，25（2）：274-297.

[2]赵欢，冯颖，罗娟，等.无线传感器网络的移动节点定位算法研究[J].湖南大学学报：自然科学版，2007，34（8）：74-77.

[3]彭宇，王丹.无线传感器网络定位技术综述[J].电子测量与仪器学报，2011，25（5）：389-399.

[4]李辉，熊盛武，刘毅.无线传感器网络DV-HOP定位算法的改进[J].传感技术学报，2011，24（12）：1782-1786.

[5]沈明玉，张寅.基于改进的平均跳距和估计距离的DV-Hop定位算法[J].计算机应用研究，2011，28（2）：648-650.

[6]Zhang Dengyi，Liu Feng，Wang Lei，et al.DV-Hop localization algorithms based on centroid in wireless sensor networks[C]//2012 2nd International Conference on Consumer Electronics，Communications and Networks（CECNET），2012：3216-3219.

[7]张爱清，叶新荣，胡海峰，等.基于RSSI每跳分级和跳距修正的DV-HOP改进算法[J].仪器仪表学报，2012，33（11）：2552-2559.

[8]谢晓松，程良伦.传感器网络基于移动信标改进的DV-Hop定位算法[J].计算机应用与软件，2011，28（4）：84-87.

[9]朱敏，刘昊霖，张志宏，等.一种基于DV-HOP改进的无线传感器网络定位算法[J].四川大学学报：工程科学版，2012，44（1）：93-98.

[10]肖丽萍，刘晓红.一种基于跳数修正的DV-Hop定位算法[J].传感技术学报，2012，25（12）：1726-1730.

[11]吴玉成，李江雯.基于最优节点通信半径的改进DV-Hop定位算法[J].华南理工大学学报：自然科学版，2012，40（6）：36-42.

[12]刘凯，余君君，谭立雄.跳数加权DV-Hop定位算法[J].传感技术学报，2012，25（12）：1539-1542.

[13]Niculescu D，Nath B.DV based positioning in ad hoc networks[J].Journal of Telecommunication Systems，2003， 22（14）：267-280.

[14]Yacob N，Abdullah M，Ismail M.Variation of elevation angle and Total Electron Content（TEC）and profile shape using modified jones 3D ray tracing for differential Global Positioning System（dGPS）in equatorial[C]//IEEE International Conference on RF and Microwave，2008：381-385.

[15]江禹生，冯砚毫.一种新的DV-Hop定位算法[J].传感技术学报，2010，23（12）：1815-1819.

[16]Yin Min，Shu Jian.The influence of Beacon on DV-hop in Wireless Sensor Networks[C]//Proceedings of the Fifth International Conference on Grid and Cooperative Computing Workshops，Hunan，2006：118-122.

WANG Lin,ZHAO Jin

The Automation Institute,Xi’an University of Technology,Xi’an 710048,China

Localization of nodes is one of the key technologies for the wireless sensor networks.An error compensation based improved algorithm is proposed to deal with the problem of DV-Hop algorithm in the localization of random distributed wireless sensor networks.Based on the principle of differential GPS,the proposed algorithm improves the distance estimation based on the error of beacons in the estimation stage of DV-Hop algorithm;and a multiple beacon errors weighted method is employed to revise the distance estimation.Simulation results prove the effectiveness of the proposed algorithm.

Wireless Sensor Networks（WSN）;Distance Vector（DV）-Hop algorithm;estimation of distance;error compensation;positioning accuracy

节点定位技术是无线传感器网络中的一项关键技术，针对DV-Hop算法对不规则随机分布网络定位误差较大的问题，提出了一种基于误差修正的改进算法。该算法借鉴差分GPS思想，在DV-Hop算法距离估计阶段，利用信标节点的误差差分修正估计距离；同时充分考虑网络实际，通过多信标误差加权的方式获得估计距离修正值，以提高算法定位精度。通过仿真研究验证了改进算法的有效性。

无线传感器网络；距离向量-跳段算法；估计距离；误差修正；定位精度

A

TP393.07

10.3778/j.issn.1002-8331.1302-0120

WANG Lin,ZHAO Jin.Improved DV-Hop algorithm based on error compensation.Computer Engineering and Applications,2014,50（24）：109-112.

航空科学基金项目（No.20110196005）。

王林（1963—），男，博士，教授，从事复杂系统与复杂网络、无线传感器网络信号处理技术研究；赵锦（1986—），通讯作者，女，硕士研究生，从事无线传感器网络信号处理技术研究。E-mail：593043944@qq.com

2013-02-22

2013-05-24

1002-8331（2014）24-0109-04

CNKI网络优先出版：2013-06-08，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130608.0953.002.html

◎数据库、数据挖掘、机器学习◎