具有变时滞阶段结构捕食系统的全局吸引性
伍代勇
安庆师范学院 数学与计算科学学院,安徽 安庆 246133
具有变时滞阶段结构捕食系统的全局吸引性
伍代勇
安庆师范学院 数学与计算科学学院,安徽 安庆 246133
1 引言
1990年,Aiello和Freedman在文献[1]中提出了如下具有阶段结构的单种群系统:
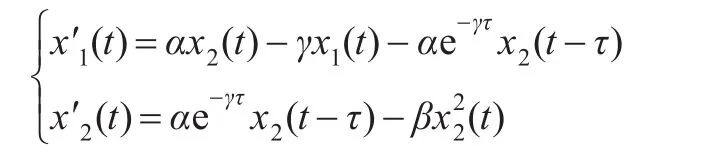
随后具有阶段结构捕食系统被广泛研究[2-9]。文献[3]研究了一类具有时滞和脉冲扰动下的相互干扰阶段结构捕食-被捕食系统。受文献[3]启发,本文将研究如下具有变时滞的相互干扰阶段结构捕食系统。
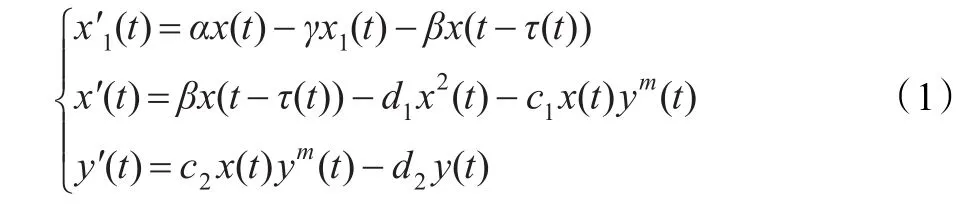
其中α,β,γ,di,ci>0,i=1,2,0<m<1,τ(t)为[0,+∞)上非负有界连续函数且τ1=inft≥0(τ(t))>0,记τ0=supt≥0(τ(t)),x1表示幼年食饵种群密度,x表示成年食饵种群密度,y表示捕食种群密度,α表示食饵种群的出生率,γ表示幼年食饵种群的死亡率,β表示食饵种群由幼年转化为成年的转化率,τ(t)表示食饵种群幼年的成熟周期,d1表示成年食饵种群的死亡和内部竞争率,m表示相互干扰常数,c1表示捕食种群捕获成年食饵的捕获率,c2/c1表示捕食种群捕获食饵后转化自身的转化率,d2表示捕食种群的死亡率。
考虑到种群的生态意义,假设系统式(1)满足如下初始条件:
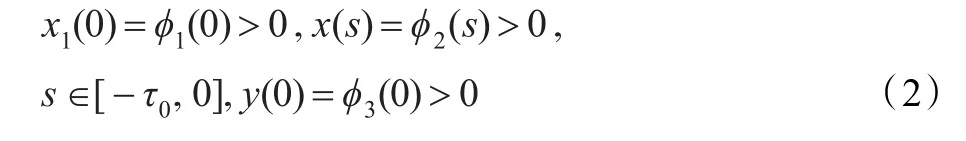
2 基本引理
引理1若 α>β,则系统式(1)有唯一正平衡态(x1*,x*,y*),其中x*为方程:
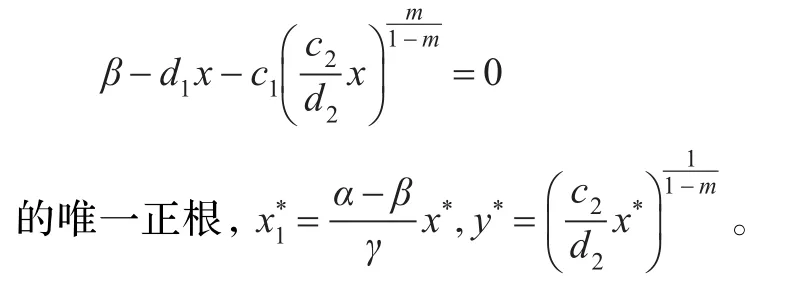
引理2对于任意的t≥0,系统式(1)满足初始条件式(2)的任意解为正的且最终有界。
证明 先证 x(t)>0(t≥0)。反证,若不然,则存在t′>0,使得 x(t′)=0。记t0=inf{t>0|x(t)=0},则t0>0。由系统式(1)的第二个方程得:
x′(t0)=βx(t0-τ(t0))>0
这与t0的定义矛盾。所以对∀t>0,有 x(t)>0。考虑方程:
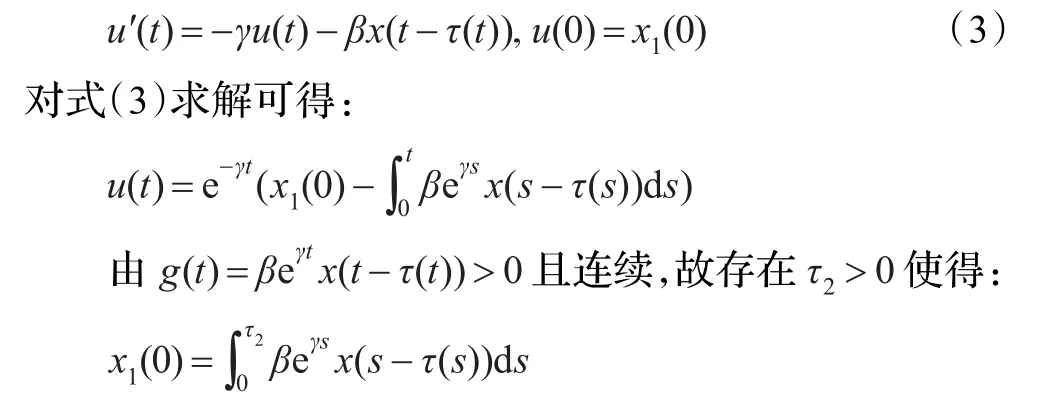
所以u(τ2)=0。因此,u(t)>0,t∈[0,τ2)。类似文献[10],由微分不等式比较原理和归纳法可得x1(t)>0,t≥0。考虑系统式(1)的第三个方程,积分可得:
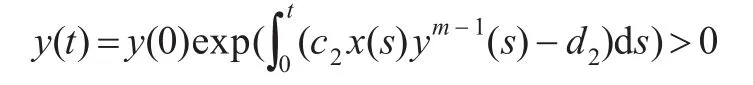
从而得到系统式(1)满足初始条件式(2)的任意解为正。
下证系统式(1)正解的有界性。令

因此可得系统式(1)的正解有界。

引理4(见文献[11])考虑微分方程 z′(t)=zm(t)(baz1-m(t)),其中a,b>0,0<m<1,z(0)>0,则

则代数方程组:
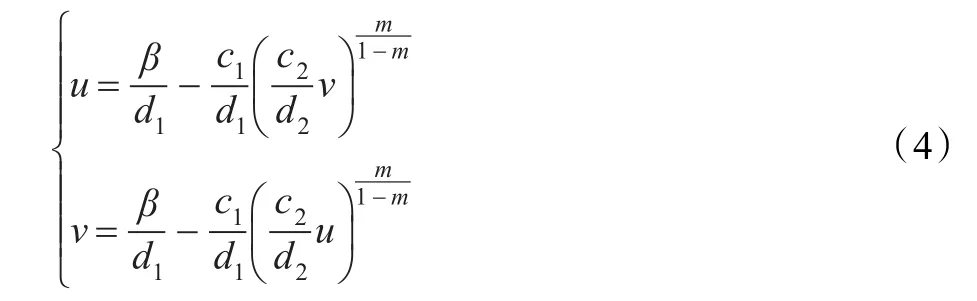
有唯一正解(x*,x*)。
3 全局吸引性
定理1若
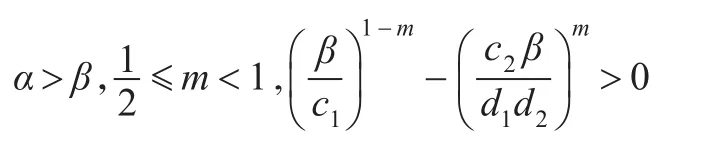
则系统式(1)在初始条件式(2)下的任意解(x1(t),x(t),y(t))满足(x1(t),x(t),y(t))=(x1*,x*,y*)。
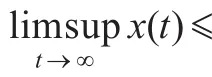

将式(5)代入系统式(1)的第三个方程得:


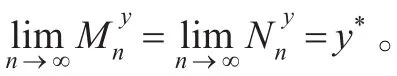
考虑系统式(1)的第一个方程,当t>0时,可得:

对式(13)两边同时取极限得:
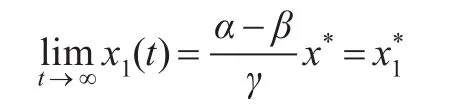
从而得到定理1的证明。
4 数值模拟
例1考虑如下系统:

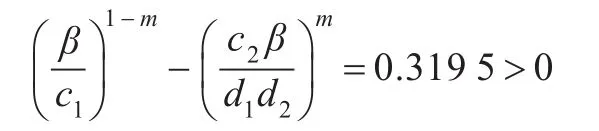
故系统式(14)满足定理1的条件。通过数值模拟(见图1,图2),可以看出在不同初始条件下系统式(14)的解皆趋向平衡态(0.626 1,0.939 2,0.416 5)。
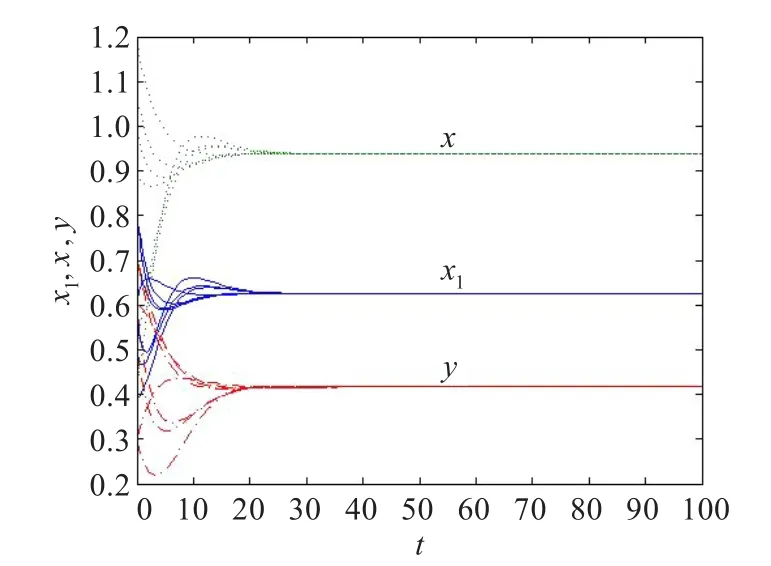
图1 系统式(14)中τ(t)=时的模拟图
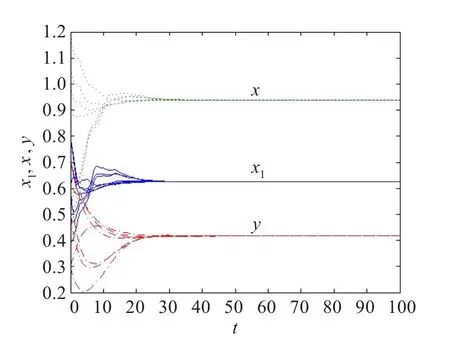
图2 系统式(14)中τ(t)=2+sint时的模拟图
5 结束语
本文主要利用微分不等式比较原理和迭代法得到了一类具有变时滞相互干扰阶段结构捕食系统平衡态全局吸引性的充分条件。该系统通过变时滞τ(t)体现了幼年食饵种群的成熟周期随着时间变化而变化。
[1]Aiello W G,Freedman H I.A time-delay model of singlepecies growth stage structure[J].Math Biosci,1990,101(2):139-153.
[2]Wang W,Chen L.A predator-prey with stage-structure for predator[J].Computer Math Appl,1997,33(3):83-91.
[3]Zhu G,Meng X,Chen L.The dynamics of a mutual interference age structured predator-prey model with time delay and impulsive perturbations on predators[J].Appl Math Comput,2010,216(1):308-316.
[4]Xu R,Chaplain M A J,Davidson F A.A Lotka-Volterra type food chain model with stage structure and time delays[J].J Math Anal Appl,2006,315(1):90-105.
[5]Xu R,Ma Z.Stability and Hopf bifurcation in a predatorprey model with stage structure for the predator[J].Nonlinear Analysis:Real World Applications,2008,9(4):1444-1460.
[6]Shi X,Zhou X,Song X.Analysis of a stage-structured predator-prey model with Crowley-Martin function[J].J Appl Math Comput,2011,36(1):459-472.
[7]Liu M,Wang K.Global stability of stage-structured predator-prey models with Beddington-DeAngelis functional response[J].Commun Nonlinear Sci Numer Simulat,2011,16(9):3792-3797.
[8]Sun X,Huo H,Ma C.Hopf bifurcation and stability in predator-prey model with a stage-structured for prey[J]. Appl Math Comput,2013,219(20):10313-10324.
[9]Kar T K,Soovoojeet J.Stability and bifurcation analysis of a stage structured predator prey model with time delay[J]. Appl Math Comput,2012,219(8):3779-3792.
[10]Song X,Chen L.Optimal harvesting and stability for a two-species competitive system with stage structure[J]. Math Biosci,2001,170(2):173-186.
[11]Wang K.Permanence and global asymptotical stability of a predator-prey model with mutual interference[J].Nonlinear Analysis:Real World Applications,2011,12(2):1062-1071.
[12]Chen F,Chen Y,Guo S,et al.Global attractivity of a generalized lotka-volterra competition model[J].Differ Equ Dyn Syst,2010,18(3):303-315.
[13]Saito Y,Takeuchi Y.A time-delay model for prey-predator growth stage structure[J].Canad Appl Math Quart,2003,11(3):293-302.
[14]Xiao Y,Chen L.Global stability of a predator-prey system with stage structure for the predator[J].Acta Math Sin:Eng Ser,2003,19(2):1-11.
[15]Song X,Chen L.A predator-prey system with stage-structured and harvesting for prey[J].Acta Math Appl Sin,2002,18(3):423-430.
WU Daiyong
School of Mathematics and Computational Science,Anqing Normal University,Anqing,Anhui 246133,China
This paper studies a mutual interference stage structured predator-prey system with varying delay.By using the comparison principle of differential inequations and an iteration scheme,a set of sufficient conditions are obtained for the global attractivity of a unique positive equilibrium of the system.An example with its numerical simulations shows the feasibility of the main results.
stage structure;mutual interference;global attractivity;predator-prey;varying delay
研究了一类具有变时滞相互干扰阶段结构捕食系统。利用微分不等式比较原理和迭代法得到了系统平衡态全局吸引的充分条件,通过举例并进行数值模拟验证了结论的可行性。
阶段结构;相互干扰;全局吸引性;捕食-被捕食;变时滞
A
O175.1;O242.1
10.3778/j.issn.1002-8331.1302-0185
WU Daiyong.Global attractivity of stage structured predator-prey system with varying delay.Computer Engineering and Applications,2014,50(24):50-53.
安徽省高等学校省级自然科学基金项目(No.KJ2013Z186,No.KJ2011A197)。
伍代勇(1979—),男,副教授,研究方向:生物数学模型及计算机仿真。E-mail:wudy9901@163.com
2013-02-27
2013-07-01
1002-8331(2014)24-0050-04
CNKI网络优先出版:2013-08-05,http∶//www.cnki.net/kcms/detail/11.2127.TP.20130805.0943.005.html

