基于神经网络补偿的机器人滑模变结构控制

李文波，王耀南

湖南大学 电气与信息工程学院，长沙 410082

基于神经网络补偿的机器人滑模变结构控制

李文波，王耀南

湖南大学 电气与信息工程学院，长沙 410082

1 引言

多关节机器人在现代工业中有着广泛的应用。作为被控对象，它有着高度非线性，高度时变，强耦合的特点，而且，它总存在着建模误差和外部干扰等不确定性，因此机器人的控制问题成为了控制领域里面的热点。滑模控制是一种对参数变化和外部干扰有着强鲁棒性的控制策略，因此，它在机器人控制领域应用很广[1-5]。文献[1-2]使用的是传统的滑模控制，文献[3-5]使用的是终端滑模控制，都获得了不错的效果。但是传统滑模控制是状态渐进收敛于平衡点，终端滑模控制则能在有限时间收敛，但当系统远离平衡点时，控制性能却不如前者。快速终端滑模控制[6]作为一种新型的滑模控制策略，结合了两者的优点，使系统状态在远离平衡点或平衡点附近都能快速收敛，并成功运用到机器人控制系统[7-10]。双幂次快速终端滑模控制[11]是在此基础上提出的改进，它具备快速终端滑模控制的所有特点，系统收敛速度更加快。但是，这方法依然没有避免大量的抖动，而且，该方法必须预先估计建模误差及不确定干扰的上界，而这难以获得，如果做过多的保守估计则会加剧抖动的产生。神经网络对任意非线性函数的逼近能力使得它得到了诸多应用[12-14]，文献[12]就使用神经网络对机器人的不确定部分进行逼近，并取得了很好的效果。本文采用了双幂次快速终端滑模控制和神经网络补偿相结合的方法，该方法采用径向基函数神经网络自适应地补偿建模误差和不确定性干扰，并通过李雅普诺夫直接法来确定权值更新，确保了系统的全局稳定性，并有效削弱了抖震，而且具有良好的暂态性能。

2 机器人动力学模型

刚性机器人数学模型常用下面的微分方程描述：

3 滑模控制器设计

4 神经网络滑模控制器设计

RBF神经网络即径向基函数神经网络（Radical Basis Function）。径向基函数神经网络是一种具有单隐层的高效的三层前馈式神经网络，它具有其他前向网络所不具有的最佳逼近性能和全局最优特性，并且网络结构简单，训练速度快。因此本文采用RBF神经网络对式（9）中不确定项进行实时逼近并予以补偿。一个输入是l维的向量x，具有m个隐含层单元，输出是n维的向量 y的RBF网络可以描述为：

将式（11）代入式（5）可得：

其中Γ∈Rm×m表示自适应速率的对角矩阵，m是隐含层单元个数。

稳定性证明：取李雅普诺夫函数为：

为避免学习过程中可能出现的φ(x)sT的值过大使得网络输出出现大的震荡，过小导致更新值趋于0，可使速率矩阵Γ为：

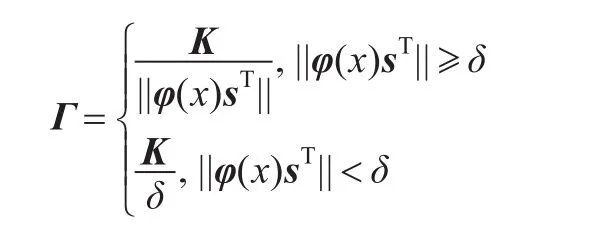
其中K是与Γ同型的对角常数矩阵，δ是避免||φ(x)sT||过小甚至为零时使得学习速率过大而设的门限值。

最后，控制系统的结构框图如图1所示。

5 仿真实验

这里选两关节机械手做仿真对象，其动力学方程为：

图1 控制结构图

机械臂的动态方程中的系统参数为r1=1 m，r2=0.8 m，m1=1.5 kg，m2=3.0 kg，J1=J2=8 kg·m 。建模误差为ΔM(q)=0.3M0(q),ΔC(q，)=0.3C0(q，)，ΔG(q)=0.3G0(q)。扰动，d=sin2(πt)+2cos(0.5πt)，增大干扰时的d=5sin2(πt)+ 10cos(0.5πt)。控制器参数为 α=2.0，β=0.8，ε=5/3，ξ= 3/5，λ=1，ϕ=1.2，μ=0.6，使用神经网络滑模控制时γ0=3.0，单纯使用滑模控制时γ0=18，神经网络有10个输入单元，7个隐含层单元，2个输出单元，隐含层基函数中心值为 C=(-3，-2，-1，0，1，2，-3)，基宽 σ=4，自适应速度对角矩阵K的对角元素全为10，δ=0.02。系统初始状态为 q1=0.8 rad/s，1=0 rad/s2，q2=1 rad/s，2= 0 rad/s2。系统期望运行轨迹为：

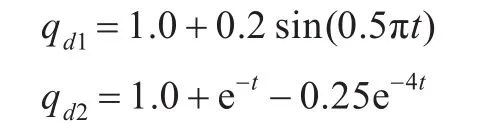
仿真结果见图2～5，其中qd1，qd2代表参考输入，q1，q2代表实际输出，u(1)，u(2)代表输出力矩，f(1)，f(2)代表实际的不确定性，fn(1)，fn(2)代表神经网络输出。

仿真结果图3表明神经网络滑模控制在对系统的建模误差和不确定性完全未知的情况下，能使系统快速地收敛于平衡点，而且相对于图2中使用的双幂次快速终端滑模控制，神经网络滑模控制大大削弱甚至避免了抖震现象。图4表明控制器在控制参数完全不变的情形下，即使加大干扰依然有良好的控制效果，验证了系统的强鲁棒性。图5显示的是神经网络对不确定性部分的良好的跟踪效果，说明了运用神经网络确实可以进行有效的补偿。

6 结束语

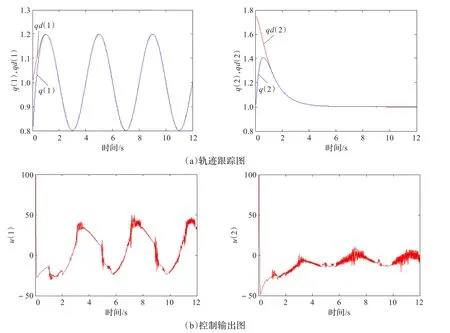
图2 双幂次快速终端滑模控制仿真结果

图3 神经网络滑模控制仿真结果

本文设计了机械手的有神经网络补偿的双幂次快速终端滑模控制方法，采用RBF神经网络逼近系统的建模误差和不确定干扰项，并通过李雅普洛夫方法设计出权值更新率，确保了全局稳定性。因此，该方法既具有双幂次型的快速收敛速度，使系统具有良好的暂态性能，又削弱甚至避免了抖动，而且增强了系统鲁棒性。最后，通过仿真实验验证了该算法具有很好的控制效果。

图4 增大干扰后神经网络滑模控制仿真结果

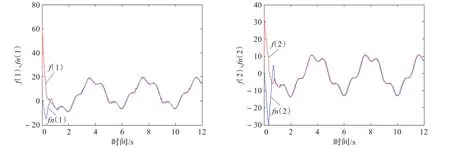
图5 神经网络跟踪结果

[1]Guo Y Z，Woo P Y.Adaptive fuzzy sliding mode controller for robotic manipulators[J].IEEE Trans on Systems，Man，and Cybernetics Part A：Systems and Humans，2003，33（2）：149-159.

[2]Su C Y，Leung T P.A sliding mode controller with bound estimation for robot manipulators[J].IEEE Trans on Robotics and Automation，1993，9（2）：208-214.

[3]Lin C K.Nonsingular terminal sliding mode control of robot manipulators using fuzzy wavelet networks[J].IEEE Trans on Fuzzy Systems，2006，14（6）：849-859.

[4]Feng Y，Yu X H，Man Z H.Non-singular terminal sliding modecontrol of rigid manipulators[J].Automatica，2002，38（12）：2159-2167.

[5]Yu T.Terminal sliding mode control for rigid robots[J]. Auomatic，1998，34（1）：51-56.

[6]Neila M B，Damak T.Adaptive terminal sliding mode control for rigid robotic manipulators[J].Automation and Comput，2011，8（2）：215-220.

[7]Yu X，Man Z.Fast terminal sliding-mode control design for nonlinear dynamical systems[J].IEEE Transactions on Circuits and Systems，2002，49（2）：261-264.

[8]Yu S H，Guo G.Global fast terminal sliding mode control forroboticmanipulators[J].International Journal of Modeling，Identification and Control，2006，1（1）：72-79.

[9]穆效江，陈阳舟.多关节机器人的神经滑模控制[J].计算机工程与应用，2009，45（11）：245-248.

[10]Hu L K，Zhao P F，Lu Z G.Trajectory tracking control based on global fast terminal sliding mode for 2-DOF manipulator[C]//The 2nd InternatianlConference on IntelligentControland Information Processing，2011：65-69.

[11]梅红，王勇.快速收敛的机器人滑模变结构控制[J].信息与控制，2009，38（5）：552-557.

[12]Feng G.A compensating scheme for robot tracking based on neural networks[J].Robotics and Autonomous Systems，1995，15（6）：100-106.

[13]Meliksah E，Okyay K.Neuro sliding mode control of robotic manipulators[J].Mechatronics，2000，10：239-263.

[14]刘金坤.机器人控制系统的设计与MATLAB仿真[M].北京：清华大学出版社，2008：31-159.

[15]Holcomb T，Morari M.Local training of radial basis function networks：towards solving the hidden unit problem[C]// Proc American Control Conf，1991：2331-2336.

LI Wenbo,WANG Yaonan

College of Electrical and Information Engineering,Hunan University,Changsha 410082,China

In this paper,fast terminal sliding mode controller with a neural network based compensator is developed for robotic manipulators with modelling uncertainties and disturbs.The two-power terminal sliding mode approach can make the system states fast converge to zero in a finite time.The neural network for compensating the uncertainties is trained on line based on Lyapunov theory and thus its convergence is guaranteed.Chattering is reduced and even eliminated.Simulation results verify the validity of the control scheme.

fast terminal sliding mode;neural network;robot;chattering

针对机器人控制系统中存在的建模误差和不确定性干扰，提出了基于神经网络补偿的滑模变结构控制。该方法采用双幂次快速终端滑模控制使得系统能在有限时间内快速达到滑模面和平衡点，采用径向基函数神经网络自适应地补偿建模误差和不确定干扰，并通过李雅普诺夫直接法设计权值更新率，确保了系统的全局稳定性，有效抑制了抖震。对两关节机器人的仿真结果表明了该方法的有效性。

快速终端滑模；神经网络；机器人；抖震

A

TP393

10.3778/j.issn.1002-8331.1303-0040

LI Wenbo,WANG Yaonan.Sliding mode variable structure control based on neural networks compensation for robotic manipulators.Computer Engineering and Applications,2014,50（23）：251-255.

国家高技术研究发展计划（863）（No.2012AA111004，No.2012AA112312）；国家自然科学基金（No.6117500075）。

李文波（1989—），男，硕士研究生，主要研究方向为机器人控制；王耀南（1957—），男，博士，教授，主要研究方向为智能机器人、智能信息处理。E-mail：liwenbo005@sina.com

2013-03-04

2013-04-01

1002-8331（2014）23-0251-05

CNKI网络优先出版：2013-04-18,http://www.cnki.net/kcms/detail/11.2127.TP.20130418.1614.006.html