基于优化配平的机翼故障飞机飞行性能分析

王 娟，刘小雄，孙 逊，唐 强

1.西北工业大学 自动化学院，西安 710072

2.西安飞行自动控制研究所，西安 710065

基于优化配平的机翼故障飞机飞行性能分析

王 娟1，刘小雄1，孙 逊2，唐 强2

1.西北工业大学 自动化学院，西安 710072

2.西安飞行自动控制研究所，西安 710065

1 引言

研究表明，飞机的飞行事故大部分是由控制失效导致的。飞机的机翼作为主要的操纵面以及产生空气动力和力矩的气动面，对飞机的飞行性能起着重要作用，当飞机的机翼发生故障时，会影响飞机产生力和力矩的特性，进而会对飞机的飞行性能产生很大的影响，机翼故障后进行性能分析对飞机故障或受损后能够安全着陆或返航有重要意义。

机翼故障打破了飞机原有的平衡，需要根据飞机新的运动学特性配平飞机。配平是一个约束优化问题，通过求解平衡点的输入与可调参数的信息，可以给驾驶员提供快速的平衡飞机方案，且可以根据平衡点信息快速估算飞行性能。已有文献进行了这类问题的研究[1-8]，文献[1]研究了故障飞机的运动方程，文献[2]对左机翼故障飞机进行性能分析研究，文献[3-5]研究了故障飞机的飞行性能，文献[6-8]对飞机进行实时状态估计、故障诊断、气动参数估计和飞行包线估算。总结已有的算法，大都采用配平技术进行故障飞机飞行性能的估算，本文提出一种基于单纯形优化的机翼故障飞机飞行性能分析方法，根据飞机爬升转弯飞行条件进行优化配平计算，由配平结果分析故障后飞机的飞行性能。应用某飞机六自由度非线性动力学模型进行仿真验证，仿真结果表明本文所提算法的有效性。

2 机翼故障建模

机翼故障将影响整个飞机的气动参数，将机翼的故障形式分为前端损伤、后缘损伤和翼面损伤，前端损伤就是沿着翼展方向翼弦被切断，通过改变机翼展长、机翼面积和平均气动弦长，从而使得力和力矩系数发生变化；若为后缘损伤，即可认为副翼损伤，通过改变副翼操纵输出设置故障；翼面损伤表示机翼表面被击穿，通过设置机翼面积的变化来实现。通过上述设置，将改变飞机方程中的力和力矩，此时飞行包线将收缩，从而改变飞机性能。

以机翼损伤为例，考虑机翼故障对飞机气动数据的影响，应用如下力和力矩方程进行研究[9-14]，根据文献[9-14]建立飞机的六自由度方程。

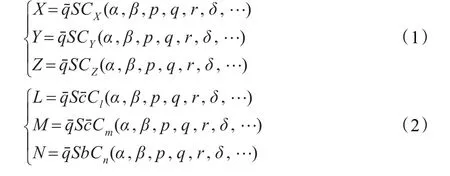
其中CX、CY和CZ表示空气动力系数，Cl、Cm和Cn表示三轴力矩系数，δ表示舵面偏转，p、q和r表示角速率，qˉ、b、S 和 cˉ分别表示动压、翼展长、机翼参考面积和平均气动弦长，α和β表示迎角和侧滑角。

机翼故障将引起飞机性能的改变，根据设定的故障，在每个飞行状态分别对系统进行配平计算，进而进行故障后的飞机性能分析。

3 基于单纯形优化方法的配平计算

配平是飞机实现控制的基础，选择机翼损伤或故障后的飞行条件为稳态爬升转弯飞行。根据非线性优化在每个飞行状态进行配平计算，则可得到不同故障下的配平数据库。

3.1 配平条件

刚体飞机六自由度非线性方程可以简写为x˙=f(x，u)，12维状态向量 xT=[ρTνT]可以分为两个向量，描述飞机位置和姿态的向量 ρT=[x y h ϕ θ ψ]和描述飞机速度的向量 νT=[VTα β p q r]。

配平状态就是稳定的飞行状态。此时，稳态爬升转弯飞行条件由下列状态方程决定：

3.2 可变单纯形优化算法

为了求出上述一系列的配平状态，根据稳态爬升转弯飞行的条件，应用有约束的非线性约束优化得到将上述问题的数学模型如下：

objtrim(x，u)为优化目标函数，Q为任意镇定矩阵，s.t.为约束条件。其中：

a=cosαcosβ，b=sinφ sinβ+cosφ sinαcosβ，配平的航迹倾斜角 γ*满足关系式式（5）中前两个约束式直接限制飞机的高度和空速，第三个约束式间接指定所需爬升率，而最后三个约束间接指定所需转弯率，此时，可得爬升转弯飞行条件下反应飞行性能的爬升率和转弯率：

s(u)为控制输入限制集合，包括发动机推力T以及升降舵偏转ue、方向舵偏转ur和副翼偏转ua：

根据上面的关系，可以进行平衡点的求解，求解有约束的非线性最优化问题的方法有很多，本文选用经典的优化方法可变单纯形法。

可变单纯形法的基本思想是[15]：给定 Rn中一个单纯形，这里的单纯形指的是n维欧式空间Rn中具有n+1个顶点的凸多面体，其中n为迭代的独立变量的个数，本文中n=7；求出n+1个顶点的函数值，并确定这些函数值中的最大值、次大值和最小值；通过反射、扩张、收缩求出一个较好点并取代最大值点，构成新的单纯形；多次迭代逼近极小值点，迭代中逐渐把单纯形向最优点移动。

具体步骤如下（令objtrim(x，u)=O）：

（1）给定初始单纯形，置循环变量k=1。配平独立变量z0=[utueuruaα β ϕ]T，在每个变量的取值范围内任意给定初值z0=[5 000-0.09-0.01 0.01 8.49 0 0]T。Z=[zy]=[z(1)，z(2)，…，z(n+1)] 为单纯形矩阵，y是由 z0000构造的n×n维对角矩阵，若z0中第i个元素z0(i)非零，则用(1 +0.05) z0(i)代替 y0对角线上的第i个元素，反之用 0.000 25 代替。z(1)，z(2)，…，z(n+1)即为 Rn中的 n+1个顶点。

（3）确定有利的搜索方向。单纯形法认为，极小点在最大值点与其余点的形心的连接线上的可能性较大，此方法力图在上述方向上找到一个较好点。

（4）给定反射系数 μ1=1 6，扩展系数 μ2=2，压缩系数 μ3=0.5。

（9）检验是否满足收敛标准。若O＜ε（这里令ε= 10-7），则停止计算，将现行最好点作为极小点的近似；否则置 k′=k+1，返回步骤（2）。

上述步骤都是在给定的某个飞行状态(h*，VT*，h˙*，ψ˙*)下进行的，若得到的优化解同时满足控制输入的约束条件，则可认为 x*和u*是objtrim(x，u)最小化的解，则给定的飞行状态可以配平，将其列入D中；若在控制输入的约束范围内没有找到优化解，则给定的这个飞行状态不能配平，也就不将其列入D中。

4 机翼故障飞机基本性能的分析

飞机故障后主要关心其稳定性和可控性，以及爬升率和转弯率等飞行性能。首先将飞机的运动学方程 线 性 化 为则 配 平 状 态的 线 性 小 扰 动模型可表示为k=AKxk+Bkuk，若可控性矩阵UC=行满秩，则可认为飞机在的邻域内可控。若相应配平状态下线性小扰动系统的所有特征根在左半平面内即 R{λi(Ak)}＜0，i=1，2，…，8，则飞机在该配平状态是自然稳定的；如果系统存在非自然稳定的配平状态，且该状态可控，则可以设计控制器uk=-Kkxk使该类状态转变为稳定的配平状态，进而增加了配平数据库中的可用状态个数。根据式（6）、（7）计算飞机的爬升率和转弯率，进而得到飞机的基本飞行性能。

飞机故障后，紧急飞行规划可以调用故障后的配平数据库来规划出着陆或返航的飞行轨迹。事实上，配平数据库是对飞行性能约束的一种离散表述。配平数据库中的数据越丰富，越有利于故障飞机选择合适的配平状态指引故障飞机着陆或返航；反之，则表明故障飞机的飞行性能明显退化，此时可以选择的配平状态有限，进而将影响飞机在着陆或返航过程中的飞行轨迹。因此建立的配平数据库中，爬升率和转弯率都应该包含正值、零和负值三种情况，即可实现爬升、下降、左/右转弯等多种飞行状态。和有限的转弯性能相比，广泛的爬升率可以使故障飞机尽可能地根据着陆或返航要求改变飞行高度。

5 仿真分析

应用某飞机六自由度运动方程进行仿真分析。全部配平数据是在一组爬升转弯飞行条件下定义的，每一个飞行条件都是由表1中的数据组合决定。为了实现D的可视化，可以固定配平状态四个元素中的一个，本文为 h ，则简化为 (VT，，)。

表1 离散飞行条件

根据机翼故障模型和表1绘出三种故障下的D，三个坐标分别为爬升率（CR）、转弯率（TR）和空速（V）。对前端损伤，设翼展损失30%，则机翼面积和平均气动弦长也发生变化，D如图1所示；对后缘损伤，设副翼卡死在10°，则气动系数 CYδa=Cnδa=Clδa=0，副翼输出 δa≡ 10°，此时从原来用于单纯形算法的8个独立变量中应去掉ua，D如图2所示；对翼面损伤，设机翼面积损伤30%，D如图3所示。图中蓝色的点表示自然稳定的配平状态，绿色的点表示非自然稳定但可控的配平状态，没有颜色标记的区域代表不能配平的飞行条件以及非自然稳定且不可控的配平状态。

由图1和图3可以看出，机翼前端损伤或翼面损伤后，几乎所有的力和力矩均受到影响，低空时，飞机容易配平且比较稳定，非自然稳定的配平状态比较分散；当飞行高度在10 010～20 010 ft时，飞机非自然稳定的配平状态主要集中在大转弯率且低空速区域；当高空高速飞行时，转弯率越大飞机越不稳定。

由图2可以看出，副翼卡死后影响侧力、俯仰力矩和偏航力矩，飞机的偏航运动和滚转运动受限较多，高于20 010 ft时，转弯率越大飞机越不稳定。

图1 机翼前端损伤30%

图2 机翼后缘损伤-副翼卡死在10°

图3 翼面损伤30%

综合图1～3可以看出，机翼受损或故障后，随着高度的增加，配平数据库在三维方向均收缩，非自然稳定的配平状态越来越多且主要集中在大转弯区域，这主要是因为故障飞机受到的气流扰动随高度增加而增大，垂直气流影响α，水平气流影响 β，进而影响故障飞机的力和力矩系数，飞机的机动性和稳定性均变差；空速较低时，飞机不易配平，因为较高的空速可以弥补由机翼损伤而损失的升力；飞机具有广泛的爬升率。

6 结束语

飞机机翼作为产生力和力矩的主要部件对飞行性能起着重要的作用，分析机翼故障对飞行性能的影响对提高飞行安全具有重要意义。本文提出一种机翼故障飞机飞行性能分析方法，根据飞机爬升转弯飞行条件进行优化配平计算，建立机翼故障后的飞机平衡点，根据平衡点信息分析故障后飞机的飞行性能。仿真结果表明本文所提算法的有效性。本文的方法拓宽了容错飞行控制系统的研究领域。

[1]Bacon B J，Gregory I M.General equations of motion for a damaged asymmetric aircraft[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit，Hilton Head，South Carolina，2007.

[2]TangYunshen，AtkinsE M，SannerR M.Emergency flight planning for a generalized transport aircraft with leftwingdamage[C]//AIAA Guidance，Navigationand Control Conference and Exhibit，Hilton Head，South Carolina，2007.

[3]Strube M J，Sanner R M，Atkins E M.Dynamic flight guidance recalibration after actuator failure[C]//AIAA 1st Intelligent Systems Technical Conference，Chicago，Illinois，2004.

[4]Strube M J.Post-failure trajectory planning from feasible trim state[D].[S.l.]：University of Maryland，2005.

[5]Choi H，Atkins E M.Flight envelope discovery for damage resilience with application to an F-16[C]//Infotech@Aerospace 2010，Atlanta，Georgia，2010.

[6]Dongmo J E T.Aircraft loss-of-control recovery using nonlinear smooth feedback regulators[C]//Infotech@Aerospace 2011，St Louis，Missouri，2011.

[7]Urnes J M，Reichenbach E，Smith T.Dynamic flight envelope assessment and prediction[C]//AIAA Guidance，Navigation and Control Conference and Exhibit，Honolulu，Hawaii，2008.

[8]Tang Liang，Roemer M，Ge Jianhua.Methodologies for adaptive flight envelope estimation and protection[C]// AIAA Guidance，Navigation，and ControlConference，Chicago，Illinois，2009.

[9]Morelli E A，Smith M S.Real-time dynamic modelingdata information requirements and flight test results[C]// AIAA AtmosphericFlightMechanicsConferenceand Exhibit，2008.

[10]Pandita R，Chakraborty A，Seiler P，et al.Reachability and region of attraction analysis applied to GTM dynamic flight envelope assessment[C]//AIAA Guidance，Navigation，and Control Conference，2009.

[11]刘小雄，邱岳恒，刘世民，等.操纵面故障对飞行包线的影响研究[J].飞行力学，2012，30（2）：128-131.

[12]方振平，陈万春，张曙光.航空飞行器飞行动力学[M].北京：北京航空航天大学出版社，2008：128-136.

[13]刘晓明，苏彬，孙宏.飞行性能与计划[M].成都：西南交通大学出版社，2003：5-17.

[14]Stevens B L，Lewis F L.Aircraft control and simulation[M]. New York：Wiley-Interscience，1992.

[15]何春雄，潘少华，蒋金山.最优化计算方法[M].广州：华南理工大学出版社，2007：124-128.

WANG Juan1,LIU Xiaoxiong1,SUN Xun2,TANG Qiang2

1.School of Automation,Northwestern Polytechnical University,Xi’an 710072,China
2.Flight Automatic Control Research Institute,Xi’an 710065,China

The wings of aircraft play an important role on the aircraft,so analysis of flight performance of wing faults is of significance for aircraft safe landing.This paper presents an analyzing method for the flight performance of fault aircraft,which is based on the Nelder-Mead optimization trimming.The wing fault parameter model is established.Then the aircraft is trimmed according to climbing turn flight conditions,and the trim databases are obtained in wing fault parameter modes on different flight conditions,and the basic flight performance is analyzed.The simulation results show the effectiveness of the proposed method.

wing fault;Nelder-Mead optimization;climbing and turning;trim databases;flight performance

分析飞机机翼故障对飞行性能的影响，对飞机故障后能够安全着陆或返航有着重要意义，飞机的机翼作为产生力和力矩的主要部件对飞行性能起着重要的作用。提出一种基于单纯形优化的机翼故障飞机飞行性能分析方法，建立机翼故障参数模型，根据飞机爬升转弯飞行条件进行优化配平计算，得到在不同状态下不同机翼故障的配平数据库，分析了故障后飞机的飞行性能。仿真结果表明所提算法的有效性。

机翼故障；单纯形优化；爬升转弯；配平数据库；飞行性能

A

V249.1

10.3778/j.issn.1002-8331.1301-0301

WANG Juan,LIU Xiaoxiong,SUN Xun,et al.Flight performance analysis for aircraft with wing faults based on optimization of trimming.Computer Engineering and Applications,2014,50（23）：229-233.

航空科学基金资助（No.20100753009）。

王娟（1987—），女，硕士，研究方向为飞行控制与仿真；刘小雄（1973—），男，博士，副教授，研究方向为飞行控制与仿真、故障诊断与容错控制；孙逊（1982—），男，博士，研究方向为飞行控制技术；唐强（1978—），男，博士，研究方向为飞行控制与仿真。E-mail：xwj19871114@163.com

2013-01-28

2013-05-06

1002-8331（2014）23-0229-05

CNKI网络优先出版：2013-05-24,http://www.cnki.net/kcms/detail/11.2127.TP.20130524.1509.004.html