最小二乘双支持向量回归机

卢振兴，杨志霞，高新豫

新疆大学 数学与系统科学学院，乌鲁木齐 830046

最小二乘双支持向量回归机

卢振兴，杨志霞，高新豫

新疆大学 数学与系统科学学院，乌鲁木齐 830046

1 引言

支持向量机（Support Vector Machine，SVM）[1-2]主要用于解决分类问题和回归问题[3-4]。它是基于结构风险最小化原则[2]的一种方法，在机器学习领域中备受关注，近些年得到了飞速的发展。然而，基于支持向量机的回归算法，并不像分类算法发展得那么完善。目前基于支持向量机的回归算法主要有支持向量回归机[5]（Support Vector Regression，SVR）、最小二乘支持向量回归机[6-7]（Least Square Support Vector Regression，LSSVR）和双支持向量回归机[8]（Twin Support Vector Regression，TWSVR）等。传统的支持向量回归机是通过求解一个二次规划问题来得到最终的回归函数，计算复杂度相对较高。最小二乘支持向量回归机只需求解一个线性方程组，其计算复杂度比传统的支持向量回归机降低了很多。2009年，文献[8]提出了双支持向量回归机。它是受双支持向量分类机[9]的启发，不像传统支持向量机用两个平行超平面构造回归函数，而是用两个非平行超平面构造回归函数，因此双支持向量回归机具有更好的推广能力。双支持向量机的另一个优点是通过求解两个较小规模的二次规划得到最终的回归函数，比传统支持向量回归机的计算复杂度低。

本文提出了最小二乘双支持向量回归机（Least Square Twin Support Vector Regression，LSTSVR），它整合了最小二乘思想和双支持向量回归机的思想，即在双支持向量回归机的基础之上加入了最小二乘的思想，同样是通过两个非平行平面构造最终的回归函数。不同的是，最小二乘双支持向量回归机只需解两个较小规模的线性方程组就能得到最终的回归函数，而不是像双支持向量回归机那样求解两个二次规划，这样就大大降低了计算复杂度。数值实验表明，最小二乘双支持向量回归机不仅计算速度快，而且有更好的预测精度。

2 背景知识

首先给出回归问题的数学描述，给定训练集：

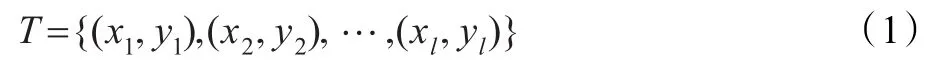
其中 xi∈Rn是输入，yi∈R是输出，i=1，2，…，l。

在本文中，用X表示由所有的输入xi构成的矩阵，Y表示由所有的输出 yi构成的列向量。本文的任务是找到如下的回归函数[10]：

传统的支持向量回归机的思想源于支持向量分类机，它利用最大间隔的思想，通过结构风险最小化原则建立了一个二次规划的原始问题，通常求解其对偶问题[11]来得到原始问题的解，即可得式（2）。当引入核函数[12]后，很容易将线性模型扩展到非线性模型。

文献[6-7]中提出了最小二乘支持向量回归机，它主要是将最小二乘的思想融入到支持向量回归机的模型中，其思想源于最小二乘支持向量分类机[7]，用等式约束代替传统的支持向量回归机中的不等式约束，从而只需解一组线性方程组就可以得到问题的解，即可得到式（2），花费的时间大大减少，计算成本也相应降低，所以常被用于解决样本点规模较大的问题。

双支持向量回归机于2009年在文献[8]中被提出，它的灵感来源于双支持向量分类机[9]。双支持向量回归机需要找到两个非平行超平面，称之为上界和下界回归函数。

双支持向量回归机由下面两个优化问题构成：

3 最小二乘双支持向量回归机

这一章提出了一个新的回归算法，它的思想来源于双支持向量回归机，称它为最小二乘双支持向量回归机，是将最小二乘的思想运用到双支持向量回归机中而建立的。

3.1 线性情形

考虑线性情形，最小二乘双支持向量机的原始优化问题为：

其中 C1，C2＞0 是惩罚参数，ε1，ε2＞0 是 ε不敏感损失函数[11]的参数，ξ，η是松弛因子。最小二乘双支持向量回归机的目的是找到两个函数来构造最终的回归函数。首先，在问题（7）～（8）的目标函数中，第一项表示极小化样本点到超平面f1(x)=0的距离，第二项是极小化误差。应当指出，由于误差项是平方项，所以不需要限定松弛变量ξ，η非负。约束条件表示让样本点尽量地围绕在超平面 f1(x)=0的ε1不敏感下界超平面，即 f1(x)-ε1=0的周围。直观的几何解释如图1所示。两个超平面 f1(x)=0与 f1(x)-ε1=0之间的带子类似于标准支持向量回归机的半ε1带。对于问题（9）～（10）有相似的解释，只是超平面 f2(x)=0决定了它的上界ε2不敏感上界超平面 f2(x)+ε2=0，它们之间构成了另外一个半ε2带。

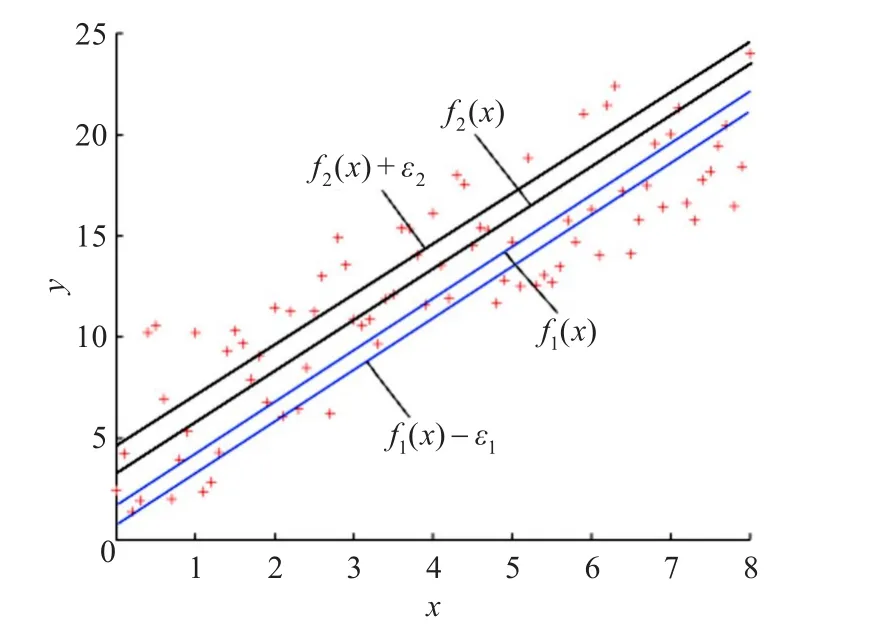
图1 最小二乘双支持向量回归机几何解释

为了求解问题（7）～（8），可将约束条件代入目标函数中得到如下的拉格朗日函数：

最小二乘双支持向量机的线性情形求解过程具体可见流程图2。

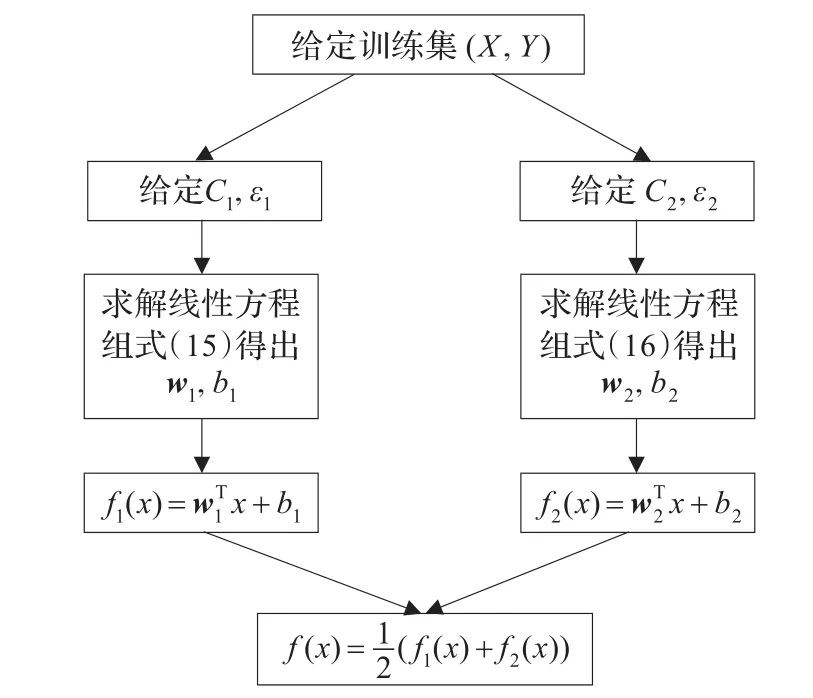
图2 最小二乘双支持向量回归机流程框图

3.2 非线性情形

根据线性最小二乘双支持向量回归机的思想，下面来考虑非线性最小二乘双支持向量回归机，其任务是求解如下两个非线性超平面，即 f1(x)=uT1K(X，x)+γ1和f2(x)=uT2K(X，x)+γ2为了得到这两个超平面建立如下两个优化问题：

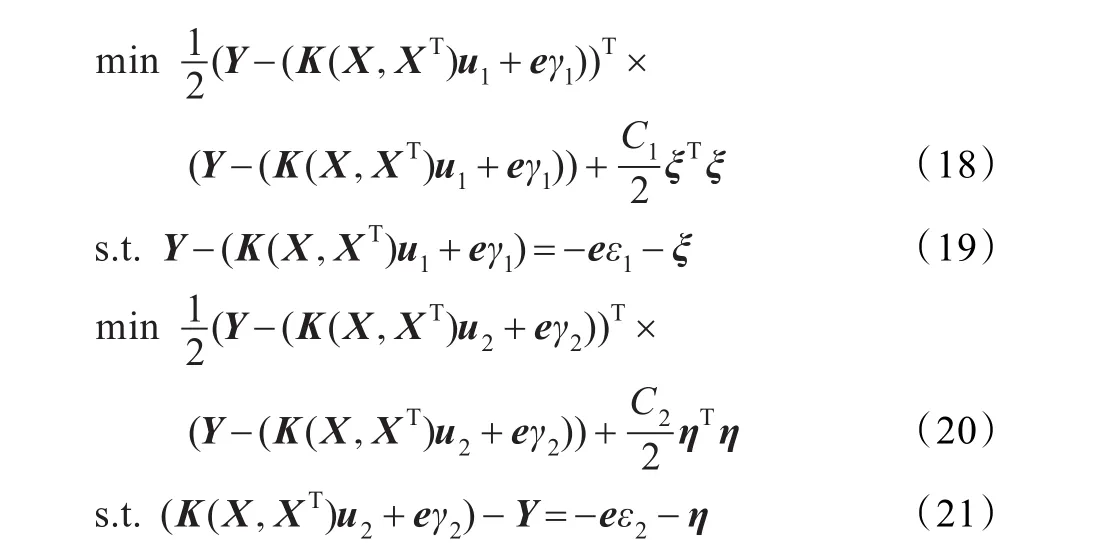
其中 C1，C2＞0 是惩罚参数，ε1，ε2＞0 是 ε不敏感损失函数的参数，ξ，η是松弛因子。将问题（18）～（19）的约束条件代入目标函数可得：

从上面可以看出，对于非线性情况，只需引入核函数就可以得到问题的解，非线性问题的流程图与线性的不同就是所要求解的线性方程组不同，即非线性情况需求解线性方程组式（26）和式（27），且得出的 f1(x)=

4 实验与讨论

为了检验最小二乘双支持向量归机，并与支持向量回归机、最小二乘支持向量回归机和双支持向量回归机作对比，利用了人工数据和UCI数据库中的几个数据。在实验中参数均选自于集合{2i|i=-8，…，8}，同时令C1=C2，ε1= ε2，并通过十折交叉检验法[12]来选取参数。文中核函数定为高斯核 K(u，v)=exp(-‖u-v‖2/2p21)，为了缩减选择参数的时间，令参数 p1=1。数值实验在Windows 7系统上完成，处理器为英特尔酷睿双核，主频为2.2 GHz，内存为2 GB。程序编辑基于Matlab R2010a平台上完成。并且所有的算法都使用的是Matlab中的求解二次规划和线性方程组的函数。

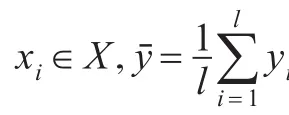
4.1 人工数据实验

在这个数值实验中，用最小二乘双支持向量回归机去逼近函数sinc(x)，函数定义为：

对这个函数加入一个噪音，会产生一组新的样本点，这里只用到两种噪音，定义这组数据(xi，yi)，如下：i=1，2，…，200，U[a，b]表示在区间 [a，b]之间产生一组随机的数，记式（30）中的 ξi为noise1，记式（31）中的 ξi为noise2。

表1中列出了在两种不同噪声的扰动下最小二乘双支持向量回归机和双支持向量回归机的回归效果，其中最好的结果由黑体表示。在实验中，对每个数据进行了10次10折交叉过程，最后的结果由10次数据结果的平均值加减方差构成，表1中可以看出最小二乘双支持向量回归机能够得到最小的SSE/SST最大的SSR/SST，对比数据结果中±后的方差可以看出，最小二乘双支持向量回归机得到的方差均小于双支持向量回归机，说明最小二乘双支持向量回归机预测相对比较稳定，更接近于真实值，由于求解最小二乘双支持向量回归机只需要解两组线性方程组，所以它的运算时间也明显少于双支持向量回归机。从图3、图4中可以直观地看出来，在这两个噪声的扰动下，最小二乘双支持向量回归机的回归效果较好。

表1 在噪音noise1、noise2扰动下，TSVR和LSTSVR对函数sinc(x)的回归效果

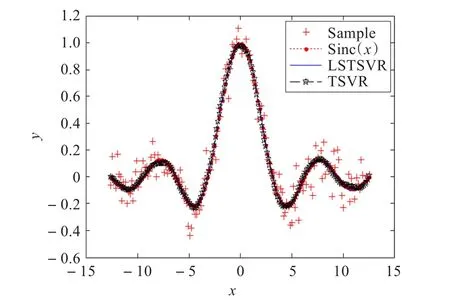
图3 在noise1扰动下TSVR，LSTSVR的回归效果

图4 在noise2扰动下TSVR，LSTSVR的回归效果

表2 LSTSVR、TSVR、LSSVR在7组UCI数据中的表现

4.2 UCI数据

在实验中，利用UCI数据中的7个数据来做数值实验，包括 Boston housing、Machine CPU、Auto price、Concrete Compressive Strength、Wisconsin Breast Cancer、Motorcycle、Auto-Mpg，这些数据经常会被用来检测回归算法的优劣。具体地，Boston housing数据包括506个样本，每个样本有13个特征，Machine CPU是反映计算机中CPU表现的一组数据，它包含209个样本，每个样本点含有7个特征，Auto price由159个样本点构成，每个样本点有15个特征，Motorcycle中含有133个样本，Auto-Mpg包含398个样本点，每个样本点有7个特征，Concrete Compressive Strength中含有1 030个样本点，Wisconsin Breast Cancer中拥有699个样本点，其中每个样本点都有10个特征。

在UCI数据实验中，同样对每个数据做10次10折交叉过程，最终的结果由10次实验结果的平均值加减方差构成，这样的结果既可以说明预测精度的高低，又可以说明算法预测的稳定性。表2中给出了具体的数值结果，其中表现最好的用黑体表示。从表2可以看出，在时间上，最小二乘双支持向量回归机占绝对优势，其计算时间均远远小于其他所有算法，相比于最小二乘支持向量回归机，它将原来的规模较大的线性方程组变为两个规模较小的线性方程组来解，其时间大大缩短了。就精度而言，只有双支持向量回归机的精度可以与它相媲美，7组数据结果中，双支持向量机两个SSE/SST的值小于最小二乘双支持向量回归机，其他算法的精度均远远不如它，只有在Auto-Mpg这一数据中，支持向量机得到了最小的SSE/SST，但计算时间方法却远远优于其他的回归算法，在表2中，最小二乘双支持向量机算出数据Auto Price和Wisconsin B.C最小的SSE/SST和最大的SSR/SST，最小二乘双支持向量回归机得到的大部分的SSE/SST都比其他算法所得的小，同时可以看出最小二乘双支持向量回归机的预测稳定性也相对较好，足以说明最小二乘双支持向量回归机比其他算法更高效，精度更高，而且有很好的推广能力。

5 结束语

在本文中，提出了最小二乘双支持向量回归机，求解它只需解两个较小规模的线性方程组，而不同于双支持向量回归机中求解两个二次规划问题，更不像支持向量回归中求解一个大规模的二次规划问题，它的灵感来源于双支持向量回归机，对双支持向量回归机的模型加入了最小二乘的思想，在约束条件里只有等式约束，所以在求解时只需将约束条件代入到目标问题中，这样只需要解两个线性方程组。因此它显然继承了双支持向量回归机和最小二乘支持向量回归机的优点，并且优于它们。对于未来的研究中，应该致力于特征选择来减少计算代价，才能更有利于支持向量机进一步的发展。

[1]Vapnik V N.The natural of statistical learning theory[M]. New York：Springer，1995.

[2]Vapnik V N.Statistical learning theory[M].New York：Wiley，1998.

[3]Burges C J.A tutorial on support vector machines for pattern recognition[J].Data Mining Knowledge Discovery，1998，2（2）：121-167.

[4]Christianini V.Shawe-Taylor J.An introduction to support vector machines[M].Cambridge：Cambridge University Press，2002.

[5]Smola A J，Scholkopf B.A tutorial on support vector regression[J].Statistics and Computing，2004，14（3）：199-222.

[6]Suykens J A K，Tony V G，Jos D B，et al.Least squares supportvectormachines[M].Singapore：World Scientific Pub Co，2002.

[7]Suykens J A K，Vandewalle J.Least squares support vector machine classifiers[J].Neural Process Letter，1999，9（3）：293-300.

[8]Peng X.TSVR：an efficient twin support vector machine for regression[J].Neural Networks，2009，23：356-372.

[9]Jayadeva，Khemchandani R，Chandra S.Twin support vector machines for pattern classification[J].IEEE Trans on Pattern Anal Mach Intell，2007，29：905-910.

[10]业宁，梁作鹏，董逸生，等.一种SVM非线性回归算法[J].计算机工程，2005，31（20）：19-21.

[11]邓乃扬，田英杰.数据挖掘中的新方法-支持向量机[M].北京：科学出版社，2004.

[12]邓乃扬，田英杰.支持向量机-理论、算法与拓展[M].北京：科学出版社，2009.

[13]Allen D M.The relationship between variable selection and prediction[J].Technometrics，1974，16：125-127.

[14]Weisberg S.Applied linear regression[M].New York：Wiley，1985.

[15]Bates D M，Watts D G.Nonlinear regression analysis and its applications[M].New York：Wiley，1988.

LU Zhenxing,YANG Zhixia,GAO Xinyu

College of Mathematics and System Sciences,Xinjiang University,Urumqi 830046,China

In this paper Least Square Twin Support Vector Regression（LSTSVR）is proposed,which is formulated via the idea of Twin Support Vector Regression（TSVR）.LSTSVR breaks the idea which ε-band is constructed by two parallel hyperplanes in traditional Support Vector Regression（SVR）.Actually,LSTVR employes two non-parallel hyperplanes to construct the ε-band,in which each hyperplane determinates a halfε-bond,and obtain the final regression.So the regression function fits the distribution of dataset and the algorithm has better generalization ability.In addition,in LSTSVR, the main computing cost is to solve two smaller systems of linear equations,so the computational complexity is low.The experimental results indicate that the proposed algorithm has certain advantage in generalization ability and computational efficiency.

regression problem;support vector regression;twin support vector regression;least square twin support vector regression

提出了一个最小二乘双支持向量回归机，它是在双支持向量回归机基础之上建立的，打破了标准支持向量回归机利用两条平行超平面构造ε带的思想。事实上，它是利用两条不一定平行的超平面构造ε带，每条超平面确定一个半ε-带，从而得到最终的回归函数，这使该回归函数更符合数据本身的分布情况，回归算法有更好的推广能力。另外，最小二乘双支持向量机只需求解两个较小规模的线性方程组就能得到最后的回归函数，其计算复杂度相对较低。数值实验也表明该回归算法在推广能力和计算效率上有一定的优势。

回归问题；支持向量回归机；双支持向量回归机；最小二乘双支持向量回归机

A

O235

10.3778/j.issn.1002-8331.1301-0136

LU Zhenxing,YANG Zhixia,GAO Xinyu.Least square twin support vector regression.Computer Engineering and Applications,2014,50（23）：140-144.

国家自然科学基金（No.11161045）。

卢振兴（1985—），男，硕士研究生，研究领域为支持向量机；杨志霞（1977—），通讯作者，女，博士，副教授，研究方向为最优化方法、支持向量机；高新豫（1988—），女，硕士研究生，研究领域为支持向量机。E-mail：yangzhixia@gmail.com

2013-01-14

2013-03-25

1002-8331（2014）23-0140-05

CNKI网络优先出版：2013-04-26,http://www.cnki.net/kcms/detail/11.2127.TP.20130426.1018.010.html