基于区域序列枚举法的蜂巢数独求解算法研究

肖华勇，杨菲菲，黄奔茹

西北工业大学 理学院 数学系，西安 710129

基于区域序列枚举法的蜂巢数独求解算法研究

肖华勇，杨菲菲，黄奔茹

西北工业大学 理学院 数学系，西安 710129

1 引言

数独（Sudoku）是一种基于逻辑推理的数学谜题，是18世纪末由瑞士数学家欧拉发明的，后在美国发展，并在日本得以发扬光大。数独的玩法逻辑上非常简单，但数字排列方式千变万化。谜题中会预先填入若干数字，其他宫格为空白，玩家需要根据谜题中的数字分布状况，逻辑推敲出剩余的空格所需数字。随着对数独研究的深入，出现了越来越多的变形，数独形状变化（蜂巢数独、环状数独等）和引入和式计算（Killer数独、Kakuro数独等）等[1]。

蜂巢数独是标准数独形状发生变化的数独，其外形类似蜂巢，所以称为蜂巢数独。如图1所示，蜂巢数独有行，没有列和九宫格，但有正斜线、反斜线。它要求每行、正斜线、反斜线所填数字不能重复，且每行、正斜线、反斜线所填数字序列是连续数列（例如 1～6，3～8，4～9，…）。除了中间的行、正斜线、反斜线所填数字是1～9，其他行、正斜线、反斜线所填数字不一定是从1开始，也就是说其他行、正斜线、反斜线所填数字不一定包括1～9这9个数字。由于蜂巢数独并没有九宫，最特殊的是蜂巢连线（行、正斜线、反斜线）数字序并不固定，所以不能完全沿用传统数独解题技法。

国内外学者针对数独求解方面展开了大量研究，他们把数独问题转化成不同的数学模型。A.C.Bartlett等[2-3]针对对角线数独、金字塔数独等特殊形式的数独建立了0-1整数规划模型，并运用Matlab中的优化函数求得模型的解。肖华勇等[4]提出了用数独规则的逐步枚举算法求解标准数独，该方法比回溯法具有更快的速度。Christian Posthoff等[5]用建立逻辑方程的形式求解数独谜题，但是这种算法的效率比较低。刘延风等[6]用遗传算法求解标准数独。Sheehan Khan等[7]用概率图解方法求解数独，但是其算法的适应性、通用性不高。J. Goldberger[8]对信息传递算法进行了改进，使之适用于一般的数独问题。Lynce等[9]用两种SAT推理方法解决了数独谜题。J.A.Bondy等[10]将数独问题转化为着色问题。肖华勇等[11]研究了标准数独的方程求解算法问题。R.Lewis[12]提出利用现代优化算法求解标准数独问题，并提出了一种基于模拟退火的求解方法。但是以上文献多针对标准数独展开研究，而对于蜂巢数独等变形数独的研究较少。

图1 初级蜂巢数独谜题

目前国内外学者对于蜂巢数独的研究多局限于行列唯一法、基本摒除法、三角形摒除法、余数法、数偶法、砂漏法等直观法求解[13]，与标准数独的直观法求解[14]有很大的不同。但是对计算机求解蜂巢数独的算法的研究尚属起步阶段。

蜂巢数独同标准数独最大的区别在于形状类似蜂巢，完全抛弃了九宫格，对序列有连续性的要求。因此在求解算法上，两者相似但有很大的不同。本文利用线性规划方程组建立数学模型，研究其解的性质，然后提出算法，并用实例说明求解的有效性。

2 线性规划模型的建立

2.1 单元格的表示

蜂巢数独的行对应标准数独的行，正斜线表示数独从左到右从右上到左下的9条斜线，反斜线表示数独从左到右从左上到右下的9条斜线。

每个单元格用坐标(i，j)表示。i代表行号，从上到下 i=1，2，…，9 ；j代表列号，从左到右为 1，2，3，… 。其中第1行 j=1，2，…，5，第2行 j=1，2，…，6，依次类推，第9行 j=1，2，…，5。

用 Ai(i=1，2，…，9)表示每行存放的单元格的集合 。其 中 A1={(1，1)，(1，2)，(1，3)，(1，4)，(1，5)}，A2={(2，1)，(2，2)，(2，3)，(2，4)，(2，5)，(2，6)}，以此类推 A9={(9，1)，(9，2)，(9，3)，(9，4)，(9，5)}。

用Bi(i=1，2，…，9)表示每条正斜线存放的单元格的集合，每条正斜线上的单元格按从上到下排列。

其 中 B1={(1，1)，(2，1)，(3，1)，(4，1)，(5，1)}，B2={(1，2)，(2，2)，(3，2)，(4，2)，(5，2)，(6，1)} 以此类推 B9={(5，9)，(6，8)，(7，7)，(8，6)，(9，5)}。

用Ci(i=1，2，…，9)表示每条反斜线存放的单元格的集合，每条反斜线上的单元格按从上到下排列。

其 中 C1={(5，1)，(6，1)，(7，1)，(8，1)，(9，1)}，C2={(4，1)，(5，2)，(6，2)，(7，2)，(8，2)，(9，2)}，以此类推 C9={(1，5)，(2，6)，(3，7)，(4，8)，(5，9)}。

每个单元格有其所在的行号，正斜线号和反斜线号。每个单元格用一个三维向量(u，v，w)表示。如单元格 (1，1)的三维向量为 (1，1，5)，它表示单元格 (1，1)是第1行，第1条正斜线和第5条反斜线相交的单元格。

2.2 区候选数的确定

由于除了中间的行、正斜线、反斜线所填数字是1～9，其他行、正斜线、反斜线所填数字不一定包括1～9这9个数字。所以它不能像标准数独那样让空单元格的初始候选数取1～9这9个数字，它要按各行所含有的单元格数和已填数字来确定初始候选数。

为方便起见，把某行、某正斜线、某反斜线都称为一个区。设某区有L个格子，则该区只允许L个连续数字。若该区所填数字单元格大于1个时，取所填数字中最小数字为a，最大数字为b；若该区所填数字单元格只有一个时，a取该单元格的值，且b=a；则该区候选数范围为 [m，M]，其中 m=max{1，b-L+1}，M=min{9，a+L-1}。当该区一个数字也没有填，取m=1，M=9。由于该区所填数字是L个连续数字，这连续数字序列可能为 [m，m+L-1]，或 [m+1，m+L]，…，或 [M-L+1，M]，则该区必然出现的候选数为这些连续数字序列的交集[M+(1-L)，m+(1-L)]。各区必然出现的候选数用L(At)，L(Bt)，L(Ct)表示，其中 t=1，2，…，9 。

如图1，第一行 a=6，b=7，L=5，则第一行候选数范围为 [3，9]，5 个连续数字序列可能为 [3，7]，或 [4，8]，或[5，9]，第一行必然出现的候选数为{5，6，7}，即 L(A1)= {5，6，7}。

2.3 单元格候选数的确定

若某个单元格所在行、正斜线、反斜线得到的候选数范围为 [m1，M1]，[m2，M2]，[m3，M3]，则该单元格的初始候选数为[d，u]，其中 d=max{m1，m2，m3}，u=min{M1，M2，M3}。

如图1，单元格 (1，1)的三维向量为 (1，1，5)，它所在第一行中 a=6，b=7，L=5，则第一行候选数范围为[3，9]；它所在第一条正斜线中 a=3，b=6，L=5，则第一条正斜线候选数范围为[2，7]；它所在第五条反斜线中a=2，b=8，L=9，则第五条反斜线候选数范围为 [1，9]；那么单元格 (1，1)的初始候选数为3，4，5，6，7。

2.4 建立决策变量

为表达方便，设所有解未确定的变量都取xijk=-1，表示数字k为格子(i，j)的候选数。

3 线性规划方程组的性质

3.1 候选数删除性质

性质3.1.1若 xijk=1，则 xijl=0，l≠k 。当格子 (i，j)的数字确定时，利用该性质可删除该格子上的其余候选数。

性质 3.1.2若 xijk=1，则 xilk=0，(i，j)∈ At，(i，l)∈ At，l≠j，t=1，2，…，9 。当格子 (i，j)的数字确定为 k 时，利用该性质可删除该格子所在第t行区其他格子上的候选数k。

性质 3.1.3若 xijk=1，则 xmnk=0，(i，j)∈ Bt，(m，n)∈Bt，(i，j)≠(m，n)，t=1，2，…，9 。当格子 (i，j)的数字确定为k时，利用该性质可删除该格子所在第t正斜线区其他格子上的候选数k。

性质 3.1.4若 xijk=1，则 xmnk=0，(i，j)∈ Ct，(m，n)∈Ct，(i，j)≠(m，n)，t=1，2，…，9 。当格子 (i，j)的数字确定为k时，利用该性质可删除该格子所在第t反斜线区其他格子上的候选数k。

3.2 确定性性质

为表示方便，建立函数：

性质3.2.2若 xijk=-1，k∈[M+1-L，m-1+L]对任意的 (m，n)∈ At，(i，j)∈ At，(i，j)≠(m，n)，都有 xmnk≠ -1，则必有xijk=1。该性质表示当该格子在第t行区存在必定出现的数字，并且第t行区的其他格子未存在时，该格子所填数字必为候选数k。

性质3.2.3若 xijk=-1，k∈[M+1-L，m-1+L]对任意的 (m，n)∈Bt，(i，j)∈Bt，(i，j)≠(m，n)，都有 xmnk≠-1，则必有xijk=1。该性质表示当该格子在第t正斜线区存在必定出现的数字，并且第t正斜线区的其他格子未存在时，该格子所填数字必为候选数k。

性质3.2.4若 xijk=-1，k∈[M+1-L，m-1+L]对任意的 (m，n)∈ Ct，(i，j)∈ Ct，(i，j)≠(m，n)，都有 xmnk≠ -1，则必有xijk=1。该性质表示当该格子在第t反斜线区存在必定出现的数字，并且第t反斜线区的其他格子未存在时，该格子所填数字必为候选数k。

3.3 矛盾性质

性质3.3.1若对某固定格子(i，j)，对任意数字k，都有 xijk=0或1。若则导致该数独矛盾。该性质表明任何一个格子所填的数只能有1个。

性质3.3.2若对某固定区t及数字k，对任意格子(i，j)∈At都有xijk=0 或 1。若2，…，9)，则导致该数独矛盾。该性质表明任何一个数在任何一个行区只能填1次。

性质3.3.3若对某固定区t及数字k，对任意格子(i，j)∈Bt，都有xijk=0 或 1。若2，…，9)，则导致该数独矛盾。该性质表明任何一个数在任何一个正斜线区只能填1次。

性质3.3.4若对某固定区t及数字k，对任意格子(i，j)∈Ct，都有xijk=0 或 1。若2，…，9)，则导致该数独矛盾。该性质表明任何一个数在任何一个反斜线区只能填1次。

3.4 不变性

性质 3.4.1对某固定格子 (i，j)，若 xijk=-1，k∈{m，m+1，…，M}，即格子 (i，j)候选数为 m，m+1，…，M 。对所有候选数k，当 xijk=1时，某个格子(p，q)都不能填r，则xpqr=0。对某个候选数k，当xijk=1时导致数独矛盾，则必有xijk=0。

性质 3.4.2对某 r(r=2，3，4，…)个固定格子 (i1，j1)，(i2，j2)，…，(ir，jr)，若 xi1j1k1=-1，k1∈{m1，m1+1，…，M1}，…，xirjrkr=-1，kr∈{mr，mr+1，…，Mr} 。即格子 (i1，j1)的候选 数为 m1，m1+1，…，M1，格子 (ir，jr) 的候选数为 mr，mr+1，…，Mr。当对r个格子的多有候选数来说，当xi1j1k1=-1，…，xirjrkr=-1时，某个格子 (i，j)都不能填 r，则xijr=0。

4 算法应用及实例计算

综合前面由线性规划方程组得到的四类性质，本文提出求解该方程组的算法。

初始化：将数独谜题存放在数组T[9][9]中，若格子(i，j)为空格，则令 T[i][j]=0 ；若格子 (i，j)已填入数字k，则令T[i][j]=k。基于蜂巢数独独特的形状，为了保证数组的完整性，其他未有格子的部分填-1。将数独格子的候选数存放在数组x[9][9][9]中，同样地，若格子(i，j)为空格，则令 x[i][j][k]=-1，k=1，2，…，9 ；若格子(i，j)已填入数字 k，则令 x[i][j][k]=1，x[i][j][l]=0(l≠k)。

步骤1根据2.3节的方法确定每个格子的候选数，然后根据3.1节性质进行候选数的删除。

步骤2根据3.2节性质确定性对数独进行填写，若完整则程序结束，否则进入下一步。

步骤3对格子进行单区枚举，删除每个区中各格子的候选数。对任意一个区进行满足连续序列的枚举。将引起矛盾的候选数组合删除，记录没有引起矛盾的候选数组合及由前面推理得到的新的候选数表，将得到的所有候选数表求并，从而得到各空格新的候选数集。实现删除候选数的目标。

步骤4利用每个区各格子新的候选数集，删除其他相关格子中的候选数。

步骤5若数独未填写完整，转入步骤3，若填写完整，程序结束，输出结果。

步骤6对格子进行两区枚举，删除两个区中各格子的候选数。对任意两个区进行满足连续序列的枚举，然后进行同步骤3相同的处理。

步骤7若数独未填写完整，转入步骤4，若填写完整，程序结束，输出结果。

对图1利用候选数删除和确定操作之后，空格减少了6个，如图2所示。再进行一次单区枚举后，数独已经完成，如图3所示。

图2 确定性操作结果

图3 单区枚举结果

再如，对图4所示的中级谜题，进行文献[11，15]中的空格枚举算法同本文提出的区域序列枚举法对比实验。结果显示，空格枚举算法中，当枚举空格数增大到4的时候，还是无法求解出此谜题。然而当采用本文提出的区域序列枚举算法时，谜题结果如图5所示。进行确定及空格枚举操作后，空格数同样也并未减少，选取第9行区进行枚举，符合的连续序列有：34567和45678，将这两组序列进行已知数4和7的排列组合，符合它的序列有12种，如：37546，37645等等。经过单区序列枚举得到结果图5所示。

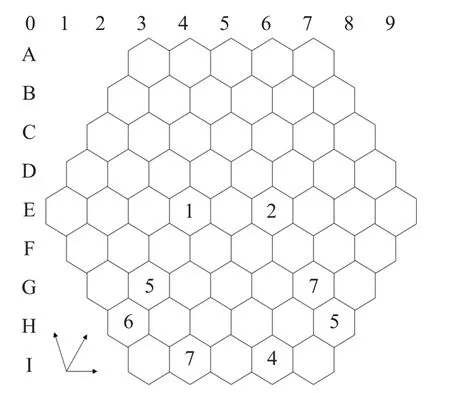
图4 中级蜂巢数独谜题

图5 中级蜂巢区序列枚举结果

经过同文献[11]中提出的算法进行对比实验，得出少量的初级蜂巢数独谜题只需空格枚举就可以完成，对于中级甚至高级谜题，单空格枚举和多空格枚举失效，但是采用序列的区域枚举就可以完成。这就体现出了蜂巢数独其独特的规则，即序列的连续性。这是它和标准数独在算法上面的不同点。

5 结论

本文提出的对蜂巢数独问题的方程组求解算法，利用了数独问题对应的方程的性质进行候选数的删除和更新，实现了由空格枚举[11，15]向序列枚举的转变。对绝大多数的数独问题，用很少格子的枚举就能实现求解，而且计算时间都在毫秒级。但是这种空格枚举的方法只能针对初级及极少数中级的蜂巢数独谜题，当空格数少于8个甚至更少的时候，这种空格枚举方法的作用就很小了，于是区序列枚举算法就起到了至关重要的作用。但是本文提出的算法即使再使用多区序列枚举后，高级蜂巢数独谜题的实现效率依然很低，同时当蜂巢数独需要经过同时枚举几个区才能获得时速度比较慢，可以考虑改进的方法。这将是下一步将要做的工作。

[1]Garns H.Number place[J].Dell Pencil Puzzles&Word Games，1979，16（5）.

[2]Bartlett A，Chartier T P，Langville A N，et al.An integer programming modelforthesudoku problem[EB/OL].（2006-03-10）.http：//www.cofc.edu/langvillea/Sudoku/sudoku2.pdf.

[3]Simons F.Solving a sudoku puzzle with mathematica[J]. Mathematica in Education and Research，2005，10（4）：1-24.

[4]肖华勇，田铮，马雷.数独基于规则的逐步枚举算法设计[J].计算机工程与设计，2010，31（5）：1035-1037.

[5]Posthoff C，Steinbach B.Sudoku solutions using logic equations[Z].2008.

[6]刘延风，刘三阳.基于遗传算法求解数独难题[J].计算机科学，2010（3）：225-226.

[7]Khan S，Jabbar S，Jabbari S，et al.Solving sudoku using probabilistic graphical models[Z].2009.

[8]Goldberger J.Solving sudoku using combined message passing algorithms[Z].[S.l.]：School of Engineering，Bar-llan University，2007.

[9]Lynee I，Ouaknin J.Sudoku as a SAT problem[C]//Proc of the 9th International Symposium on Artificial Intelligence and Mathematics，2006.

[10]Bondy J A，Murty U S R.Graph theory with applications[M].London：Macmilian，1976.

[11]肖华勇，程海礁，王月兴.九宫数独的方程求解算法研究[J].计算机应用，2012，32（10）：2907-2910.

[12]Lewis R.Metaheuristics can solve sudoku puzzles[J].Journal of Heuristics，2007，13：387-401.

[13]直观法玩数独——SUDOKU[EB/OL].[2012-10-20].http：// hi.baidu.com/kiwy07/item/2e00ad1665e41458f0090e0b.

[14]Lei Lei，Shen Fuke.The design and implementation of the algorithm about sudoku[J].Computer Knowledge and Technology，2007，2：481-482.

[15]肖华勇，马丽娜，程海礁.老板数独的方程求解算法研究[J].计算机工程与应用，2014，50（9）：41-44.

XIAO Huayong,YANG Feifei,HUANG Benru

Department of Mathematics,School of Science,Northwestern Polytechnical University,Xi’an 710129,China

Honeycomb sudoku is a kind of deformation of sudoku which is similar to the honeycomb and difficult to solve.Section 1 of the full paper presents the linear programming equation set equivalent with the honeycomb sudoku puzzle. Section 2,the properties of the solution algorithm of honeycomb sudoku are derived from the equation set,such as the property of removing the candidate numbers,the contradictoriness,the unique certainty and the invariance of enumeration.Section 3 solves the honeycomb sudoku with a regional sequence enumeration method,and the difference of solving algorithm between the honeycomb sudoku and standard sudoku is compared.The proposed algorithm is proved effective for the honeycomb sudoku of medium level by examples.

honeycomb sudoku;deformation of sudoku;equation set;regional sequence enumeration method

蜂巢数独是类似蜂巢难度又高的变形数独，它有着重要的研究意义。由蜂巢数独谜题提出与之等价的线性规划方程组；从方程组出发推导出求解数独算法的性质，如候选数删除性质、矛盾性质、唯一确定性质、枚举不变性质；基于以上性质，提出用区域序列枚举方法求解蜂巢数独。结合实例计算，提出的算法对中度难度级别的蜂巢数独是有效的。

蜂巢数独；变形数独；方程组；区域序列枚举

A

O157

10.3778/j.issn.1002-8331.1305-0513

XIAO Huayong,YANG Feifei,HUANG Benru.Equation model for honeycomb sudoku based on regional sequence enumeration method.Computer Engineering and Applications,2014,50（23）：36-40.

西北工业大学2013大学生创新项目基金（No.07gz1601）。

肖华勇（1969—），男，博士，副教授，主要研究方向：统计优化；杨菲菲（1988—），女，硕士研究生，主要研究方向：统计优化；黄奔茹（1992—），女，主要研究方向：统计学。E-mail：yangfeifei@mail.nwpu.edu.cn

2013-06-04

2013-07-22

1002-8331（2014）23-0036-05

CNKI网络优先出版：2013-08-15,http://www.cnki.net/kcms/detail/11.2127.TP.20130815.1635.003.html