UO2不同表面的磁结构和稳定性研究

刘 兵, 戴振宏, 王 森, 徐 雷

(烟台大学光电信息科学技术学院,山东 烟台 264005)

UO2是一种目前广泛应用的陶瓷核燃料,近几年在实验上和理论上都对其结构、导电性、磁学和光学等性质做了广泛的研究[1-8].实验上光学性质的分析证实,块体材料UO2为绝缘体,带隙约为2.1 eV[1].

铀元素属于锕系金属,存在强局域性和强关联性的f壳层电子,导致其氧化物UO2中晶体为强关联体系,使得原本为不满填充的导带发生了能带分裂,产生带隙,发生了导体向绝缘体的转变,即UO2为一种Hubbard-Mott绝缘体.又由于其f壳层是未满填充的能带,所以UO2是一种反铁磁体系[3].因此传统的密度泛函理论计算[9]无法准确预测其带隙宽度.近年来,越来越多的研究者采用不同的理论方法,即LSDA+U[10]、杂化泛函[2]的方法得到了正确的结果,证实了它的绝缘体性质.

UO2晶体结构为萤石结构,如图1所示.UO2作为核燃料,处在核反应堆中的高温高压下,其内部存在大量的缺陷,晶体可能会沿不同的晶面发生解离,形成表面结构.因此,对表面的研究有助于理解晶体的解离行为与晶体内部的晶界缺陷结构,并能对实验起到指导和参考的作用.本文应用vasp软件[11],使用LSDA+U[12]方法,对不同表面的表面能、结构、电荷分布和磁矩性质等做了研究.

图1 萤石结构的UO2

对于体材料磁性的研究, 大多数人的研究结果[1-6,8]表明反铁磁态为基态,而Skomurski F N等[7]的研究结果表明铁磁性为基态.本文对反铁磁态和铁磁态都进行了计算,铁磁比反铁磁在能量上低约0.04 eV,而这与Skomurski F N等的结果(0.03 eV)相同.

对于表面能的研究,定性上是一致的,都是(111)面能量最低,但在定量上,不同的研究者[6-8]得到的结果不同. Skomurski F N等得到的铁磁态结果为0.46 eV,而本文的结果为0.73 eV.反铁磁状态下,Evarestov R等[8]的结果为0.94 eV,而本文为0.35 eV.这种不一致性是由使用的计算方法不同造成的,Evarestov R等使用的是杂化泛函的方法,而本文采用密度泛函理论(DFT),但3种表面的相对的形成能是不变的,都是(111)面形成能最低.

1 计算方法

以晶格常数的实验值0.547 0 nm[13]为初始结构开始优化.为了简便,取沿z方向的1k反铁磁,分别进行全弛豫和固定原胞形状弛豫.全弛豫的结果为a=b=0.555 8 nm,c=0.549 5 nm,固定原胞弛豫的结果为a=b=c=0.553 1 nm.前者比后者更加稳定,稳定性在能量上低约0.004 eV,差别非常小.而对后者结构的铁磁性计算,结果显示铁磁性比反铁磁性能量低约0.04 eV.为了保持构造出的表面结构不同晶面族的晶面间距相等,以固定原胞弛豫的结果构建(111)、(110)和(100) 3种表面.它们都为层状结构,为了尽可能地减少层间的相互作用,真空层厚度都在1 nm以上.

计算使用的软件为vasp软件包[11],所有的计算采用投影缀加波方法(PAW),交换关联项采用广义梯度近似的方法(PBE-GGA)来处理.由于UO2是一种强关联体系,需要加入Hubbard U修正,U值和J值分别为4.50 eV和0.51 eV[14],使用Dudarev机制[12],所以只有它们的差值才起作用.将U原子的6s26p66d15f37s2和O原子的2s22p4作为价电子处理.

计算中波函数采用实空间投影,平面波的截断能取450 eV,电子自洽计算的能量收敛精度取为1.0×10-5eV.离子弛豫采用的力收敛标准为0.1 eV/nm.对于完整晶格,倒空间网格采用Monkhorst-Pack自动生成机制[15],最小取为4×4×4,对于表面,倒空间网格选取为4×4×1.倒空间中积分的分布函数采用高斯分布函数,展宽为0.1 eV.

实验结果表明UO2为3k反铁磁体系[16],但为了简化和与完整晶体的UO2作对比,计算中反铁磁的计算采用沿z方向的1k反铁磁.计算采用slab模型,固定原胞大小,进行选择性弛豫.3种表面的结构分别如图2所示,从左至右依次为(111),(110)和(100)面. (111)面的原胞结构为0.782 nm×0.782 nm×2.5 nm,a和b方向的夹角为60°.a和b均垂直于c方向.每个原胞有12个U原子,24个O原子,共有9层原子,离子弛豫时保持最下面3层不动,上面6层都动. (110)面的原胞结构为0.782 nm×0.553 nm×2.5 nm,a、b和c方向相互垂直.每个原胞有12个U原子和24个O原子,共有6层,离子弛豫时保持最下面3层不动,上面3层可动. (100)面的原胞结构为0.553 nm×0.553 nm×2.5 nm,a、b和c方向相互垂直.每个原胞有8个U原子和16个O原子.共有8层,离子弛豫时,保持最下面3层不动,上面5层可动.铁磁态的计算与反铁磁态的计算采用完全相同的晶格结构.

图2 UO2的3种表面侧视图

Bader电荷分析[17]是采用Bader的方法来处理电荷分布,以电荷密度梯度为零的地方为分界线,将电荷进行归置.

对于表面能量计算,首先定义弛豫能,弛豫能为弛豫后与弛豫前的能量差为

σrelax=Erelax-Eunrelax,

弛豫前的表面能为

最后得到总表面能为

其中:S是原胞在底面上的投影面积,Natom是原胞中UO2的数目,Ebulk为体材料的UO2内能.

表面浓度的计算采用波尔兹曼分布,定义表面面积相对浓度:

其中:i代表3种不同的表面.

2 结果和讨论

先采用相对较高的精度ENCUT=550 eV和6×6×6的K点网格,加入反铁磁保持原胞形状不变计算得到平衡的晶格结构为a=b=c=0.553 1 nm,实验值为0.547 0 nm[13].磁矩为2.0 μB,与实验值(1.7～1.8)[3]符合的较好.从态密度图(图3)得到的带隙宽度为2.06 eV,也与实验值(2.1 eV)[1]符合的很好.

图3 反铁磁UO2晶体的态密度

铁磁的计算结果显示铁磁态比反铁磁态更稳定,能量要低0.04 eV左右,这与Skomurski F N等的结果(0.03 eV)相似.磁矩为2.0 μB.铁磁态的带隙为2.09 eV.

2.1 截断能与倒空间K网格的测试

对截断能与倒空间网格的测试结果如图4所示,当精度足够大时,2种测试结果都会收敛到大约-116.4 eV.图4(a)为截断能的测试结果,当截断能取450 eV以及更大,能量的变化不会大于0.1 eV.这表明,要想得到较为精确的结果,截断能至少要取450 eV,而我们在以下的计算中均取为450 eV.图4(b)为K点网格的测试结果,分别对2种K点生成机制(Monkhorst-Pack机制和Gamma机制)做了测试.当K网格取3×3×3以及更大,能量变化不会大于0.001 eV,因此K点网格不管选用何种生成机制,选用3×3×3以及更高密度的K点均能达到收敛的能量.我们在以下的计算中均取为Monkhorst-Pack机制的4×4×4精度以上的网格.

图4 截断能与倒空间网格的测试结果

2.2 表面能

3种表面的表面能如表1所示,表面能的单位为J·m-2.磁序不同,则原子间相互作用不同,表1中,AFM与FM的结果并不完全一致.但是,不论是反铁磁态还是铁磁态,(111)面的形成能都是最低的,因此(111)面是最稳定的,而最不稳定的是(100)面.其原因是,(100)面的U面和O面晶面间距较大,因此在结构弛豫时,(100)表面的原子位移较大,引起能量的较大改变.文献[6]以铁磁态为基态,本文的计算结果的趋势与参考文献[6]相同,而数值的不同在于文献[6]使用的是全弛豫的slab模型,而本文采用选择性弛豫的slab模型.

Evarestov R等[8]以反铁磁态为基态,计算的(111)面的结果为0.94 eV,比本文的计算结果大2倍左右.其原因是Evarestov R等使用的是杂化泛函方法,而本文采用密度泛函方法,方法不同所致.但是相对趋势是一致的,都是(111)面形成能最低.

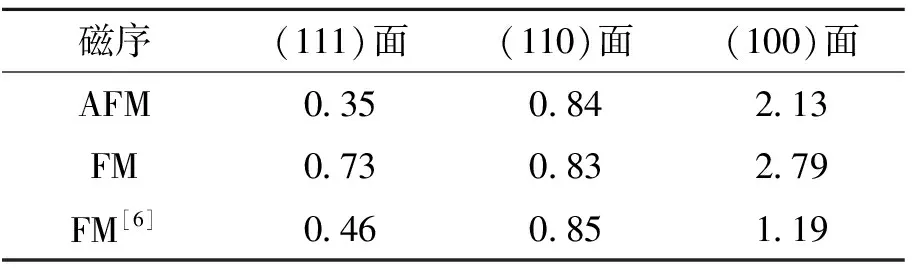
表1 表面能

2.3 结构、Bader电荷与磁矩分析

表2和表3分别给出了反铁磁和铁磁状态下离子弛豫之后表面原子的位置变化、Bader电荷分析和磁矩情况,其中位置一栏中元素的下标s和ss分别表示表面原子和次表面原子.位移一栏正值表示弛豫之后向外膨胀,负值表示收缩.键长RU—O一栏表示表面处的RU—O与体材料的对比.

Bader电荷一栏中,正数表示得到电子,负数表示失去电子.磁矩中的正负号只表示磁序,与大小无关.其中黑体部分表示变化非常明显的数据.

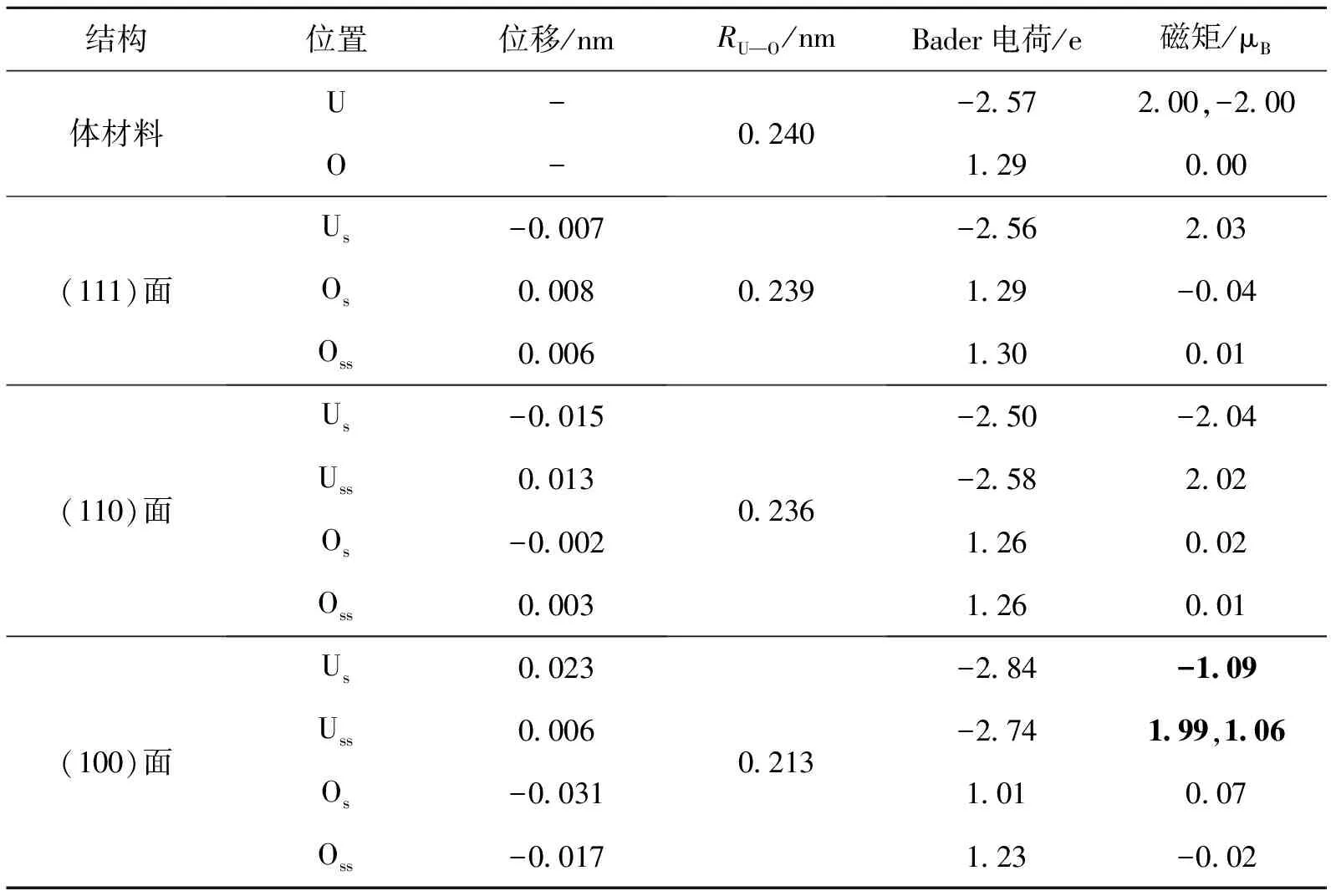
表2 反铁磁态下的计算结果

表3 铁磁态下的计算结果

2.3.1 反铁磁态 首先分析反铁磁情形,由表2可知,(111)表面的O-U-O面整体向内收缩,表面U原子层向内收缩了约0.007 nm,位移不明显.(110)面最外层既有O原子,又有U原子,表面原子向内收缩,次表面原子向外膨胀,U原子的位移要比O原子更明显.(100)面最外层为O原子,且有比较明显的收缩,而表面的U原子向外膨胀,导致U-O键长变短,次外层的U原子和O原子也有相似的微小的位移.3种表面的RU—O都变短了,而只有(100)面的键长变化是明显的.

原子位置的变化造成了电荷的重新分布.由Bader电荷分析可知,体材料中的U原子并不是严格的丢失4个电子变成+4价的阳离子,而是与O原子形成了共价键,每个U原子平均失去2.57个电子,每个O原子平均得到1.29个电子.形成(111)表面和(110)表面以后,电子的分布并没有很大改变.而形成(100)面以后,虽然表面RU—O变短,但是表面和次表面O原子距离变小,电子相互排斥,所以这2层的O原子所得电子数变小,而U原子失去的电子数变多.晶体内部,如第三层第四层O原子间距离基本不发生变化,多余的电子转移到这几层中.

(100)面这种重新分布同时也造成了磁矩的较大的变化,并且次表面的U原子磁矩变的不对称如表2中的黑体数字所示.U原子中的磁性来源于局域轨道d、f电子,与体材料相比,表面U原子有更多的局域d、f电子转移到O原子中,则这些U原子的磁矩要变小,而表面O原子磁矩略微变大.而(111)和(110)表面原子位移较小,因此它们的磁矩变化不大.

2.3.2 铁磁态 表3给出了铁磁状态下结构、电荷分布和磁矩情况.铁磁态的结果与反铁磁状态相似.

(111)面U原子向内收缩,与反铁磁态相同.而O原子向外膨胀.(110)面和(100)面与反铁磁态位移趋势基本相同.RU—O与反铁磁态也几乎相同.

由于结构变化的相似性,铁磁态的Bader电荷分布与反铁磁态几乎完全相同,而磁矩的大小也相似.相似的结构变化导致了相似的电荷分布和磁性结构.

2.4 3种表面的相对浓度

由块体材料形成表面的过程可以看作是晶体解离的过程,所以表面的浓度可以看作是解离面的浓度.我们根据上面得到的表面能,结合玻尔兹曼统计分布,计算了反铁磁态下3种表面相对浓度随温度的变化,如图5所示.铁磁态的相对浓度变化趋势与反铁磁态相同.

图5给出了最高到1 600 K温度下UO2不同表面的浓度.实方框代表(111)面,空心圆代表(110)面,空心三角形代表(100)面.由于(111)面的表面能最低,所以其浓度也最高.其次为(110)面,(100)面的浓度最低.在温度从0到1 600 K的变化过程中,(111)面的相对浓度始终是最大的.

图5 反铁磁状态下不同表面的相对浓度

3 结 论

我们通过LSDA+U方法,测试了截断能和倒空间K网格,正确计算了块体UO2的带隙和结构,并把该方法用于计算UO2反铁磁和铁磁状态下的3种表面. 表面能计算结果显示,不论是反铁磁态还是铁磁态,(111)面都是最容易形成的,而 (100)面最不稳定.

2种磁性状态的计算结果在结构、Bader电荷分布和磁矩上非常相似.由于(100)表面在弛豫时结构有较大的变化,表面和次表面U、O原子的Bader电荷布居数变小,并且表面与次表面U原子的磁矩变小,而表面O原子磁矩略微变大.最后,计算了不同解离面的相对浓度大小在0到1 600 K温度范围内的变化,(111)面的相对浓度是最高的.因此可以预测在核燃料UO2的多晶结构中,晶界大部分是以(111)面出现的.

参考文献:

[1]Schoenes J. Optical properties and electronic structure of UO2[J]. Journal of Applied Physics,1978,49(3):1463-1465.

[2]Kudin K N, Scuseria G E, Martin R L. Hybrid density-functional theory and the insulating gap of UO2[J]. Physical Review Letters,2002,89(26):266402(4).

[3]Fraxer B C, Shirane G, Cox D E, et al. Neutron-diffraction study of antiferromagnetism in UO2[J]. Physical Review,1965,140(4A):A1448-A1452.

[4]陈秋云,赖新春,王小英,等.UO2的电子结构及光学性质的第一性原理研究[J].物理学报, 2010,59(7):4945-4949.

[5]Geng Huayun, Chen Ying, Kaneta Y, et al. Point defects and clustering in uranium dioxide by LSDA+U calculations [J]. Physical Review B,2008,77,104120(16).

[6]Skomurski F N, Ewing R C, Rohl A L, et al. Quantum mechanical vs. empirical potential modeling of uranium dioxide (UO2) surfaces: (111), (110), and (100) [J]. American Mineralogist,2006,91:1761-1772.

[7]Boyarchenkov A S, Potashnikov S I, Nekrasov K A, et al. Molecular dynamics simulation of UO2nanocrystals surface [J]. Journal of Nuclear Materials,2012,421:1-8.

[8]Evarestov R, Bandura A, Blokhin E. Surface modelling on heavy atom crystalline compounds: HfO2and UO2fluorite structures [J]. Acta Materialia,2009,57:600-606.

[9]Kohn W, Sham L J. Self-Consistent equations including exchange and correlation effects [J]. Physical Review,1965,140(4A):A1133-A1138.

[10]Anisimov V I, Zaanen J, Andersen O K. Band theory and mott insulators-hubbard U instead of stoner I [J]. Physical Review B,1991,44(3):943-954.

[11]Kresse G, Furthmullerprb J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Physical Review B,1996,54(16):11169-11186.

[12]Dudarev S L, Botton G A, Savrasov S Y, et al. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study [J]. Physical Review B,1998,57(3):1505-1509.

[13]McEachern R J, Taylor P. A review of the oxidation of uranium dioxide at temperatures below 400°C [J]. Journal of Nuclear Materials,1998,254:87-121.

[14]Geng Huayun, Chen Ying, Kaneta Y, et al. Structural behavior of uranium dioxide under pressure by LSDA+U calculations [J]. Physical Review B,2007,75,054111(8).

[15]Monkhorst H J, Pack J D. Special points for Brillonin-zone integrations [J]. Physical Review B,1976,13(12):5188-5192.

[16]Wilkins S B, Caciuffo R, Detlefs C, et al. Direct observation of electric-quadrupolar order in UO2[J]. Physical Review B,2006,73,060406(4).

[17]Sanville E, Kenny S D, Smith R, et al. Improved grid-based algorithm for Bader charge allocation [J]. Journal of Computational Chemistry,2007,28(5):899-908.