关于ω-稠密度的一个注记

杨 洁

(聊城大学东昌学院, 山东 聊城 252000)

1 预备知识

陈水利[1]引入了一种具有广泛意义的L-fuzzy保序算子空间,简记为L-保序算子空间,并给出ω-闭集,ω-基,ω-子基等概念．文献[2-4]中将一些常见的算子进行统一,建立了L-保序算子空间的基本理论．文献[5-6]继续在L-保序算子空间中引入基本的基数函数:ω-权,ω-特征和ω-稠密度并系统地讨论了这些概念的基本性质及关系．

在文献[6]的最后,作者提出了一个问题:点集拓扑学中关于浓度成立的Hewitt-Marczewski-Pondiczery定理是否关于ω-稠密度能够成立?

本文将研究上述问题并给出一个部分解答．L为fuzzy格,M是L中所有分子的集合．LX表示在非空集合X上定义,在L中取值的所有L-fuzzy集合构成的集族．1X和0X分别指LX中的最大最小元．LX中的所有分子的集合记为M*(LX)．基数ω0是指最小无限基数．本文中的基数m≥ω0,其它相关概念和符号可参考文献[1,5-6]．

定义1[1]设X是一个非空集合,ω:LX→LX是满足下列条件的算子:(i)ω(1X)=1X,(ii) ∀A,B∈LX,A≤B⟹ω(A)≤ω(B), (iii) ∀A∈LX,A≤ω(A)．则定义ω为一个L-fuzzy保序算子．若A=ω(A),称A为LX的一个ω-集,记Ω={A∈LX:A=ω(A)}．称(LX,Ω)是L-fuzzy保序算子空间,记为L-保序算子空间．

定义2[6]设(LX,Ω)为L-保序算子空间,xα∈M*(LX),P∈LX．若存在Q∈Ω,使xα>Q并且P≤Q,则称P为xα的一个ω-远域．xα的所有ω-远域组成的集族记作ωη(xα)．若A∈LX且∀P∈ωη(xα)有A>P,则称xα为A的ω-附着点． 定义A的所有ω-附着点之并为A的ω-闭包,记为ωcl(A)．若ωcl(A)=A, 则称A是LX中的ω-闭集． (LX,Ω)中所有的ω-闭集构成的集族记作ωC(A)．若A为ω-闭集,称A′为LX中的ω-开集．

2 L-保序算子空间的ω-稠密度

L-保序算子空间中ω-稠密度的概念如下:

定义3[6]设(LX,Ω)是L-保序算子空间,A∈LX． 定义LF集A的势|A|=min{|φ|:φ⊆M*(LX),∨φ=A}．d(LX,Ω)=ω0+min{|A|:A∈LX,ωcl(A)=1X}记为(LX,Ω)的ω-稠密度．

注:ω为L-fuzzy闭包算子时, 上面的定义即指文献[7]中的稠密度．

在点集拓扑学中,Hewitt-Marczewski-Pondiczery定理如下:

定理1[8]如果∀t∈T,d(Xt)≤m,且|T|≤2m,则有d(∏t∈TXt)≤m．

研究证明HPV的感染是可以预防的，并且宫颈癌可能成为第一个可以用疫苗预防的癌症。研究发现，HPV的L1蛋白保守度高，因此可以作为HPV的特异性抗原用来研究制造病毒预防疫苗。目前市面上的预防疫苗都是利用重组的DNA分子所表达的病毒样颗粒(virus-like particles， VLPs)制成的疫苗。

经过研究发现,在L-保序算子空间中加上一个相关条件后,关于ω-稠密度的Hewitt-Marczewski-Pondiczery定理是可以成立的,即:

定理2 设{(LXt,Ωt)}t∈T是一族L-保序算子空间,(LX,Ω)是其积空间．如果(i)∀t∈T,d(LXt,Ωt)≤m,(ii)|T|≤2m,且(iii)L中有分子集φ,满足∨φ=1L,|φ|≤m且φ为定向集合,则d(LX,Ω)≤m．

证明取集合Γ满足|Γ|=m．对于∀α∈Γ,设Tα是由两个点组成的离散拓扑空间．设S=∏α∈ΤTα,则有|S|=2m．又因为Tα上的拓扑为离散的,故其乘积空间(S,φ)满足T2分离公理．设S是φ中全部乘积形状的非空开集,则有|S|=m．设R是S中的有限多个两两不相交的非空开集组成的各种子族的全体,则|R|=m．由条件(ii),不妨设T为S的子集．

设∀t∈T,d(LXt,Ωt)≤m．取At⊂ LXt, 使得ωclXt(At)=1Xt,并且| At|≤m. 设Yt=suppAt,则有| Yt|≤m. 取集合Z,满足| Z|=m.则∀ t ∈ T, 存在满射ft:Z→Yt．

对于∀r∈R,我们将在X=Πt∈TXt中做出不超过m个点,这样与R中全体r相对应,一共做出不超过m*m=m个点．然后以这m个点为承点,构造分子xλ,其高度λ取值于φ,则这种分子的个数仍然不超过m．我们证明它们并的ω-闭包等于1X,则证明完成．

∀r={U1,…,UK}∈R,这里U1,…,UK是S中两两不相交的非空开集,做点x={xt}t∈T∈X如下:

其中：z1,…, zk+1是Z中任取的点．

又因为| Z|=m.所以对于某一固定的∀r∈R,按此过程可以得到X中不超过m个点,其全体记作E(r),则| E(r) |≤m．令E=∪r∈RE(r)⟹| E |≤m．令ψ={xλ:x∈E,λ∈φ},则有| ψ |≤m,设A=∨ψ,下证ωcl(A)=1X．

(1)

因为(S,φ)满足T2分离公理,t1,…,tk是T中从而也是S中两两不同的点．所以有

S中存在两两互不相交的开集U1,…,UK满足ti∈Ui(i=1,…,k).

这时有r={U1,…,UK}∈R．并且对于∀i≤k, 由于fti:Z→Yti为满射,可以取Zti∈Z满足f(Zti)=yti,再任取一点z∈Z,令x={xt}t∈T∈X满足:

则由x ∈E且xti=f(Zti)=yti可知xλ∈ψ．

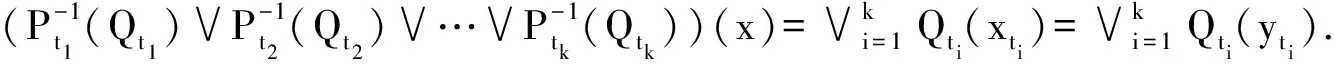
注意到上述条件(iii)与条件“1L是L中的并既约元”是等价的,则经过类似的证明可以得到定理3.

定理3 设{(LXt,Ωt)}t∈T是一族L-保序算子空间,(LX,Ω)是其积空间．如果(i)∀t∈T,d(LXt,Ωt)≤m,(ii)|T|≤2m,且(iii)1L是L中的并既约元,则d(LX,Ω)≤m．

参考文献:

[1]ChenShuili.OnL-fuzzyorder-preservingoperatorω-spaces[J].TheJournalofFuzzyMathematics, 2006,14(2):481-499.

[2]陈水利,董长清.L-fuzzy保序算子空间中的连续[J].模糊系统与数学,2002,16(3): 36-41.

[3]HuangZhaoxia,ChenShuili.ωθ-countabilityinanLω-space[J].AdvancesinIntelligentandSoftComputing,2010,82: 519-526.

[4]黄金兰,陈水利.Lω-空间中ω-tychonoff的分离性[J].模糊系统与数学,2012,26(4):43-48.

[5]杨洁.可拓扑生成的L-fuzzy保序算子空间的权，特征及稠密度[J].模糊系统与数学,2014,28(1):53-56.

[6]陈斌.L-fuzzy保序算子空间的基数函数[J].山东大学学报:理学版,2007, 42(12): 119-122.

[7]王国俊.L-fuzzy拓扑空间论[M].西安:陕西师范大学出版社,1988.

[8]EngelkingR.GeneralTopology[M].Warszawa:PWN-PolishScientificPublishers, 1977.