考虑轴压比的圆钢管抗冲击有限元研究
刘富强,曲 慧,周新刚,黄文金
(1.烟台大学土木工程学院,山东 烟台 264005;2. 福建农林大学交通与土木工程学院, 福建 福州350002)
文献[1]在实验的基础上,提出圆钢管在受撞击时钢管共呈现出3种不同的变形情况:局部凹陷、整体弯曲以及两者之间的耦合.张善元课题组等[2-5]从1996年到现在进行了大量钢管冲击力学性能的实验和有限元研究,在对两端固支圆管的冲击试验后,得出了钢管的整体变形与局部凹陷的耦合程度与钢管的几何参数L/D,D/t有很大关系的结论.文献[6]在做钢管混凝土的侧向冲击下的动力响应及损伤破坏的研究时,对空钢管构件也做了相关冲击试验.对无轴向压力钢管在不同冲击高度的实验研究中指出钢管的变形首先是发生局部凹陷,当冲击能量逐渐增大,使钢管截面凹陷到一定程度时才发生整体弯曲变形.
在实际工程中,钢管结构大多受轴压力作用,例如:高速公路收费站立柱受到屋盖上荷载的轴向压力;海洋平台圆钢管柱受到自重及其他偶然荷载的轴压力作用.所以钢管受到撞击时,研究轴向压力对其受冲击性能的影响就显得很有必要.文献[7-10]在从事海洋平台损伤研究时,进行带轴力钢管的准静态横向荷载的实验研究和有限元分析,提出轴向压力对钢管所受横向冲击力和冲击能量有较大影响,研究了不同边界条件和几何参数对变形的影响.通过有限元软件ABAQUS对试验进行了模拟,将得到的试验数据与有限元模拟进行比较,两者结果基本吻合.证明了管结构的冲击力学性能用有限元软件模拟和预测很合理.进一步指出轴向力对受横向冲击的管结构的变形、承载力影响较大.
本文对一端固支一端施加轴压比分别为0,0.25和0.5轴压力的薄壁圆管在经受楔形锤体冲击时的力学性能进行了有限元研究,得到圆钢管在不同轴压力作用下经受侧向冲击后对构件破坏模态、承载力、变形和能量等冲击性能的影响.
1 有限元模型
1.1 有限元模型的建立
本文采用有限元分析软件ABAQUS进行冲击性能模拟,建立的模型分两部分:楔形锤体和薄壁圆管试件.采用ABAQUS三维实体建模,分析过程中,采用三维八结点实体单元(C3D8R).构件信息如表1所示.冲击示意图如图1.

表1 构件信息表

图1 轴向力作用下圆管侧向冲击示意图
1.2 材料特性
本文采用Cowper-Symonds提出的考虑钢材应变率效应的Cowper-Symonds模型进行计算,其动态屈服函数为
(1)


图2 锤体尺寸平面图
1.3 网格划分、边界条件及界面处理
为保证求解速度,薄壁圆管和落锤均以10 mm为网格尺寸的基准,楔形锤体在整个冲击过程中变形很小,故定义为刚体.共划分5 832个单元,共10 757个节点.边界条件为一端固定,一端可纵向移动,便于施加轴向压力.在模型中分别定义接触的法向方向和切向方向,圆钢管与冲击锤之间的法向接触定义为硬接触(Hard Contact).圆钢管与落锤发生接触产生切向摩擦力,库伦摩擦系数取用钢材与钢材表面常用的摩擦系数0.2.
1.4 荷载的施加
荷载的施加包括两部分:轴压力的施加和冲击荷载的施加.将落锤初始位置设置在构件附近,并为构件赋予初始速度的方式加载冲击荷载;为真实地模拟轴力对薄壁圆管的影响,需在构件受冲击荷载之前施加轴力,并在冲击过程中基本保持轴力不变.荷载的施加实际上是轴向压力与冲击力的耦合,模拟过程分为三部分.
(a)为圆钢管施加足够大的轴向力.由于圆钢管在结构中受到的轴向压力多为静力荷载,Step分析步中采用静力加载轴向力.圆钢管施加足够大轴向力的目的是确定钢管在轴力作用下屈服时弹簧加载的端部位移.在结果文件中取出一端反力和另一端弹簧位移,得到端反力达到屈服压力(P=πDtσy)时的弹簧位移Δ.
(b)为圆钢管施加轴压比为n的轴向力.同样采用静力加载轴向力,弹簧端位移取为nΔ.启动Restart命令,将有限元模型的冲击力、应力-应变和变形的计算结果输入到Restart文件中.
(c)为圆钢管构件施加横向冲击荷载,对冲击力和轴向压力进行耦合分析.在新建的圆钢管受冲击力模型中建2个Step,由于冲击是动力加载,故2个分析步均采用(Dynamic,Explicit).第一个分析步是将(b)中得到的Restart文件导入到冲击模型中,冲击锤的初始位置设定在圆钢管上方5 mm的位置,保证了落锤撞击钢管之前轴向力就已经施加到圆钢管上.第二个分析步是为圆钢管施加冲击荷载,在Load中为落锤定义速度.本有限元模型不考虑重力加速度对钢管和落锤的影响.
2 抗冲击性能分析
2.1 破坏模态
图3给出了在相同的低速冲击荷载作用下,不同大小轴压比n作用的最终变形模态和跨中截面最终变形比较图,从图3可以看到,3种轴压力作用下的变形,整体弯曲变形较小,以落锤冲击构件上表面的局部凹陷为主,且轴压力越大,凹陷量越大.
比较n=0和n=0.25的最终变形模态可以发现,在低轴压力作用下,轴压力对构件的最终变形影响不大,而比较n=0和n=0.5轴压力作用下构件的最终变形模态,发现轴压力增加到一定量后,对最终的变形影响较大.

图3 不同轴压力作用下的变形模态比较
2.2 冲击力时程曲线
冲击力是衡量钢管抗冲击性能的重要指标.图4给出了在冲击能量相同时,轴压比分别为0、0.25和0.5时圆钢管的冲击力时程曲线对比图.

图4 不同轴压力作用下的冲击力时程曲线
从图4可以看出,不同轴压比作用下的冲击力时程曲线都是经历了3个阶段:迅速加载、平台值和卸载3个过程.随着轴向压力的增加,落锤与圆钢管刚接触瞬间的最大冲击力逐渐增大,这主要是因为施加了轴向压力将试件压缩,相当于增加圆钢管的两端约束.而且随着轴向压力的增加,冲击力平台值逐渐降低,冲击持续的时间逐渐增加,冲击力衰减的速度越慢.因为圆钢管受撞击后出现横向挠度,轴压力的施加使试件产生P-δ效应,降低了试件的承载能力.
另外,有轴向力相对于无轴压力的冲击力曲线在冲击过程中震荡显著,这主要是由于施加轴向力的弹簧不可能实现完全刚性,在冲击过程中会随着圆钢管受撞击纵向尺寸的改变而伸长或缩短,进而使试件受到轴向力的大小不断改变,造成冲击力曲线在冲击过程中持续震荡.
2.3 变形时程曲线
图5给出了轴压比分别为0、0.25和0.5时圆钢管构件跨中截面顶点的位移时程曲线.

图5 不同轴压力作用下的位移时程曲线
从图5可以看出,随着轴压比的增加,构件跨中位置的挠度逐渐增加.落锤冲击试件后跨中挠度开始向下逐渐发展,然后落锤冲击速度降低,位移曲线度逐渐平缓,跨中挠度增长缓慢,随后试件和冲击锤的速度降为零,这时跨中挠度达到最大.试件产生的变形有塑性变形和弹性变形,之后试件将储存在其中的弹性势能释放出来,试件的弹性变形恢复,跨中挠度开始降低,由于在模拟冲击过程中存在摩擦,试件最终保持静止,挠度达到最终值.
2.4 耗能分析
为衡量冲击过程中构件的能量转换,对钢管顶点的荷载-位移曲线进行积分得到冲击过程中各轴压比作用下分别耗散的能量(图6).在落锤冲击构件的过程中,系统的动能逐渐转化为构件变形耗能.而构件变形耗能主要由两部分组成:一部分由构件的凹陷变形吸收;另一部分由构件的整体弯曲变形吸收.
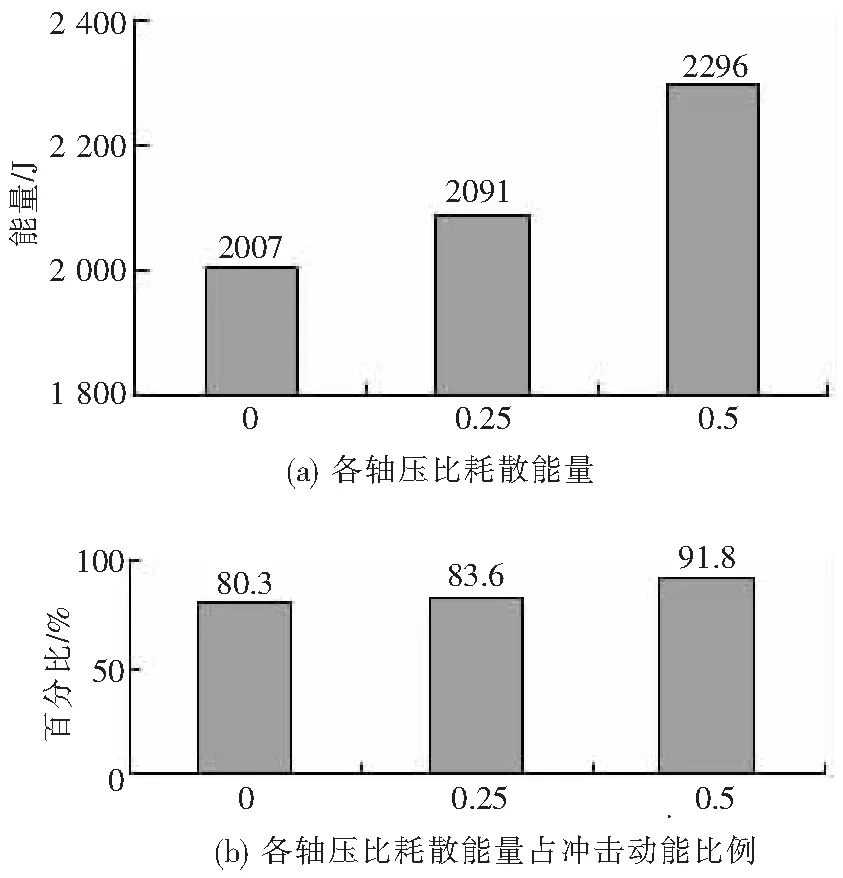
图6 各轴压比的能量耗散分析
从图6(a)中可以看到,构件变形所损耗的能量是随着轴压比的增加而逐渐增加.图6(b)为在冲击过程中钢管变形所耗散的能量占系统总能量的比例.从图6可见,随着轴压比的增加,变形耗能占总冲击动能的比例越来越大.
3 结 论
本文对一端固定一端可纵向移动薄壁圆钢管在不同轴压比作用下经受侧向冲击的动力性能进行了有限元研究,得到了以下主要结论:
(1)在低轴压力作用下,轴压力对构件的最终变形影响不大;轴压力增加到一定量后,对最终的变形影响较大.
(2)随着轴压比的增加,落锤与圆钢管刚接触瞬间的最大冲击力逐渐增大,冲击力平台值逐渐降低,冲击持续的时间逐渐增加,冲击力衰减的速度越慢.
(3)轴压比的增加,使构件跨中位置的挠度逐渐增加.说明轴向压力的施加,加剧了圆钢管相应位置挠度的增加.
(4)随着轴压比的增加,变形所耗散的能量逐渐增大,变形耗能占总冲击动能的比例越来越大.
参考文献:
[1]Johnson C K, Watson C R. Superstructure and modulation wave analysis for the unidimensional conductor hepta-(tetrathiafulvalene) pentaiodide[J]. The Journal of Chemical Physics, 1976, 64(6): 22-26.
[2]张善元, 程国强, 马宏伟,等. 受轴向冲击圆柱壳的塑性动力屈曲研究[J]. 爆炸与冲击, 2000, 20(4): 343-347.
[3]武勇忠. 多跨结构压力管道侧向冲击破坏的实验研究与计算机模拟[D].太原:太原理工大学, 2002.
[4]路国运, 雷建平, 武勇忠,等. 多跨薄壁压力管道侧向冲击破坏的实验研究[J]. 爆炸与冲击, 2003, 23(5): 454-459.
[5]雷建平, 路国运, 武勇忠,等. 压力管道受弹体侧向冲击破坏的实验研究及仿真分析[J]. 太原理工大学学报, 2003, 34(1): 1-4.
[6]王蕊.钢管混凝土结构构件在侧向撞击下动力响应及其损伤破坏的研究[D].太原:太原理工大学,2008.
[7]Zeinoddini M, Harding J E, Parke G A R. Effect of impact damage on the capacity of tubular steel members of offshore structures[J]. Marine Structure, 1998,11(4-5):141-157.
[8]Zeinoddini M, Harding J E, Parke G A R. Dynamic behaviour of axially pre-loaded tubular steel members of offshore structures subjected to impact damage[J].Ocean Engineering, 1999, 26(10): 963-978.
[9]Zeinoddini M, Harding J E, Parke G A R. Contribution of ring resistance in the behaviour of steel tubes subjected to a lateral impact[J]. International Journal of Mechanical Sciences, 2000, 42(12): 2303-2320.
[10]Zeinoddini M, Parke G A R, Harding J E. Interface forces in laterally impacted steel tubes[J]. Experimental Mechanics, 2008, 48(3): 265-280.

