集中荷载作用下架空输电导线的研究

李永平 王正运

(东北电力大学建筑工程学院，吉林 吉林 132000)

集中荷载作用下架空输电导线的研究

李永平 王正运

(东北电力大学建筑工程学院，吉林 吉林 132000)

针对大截面导线架空输电线路，从导线柔性出发，分析了传统线形方程的不足，确定了导线最低点水平张力，并对其进行算例验算，肯定了公式的可行性，在没有对导线进行简化的情况下，分析了导线在任一点作用集中荷载时导线的实际线形与弧垂，将此分析与现有的做法进行比较，得到一种全新的计算作用单个集中荷载时的线形算法。

大截面导线，线形，集中荷载，弧垂，张力

0 引言

在以往的研究中架空导线一般都在柔性条件下考虑其性能和结构特性，导线线形决定了输电线的弧垂、内力、应力等，并为线路的施工提供了重要的参数，由于导线的趋肤效应促使我们选用大截面导线进行考察，在现有的文献[1]中虽然总结出了线形方程，但是并没有完全确定其中的具体参数，其线形方程如下：

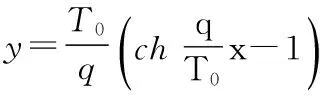
式中：T0——最低点的轴向张力； q——导线的自重均布荷载。

上式中并没给出具体的T0，显然这并不是一个真正到位的方程。针对此问题，本文对钢芯铝绞线在柔性条件下的最低点的轴力进行了计算，对后续的一系列计算提供了切实的理论依据。

1 水平张力计算

线形方程为：

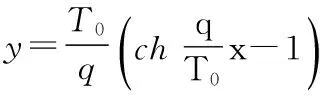
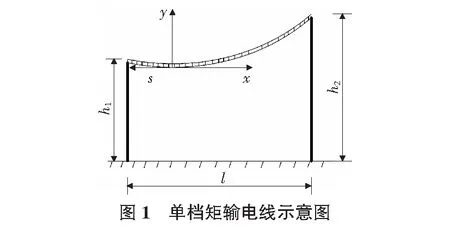
如图1所示，取导线最低点作坐标原点，利用几何关系得出平衡方程:

y(l-s)-y(-s)=h2-h1。

将条件代入线形方程得出：

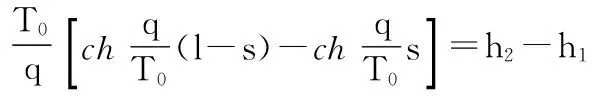
令导线最终变形为Δl，初始放线时长度为L，在导线上取一段微弧为ds，两塔的高度差为Δh，架空导线变形终止后的长度为：

对其积分可得：

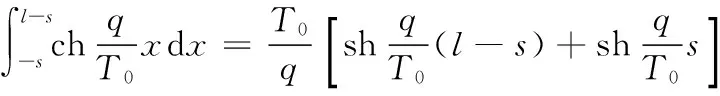
几何条件：

L′=L+Δl。

导线的变形增量为：

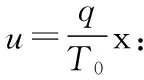
(1)

(2)

令：

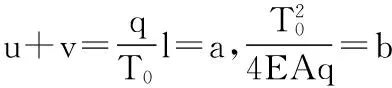
式(1)可转换为：

(3)

式(2)可转换为：

(4)

由式(4)可得：

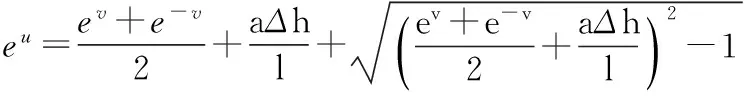
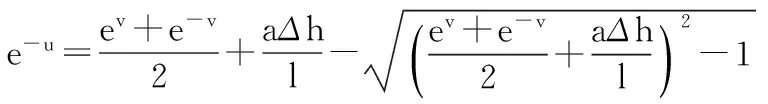
由式(3)得：

利用泰勒展开，可以求得：

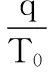
求得：

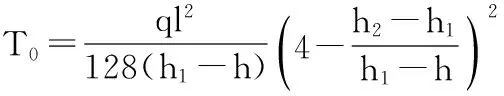
本文随后会给出具体的算例，对公式进行验证。

2 线形及弧垂的计算

2.1 计算在导线任一点施加一集中荷载的线形

在实际架空线路维护中，作业人员往往会在导线上进行人工检修，这样导线上会作用一个集中荷载，该集中荷载会引起导线弧垂和应力的相应增大，使得导线弧垂不同于无集中荷载时导线的弧垂，当弧垂超过安全距离时有可能对导线上作业的人员造成致命危险。因此，在架空输电线路设计中应该考虑在导线上作用一个集中荷载下导线线形的变化及其弧垂的计算。其具体计算如下。

如图2a)所示，虚线为未施加荷载时的线形，因为施加集中力导致导线的稳定线形不再是一个光滑曲线，不妨令两段曲线分别为y1和y2。

从图中可以看出y1的线形微分方程并没有变化，只是最低点的轴向张力发生变化，对y2的计算如下：

在y2上任取一点作用一集中力p，距离坐标原点为x1，假定曲线质量均匀分布，即线密度恒定用q表示。在最低点的张力为T0，方向沿切线方向；如图2c)所示，在y2上的任一点的轴力为T，与水平成θ角，距离坐标原点为x；在集中力处y2上的轴力为T1，与水平成θ1角，y1上的轴力为T2，与水平成θ2角，y2段导线的自重为R。

由于曲线是静止的，处于平衡状态，可得：

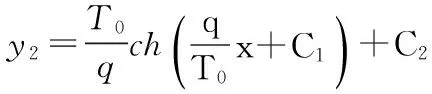
上式中有两个未知数C1，C2，需要两个已知的边界条件才可解出。边界条件如下：

当x=x1时：

y1(x1)=y2(x1)。

(5)

如图2b)所示，图为集中荷载处的受力示意图，其约束条件为：

T2sinθ2-T1sinθ1=p。

(6)

由式(5)，式(6)解出C1，C2:

C2=0。

由此得到线形：

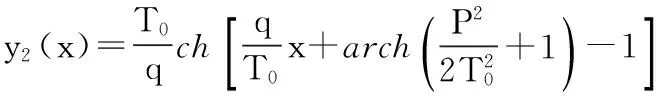
利用线形y1或y2计算集中荷载作用点处架空线路的弧垂：

2.2 现有线形方程

现有的文献[2]中对y2的求解所得线形方程表达方式如下：

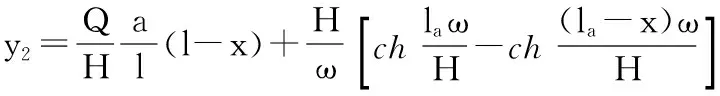
式中：Q——作用在导线上的集中荷载； H——架空线的水平张力； l——档距； a——集中荷载距坐标原点的距离； ω——架空线的均布自重荷载。

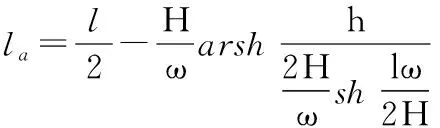
其中,h为两个悬挂点的高差。

集中荷载作用点处，架空线路的弧垂：

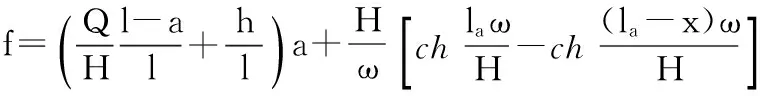
由两个公式对比可以很直接的看出，线形方程不是简单的悬链线性质，而是一个超越方程。现有文献[3]对架空输电导线作用一集中荷载时的线形求解只是简单的解析计算,并没有考虑集中荷载处导线受力的特点。本文通过微分方程，并考虑集中力处的相应约束条件确定积分常数，对作用一集中力架空线的线形求解给出了一全新的算法，对实际导线积分求解，得到的结果更加的精确。为后者计算相应的线形、弧垂、应力等提供了一定的理论依据。

3 对导线最低点水平张力的实例计算

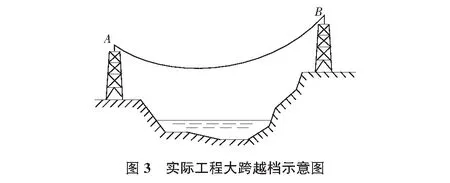
以一个实际工程为例进行说明。某220kV线路的大跨越档，导线是LGJ-240/30，档距500m，悬挂点高差80m，如图3所示。导线初始放线长度L=507.93m，导线的q=9.222N/m，计算该导线最低点水平张力。

根据导线型号可以查表得出：

E=78 480N/mm2，A=275.96mm2。

根据上面推导的公式可以得出：

T0=27 044.08N。

S=-181.29m。

由结果可以得此档距的导线最低点距离左侧悬挂点距离为181.29m，最低点的水平张力为27 044.08N。

4 结语

1)通过对导线柔性悬链线方程分析，可以看出其并没有确切的给出水平张力T0，本文计算了输电导线最低点的水平张力，使其方程得到完善。并对导线最低点水平张力进行实际算例检验，由此得出本文所得公式的可行性。

2)给出了在导线任一位置作用一集中荷载时的线形方程，并且计算了相应的弧垂。和现有的线形做出了比较，现有文献[1]中只是把导线看作柔性线，而本文从实际导线出发，把集中力处受力特点考虑到计算线形中是本文的创新点所在，得到一种全新的线形算法。

[1] 邵天晓.架空送电线路的电线力学计算[M].第2版.北京：水利电力出版社,2003.

[2] 李博之.具有单个集中荷载的平丘地段架空线计算(二)[J].电力建设，1992(6)：50-51.

[3] 李博之.大跨越档架空线索弧垂的研究[J].电力建设,2001(9)：30-32.

[4] 孔 伟.单个集中荷载作用下架空线张力计算[J].东北电力技术,2000(4)：37-38.

[5] 王战利.单个集中荷载作用下架空输电线路弧垂计算的探讨和应用[J].河南科技,2012(12)：77-78.

Study on and calculation of overhead transmission lines under single concentrated load

LI Yong-ping WANG Zheng-yun

(SchoolofConstructionEngineering,NortheastDianliUniversity,Jilin132000,China)

In view of large cross-section wire for overhead line. Starting from the wire flexible, by analyzing the deficiencies of the traditional linear equations, calculated axial tension force of the wires’ lowest point, and in the absence of wire used for the simplified case, lead role any single concentrated load is analyzed when the conductor is the actual linear and sag. The analysis compared with existing practices, sag after the lead role in a single concentrated load calculation accuracy was improved.

large cross-section conductor, linear, concentrated load, sag, tension

1009-6825(2014)03-0052-03

2013-11-11

李永平(1956- )，男，教授； 王正运(1989- )，男，在读硕士

TU312

A