基于ATVFD和EEMD的滚动轴承故障特征频率提取方法研究
段玉波 杨文涛 刘继承 蒋 锐
(东北石油大学,黑龙江 大庆 163318)
滚动轴承是旋转机械中应用最广泛的基本组成部件,也是易损零件,据统计,机械故障中70%是振动故障,其中30%的故障都与滚动轴承有关[1],轴承的使用周期过短会影响机械设备的正常生产[2]。旋转机械在生产运行中其振动信号是混在强噪声环境下的非平稳随机信号,传统的傅里叶变换并不能满足针对这类非线性、非平稳信号的分析需要。1998年由Huang N E等提出一种新的时频分析法(Hilbert-Huang Transform,HHT),能够有效地对非线性、非平稳信号进行分析,同时具有良好的自适应性[3]。HHT在机械故障诊断领域已得到广泛的应用,并取得了良好的效果,但存在一些不足,如HHT的核心内容经验模式分解(Empirical Mode Decomposition,EMD)产生模态混叠,影响分析结果。为了克服这一缺点,WU Z H和Huang N E提出了EMD方法的改进——集合经验模式分解(Ensemble Empirical Mode Decomposition,EEMD),利用高斯白噪声具有频率均匀分布的统计特性,使信号在不同尺度上具有连续性,从而有效地解决了模态混叠问题[4]。但是,EEMD算法中核心方法依旧是EMD方法,其端点效应问题仍旧存在而且计算速度和精度不高。笔者提出一种基于自适应时变滤波分解(Adaptive Time Varying Filter Decomposition,ATVFD)和EEMD相结合的新方法,使分解结果更加准确,且避免了端点效应带来的影响,通过HHT边际谱提取出故障特征频率。实验结果表明,笔者提出的方法能够应用于滚动轴承的故障诊断[5,6]。
1 HHT基本原理①
HHT方法分析信号有两个基本步骤[7,8]:
a. 使用EMD分解把信号分解成固有模态函数(Intrinsic Mode Function,IMF),其需要满足两个条件,即在整个数据中,其极值点个数和过零点的数目相等或最多差一个;在任意点,由局部极大值构成的上包络和由局部极小值构成的下包络的均值必须为零。
b. 对IMF进行Hilbert时频谱和边际谱分析。
1.1 EMD算法原理
对于信号x(t),计算所有信号的极大值和极小值,用三次样条插值函数拟合出上包络线u(t)和下包络v(t),得到平均曲线:
(1)
从而得到第一个IMF分量h1(t):
h1(t)=x(t)-m1(t)
(2)
这时h1(t)可能不满足IMF定义,需要再次筛选:
h11=h1(t)-m11(t)
(3)
重复式(3)直到满足筛选停止准则0.2 (4) 将式(3)重复k次得到: h1k(t)=h1(k-1)(t)-m1k(t) (5) 此时h1k就是第一个IMF分量,表示为C1(t)=h1k(t),则残余信号为: r1(t)=x(t)-C1(t) (6) 以r1作为待分析信号,重复以上步骤直到所得剩余部分为一单调信号或其值小于给定值时,分解完毕,得到所有IMF分量C2(t)、C3(t)、C4(t),…,Cn(t)以及残余分量Rn(t),这时信号可表示为所有IMF分量和残余量之和: (7) 对各个IMF分量进行希尔伯特变换,可以得到解析信号(不考虑残余量)和其时频谱(信号幅度在三维空间的时间-频率函数)为: (8) (9) 边际谱定义为: (10) 边际谱是对信号中各个频率成分的幅值的整体度量,它表示了信号在概率意义上的累积幅值,反应了信号的幅值在整个频率段上随频率的变化情况。在某个频率ω存在幅值,代表在信号的整个时间长度上,很可能有这样一个频率的波动在局部出现过,h(ω)越大,代表ω出现的可能性越大。就机械设备实际情况而言,既然有能量存在,就必定有能量的根源——振动冲击存在,也就是说轴承在运作过程中对其损伤部位有冲击力作用。 首先,识别出信号x(t)所有局部均值点,并组成一个时间序列{e(ti)},其中ti表示第i个局部极值点的时间[9]。对于连续3个局部极值点e(ti),e(ti+1)和e(ti+2)使用三抽头时变滤波器计算ti+1时刻的局部均值m(ti+1),则: m(ti+1)=h(ti)e(ti)+h(ti+1)e(ti+1)+h(ti+2)e(ti+2) (11) 其中时变滤波器在ti、ti+1和ti+2时刻的脉冲响应值分别为: (12) (13) (14) 利用式(11)可以得到信号各局部极值点处的局部均值m(0)、m(t1)、m(t2),…,m(tn),再使用三次样条插值函数对其进行曲线拟合得到局部均值m1(t),以后处理步骤与EMD相同。 ATVFD算法在每次分解时只需进行一次曲线拟合,从而降低了计算量,加快了分解速度;另外,其局部均值不是由局部均值的包络所得,而是在局部极值的基础上通过时变滤波器算法得到,使分解结果更加精确;相比EMD算法,ATVFD算法的边界摆动有所改善。 在EMD算法中,得到合理IMF的能力取决于信号极值点的分布情况,如果信号极值点分布不均匀,会出现模态混叠的情况。为此,Huang N E将白噪声加入待分解信号,利用白噪声频谱的均匀分布,当信号加在遍布整个时频空间分布一致的白噪声背景上时,不同时间尺度的信号会自动分布到合适的参考尺度上,并且由于零均值噪声的特性,经过多次平均后,噪声将相互抵消,集成均值的结果即可作为最终结果[10]。 EEMD算法步骤为:首先在原始信号x(t)中加入均值为0、标准差为常数(通常为原始信号标准差的0.1~0.4倍)的白噪声n(t),即xi(t)=x(t)+ni(t)。 再对第i次加入高斯白噪声的信号xi(t)进行EMD分解,得到IMF分量Cij(t)与余项ri(t),其中Cij(t)为第i次加入高斯白噪声后,分解得到的第j个IMF分量。 然后重复以上步骤N次,利用不相关的随机序列的统计均值为零的原理,将上述对应的IMF进行总体平均运算,消除多次加入高斯白噪声对IMF的影响,最终得到EEMD分解后的IMF分量为: (15) 此时EEMD的分解结果为: x(t)=∑jcj(t)+r(t) (16) 笔者提出的ATVFD-EEMD分解方法步骤如图1所示。原始信号分解前加入均值为0、标准差通常为原始信号标准差的0.1~0.4倍的白噪声n(t),对加入噪声后的信号进行ATVFD分解,得到IMF分量Cij(t),其中i表示加入高斯白噪声次数,cj表示集总平均后得到的j个IMF分量。 图1 ATVFD-EEMD分解方法步骤 最后ATFVD-EEMD的分解结果为: x(t)=∑jcj(t)+r(t) (17) 滚动轴承故障诊断实验使用QPZZ-Ⅱ旋转机械振动模拟实验平台,针对支撑轴承内圈损伤故障进行实验研究。实验时,交流变频电机转速为2 148r/min,使用型号为HRB-N205EM的轴承,其参数见表1(由表1数据可计算出内圈损伤故障特征频率f=256.11Hz)。实验测得的原始信号时域曲线如图2所示。 表1 HRB-N205EM轴承参数 图2 原始信号时域曲线 对实测信号分别进行EMD分解和ATVFD分解求出第一次分解的均值曲线如图3所示。从图3中可以看出,在左端点处EMD算法曲线有严重的抖动,端点效应严重;而ATVFD在左右端点都具有良好的均值曲线。 图3 EMD和ATVFD方法计算出均值曲线对比 对原始信号分别进行EMD分解和ATVFD-EEMD分解,用两种方法分解出的IMF分量如图4a、b所示,对IMF分量信号计算出的边际谱如图5a、b所示。 图4 用两种方法分解出的IMF分量及其余项 图5 对IMF分量信号计算出的边际谱曲线 通过图5可以看出,ATVFD-EEMD算法与EMD算法相比,EMD算法的边际谱曲线在频率260.0、50.0、100.0Hz附近出现较大的振幅,这说明在EMD分解过程中出现端点效应和模态混叠问题,从而影响边际谱的曲线,导致无法准确判断滚动故障诊断其故障类型;而笔者提出的ATVFD-EEMD算法的故障频率为255.6Hz,不仅在精度和准确度上有较大优势,而且其边际谱曲线只在频率255.6Hz附近出现较大振幅,有效地抑制了边界效应和模态混叠问题,可以准确判断出故障位置和故障类型。 笔者分别介绍了EMD、ATVFD和EEMD分解算法理论,针对EMD和EEMD方法的不足,提出一种基于ATVFD-EEMD的新方法。从滚动轴承内圈故障信号的分析实验可以看出,笔者提出的方法同时具有ATVFD方法分解精度高、抑制边界效应的优势,和EEMD分解可避免模态混叠的优点,从而有效、准确地提取出了振动信号滚动轴承内圈故障频率。1.2 Hilbert变换的时频谱与边际谱
2 改进的ATVFD-EEMD算法原理
2.1 ATVFD算法
2.2 EEMD算法原理
2.3 改进的ATVFD-EEMD算法
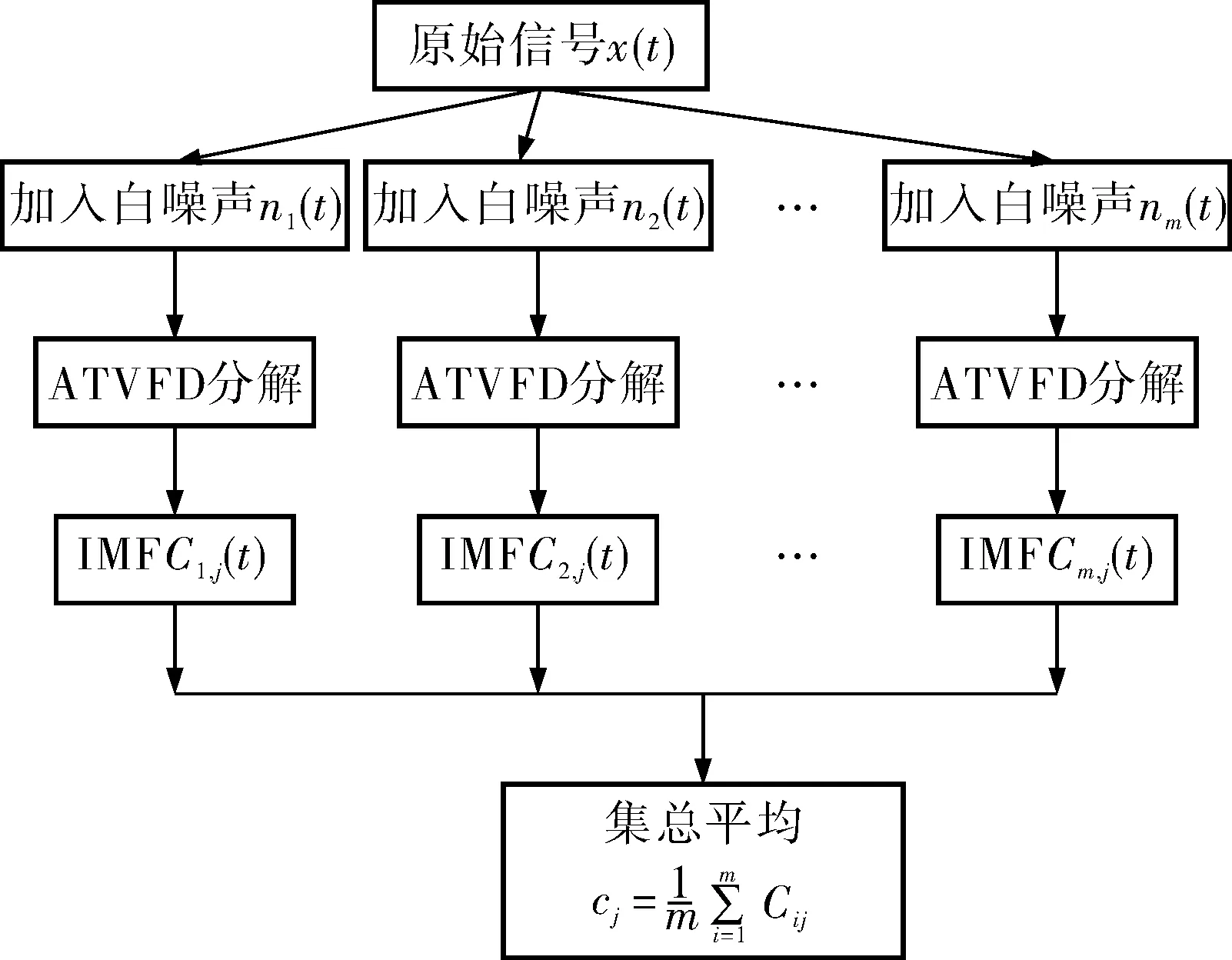
3 基于ATVFD-EEMD的滚动轴承故障诊断实验

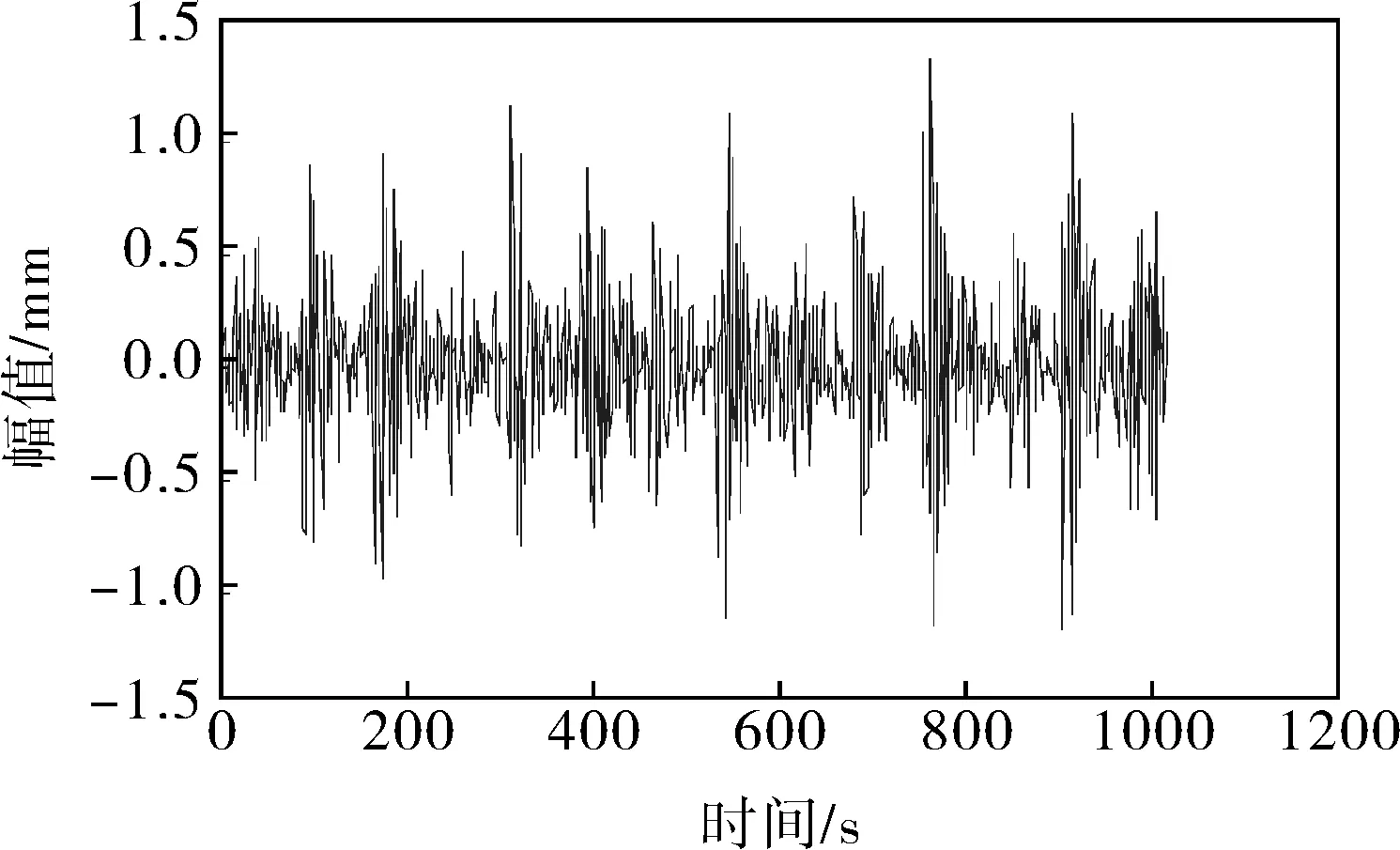
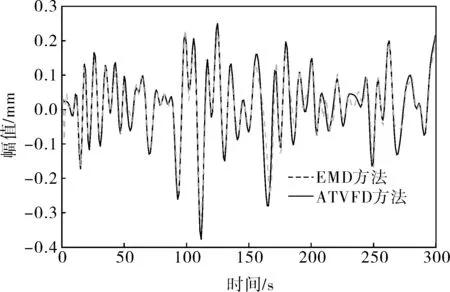

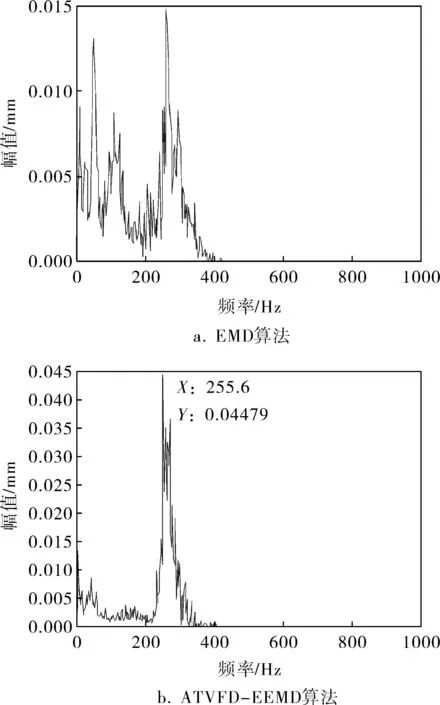
4 结束语

