基于小波包与PCA遗传神经网络相结合的齿轮箱故障诊断方法

罗 毅 甄立敬

(华北电力大学控制与计算机工程学院，北京 102206)

齿轮箱是风电机组的关键部件，也是机组中故障发生率最高的部件，故障百分比已超过60%[1]，齿轮箱一旦发生问题维修非常不便。因此，加强对风电机组齿轮箱的监测和故障诊断，对降低风电场维护费用和提高风电场运行的经济效益具有重要意义。

齿轮箱故障诊断已成为目前国内外热门的研究课题之一。郭艳平等通过小波分析等方法诊断了其故障类型和部位，但是小波分析只是对低中频段部分做了分解，而机组的故障特征信号也存在于高频信号中[2]。小波包分解能够较好地提取出振动信号在各个频带上的特征信息，并通过这些频带上的信息表征齿轮的运行状态[3]。笔者采用小波包提取时频域特征值。宋崇智等建立了基于改进Elman神经网络的齿轮箱故障诊断模型，虽然该方法具有收敛快且能避免局部最小的优点，但是只提取频域特征值作为神经网络的输入[4]。笔者充分考虑故障与时域和时频域特征值之间的因果关系，选择提取时域和时频域特征值。龙泉等提出了一种基于粒子群优化BP神经网络风电机组齿轮箱故障诊断方法，有一定的实用性，但是选择的输入之间具有一定的相关性[5]。主成分分析法可以用较少的互不相关的综合变量来反映原变量所提供的绝大部分信息，笔者利用主成分分析法消除相关性，确定主成分，从而减少神经网络的输入变量[6]。张新海和雷勇介绍了BP神经网络在机械故障诊断中的应用及实例[7]。BP神经网络具有较强的非线性拟合能力，遗传算法是一种高效、并行且全局搜索的方法[8]。

笔者利用遗传算法与神经网络结合能有效地解决传统BP网络的收敛速度慢、易陷入局部极小值的缺陷，并提高网络的学习精度[9，10]。提出了一种小波包和PCA遗传神经网络相结合的风电机组齿轮箱故障诊断方法。该方法选取振动信号的峭度和峰值作为时域特征值，利用小波包算法提取频带能量和二范数作为时频域特征值。利用主成分分析法消除特征值之间的相关性，得到的新变量作为神经网络的输入。利用遗传算法对BP神经网络权值和偏置进行优化，建立遗传神经网络对故障进行诊断。

1 小波包与PCA遗传神经网络结合算法①

1.1 小波包分解

小波包算法是一般化的小波变换，对信号的低、高频都需要进行分解，弥补了小波分析的不足[11]，齿轮箱发生故障时不同故障类型的振动信号在相同频带内信号的能量和二范数会发生变化，它使得一些频带内的信号能量有增大或减小的趋势，因此，在各频带成分信号的能量和二范数中包含着丰富的故障信息。所以笔者选用利用频带能量和二范数来构造振动信号的特征向量，其构造过程如下：

a. 利用db小波对采集来的信号S(t)进行三层小波包分解，从而获得从低频到高频的8个小波包分解系数。

b. 对小波包分解系数进行单节点重构，提取8个频带范围的重构信号S3j(j=0，1，…，7)，它分别包含了故障信号从低频到高频的信息。

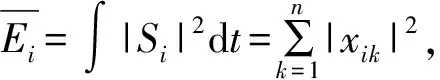
d. 特征向量的构造。齿轮箱发生故障会直接导致振动信号时域特征参数的变化。为了有效反映齿轮箱的运行状态，通常组合选用若干个时域特征参数进行故障诊断，笔者采用峭度xkur和峰值xp两个时域特征参数作为振动信号的特征量[12～14]。构造振动信号的一个18维特征向量x=[xp，xkur，E0，E1，E2，E3，E4，E5，E6，E7，A0，A1，A2，A3，A4，A5，A6，A7]，从而得到故障特征特征样本矩阵。

1.2 主成分分析

笔者构造的振动信号特征向量与齿轮箱故障有较确定的因果关系，为消除特征向量x元素间的相关性，利用主成分分析法，降低特征向量x的维数，用较少的互不相关的综合变量反映原变量所提供的绝大部分信息，通过对新变量的分析达到解决问题的目的，从而减少神经网络的输入变量[15]。设有n组数据，特征向量R的维数为p，即每组数据包含p个变量，得到故障特征样本矩阵Xn×p，主成分分析法简化输入的过程如下[16，17]：

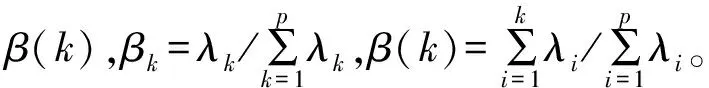
d. 求出主成分Z=Yα，若∀α∈(0,1)，且当β(s)≥α，则Z1,Z2，…，Zs称为样本X1,X2,…,Xp的显著性水平为α的主成分。其中β(s)为第s个主成分累计贡献率。以Z1,Z2,…,Zs来代替X1,X2,…,Xp，既降低了输入维数又消除了原样本空间的自相关性。

1.3 遗传神经网络建模

笔者采用遗传算法优化神经网络的初始权值和阈值，分两步进行：首先利用遗传算法群体寻优策略，采用遗传算法对网络权值和阈值进行全局搜索，保证其落入全局最优点的领域；然后用L-M法对网络权值和阈值进行细化训练以进一步减小误差，使其收敛于全局最优解或性能更好的近似最优解。该网络能够充分发挥遗传算法的全局收敛和L-M算法的指导性搜索思想。

笔者选用的BP网络采用三层神经元结构，即一个输入层、一个隐含层和一个输出层。输入层神经元为Z1,Z2,…,Z12；输出层为齿轮箱12个部件的状态T1,T2,…,T12，正常为0，故障为1，根据遗传神经网络的输出就可以诊断出故障类型。遗传神经网络结构如图1所示。

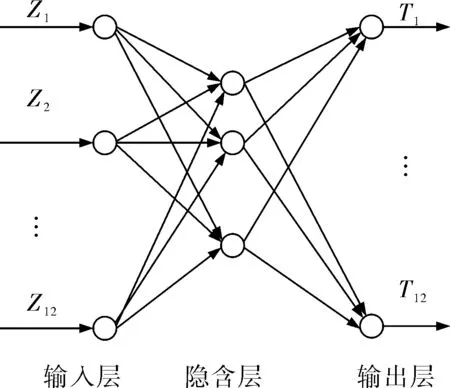
图1 遗传神经网络结构

笔者提出的小波包和PCA遗传神经网络相结合算法，先利用小波包分解得到故障特征样本矩阵Xn×p，然后利用主成分分析得到新变量矩阵Zn×s，最后利用遗传神经网络得到输出向量T，根据向量T即可得到齿轮箱的故障类型。小波包与PCA遗传神经网络结合算法的流程如图2所示。

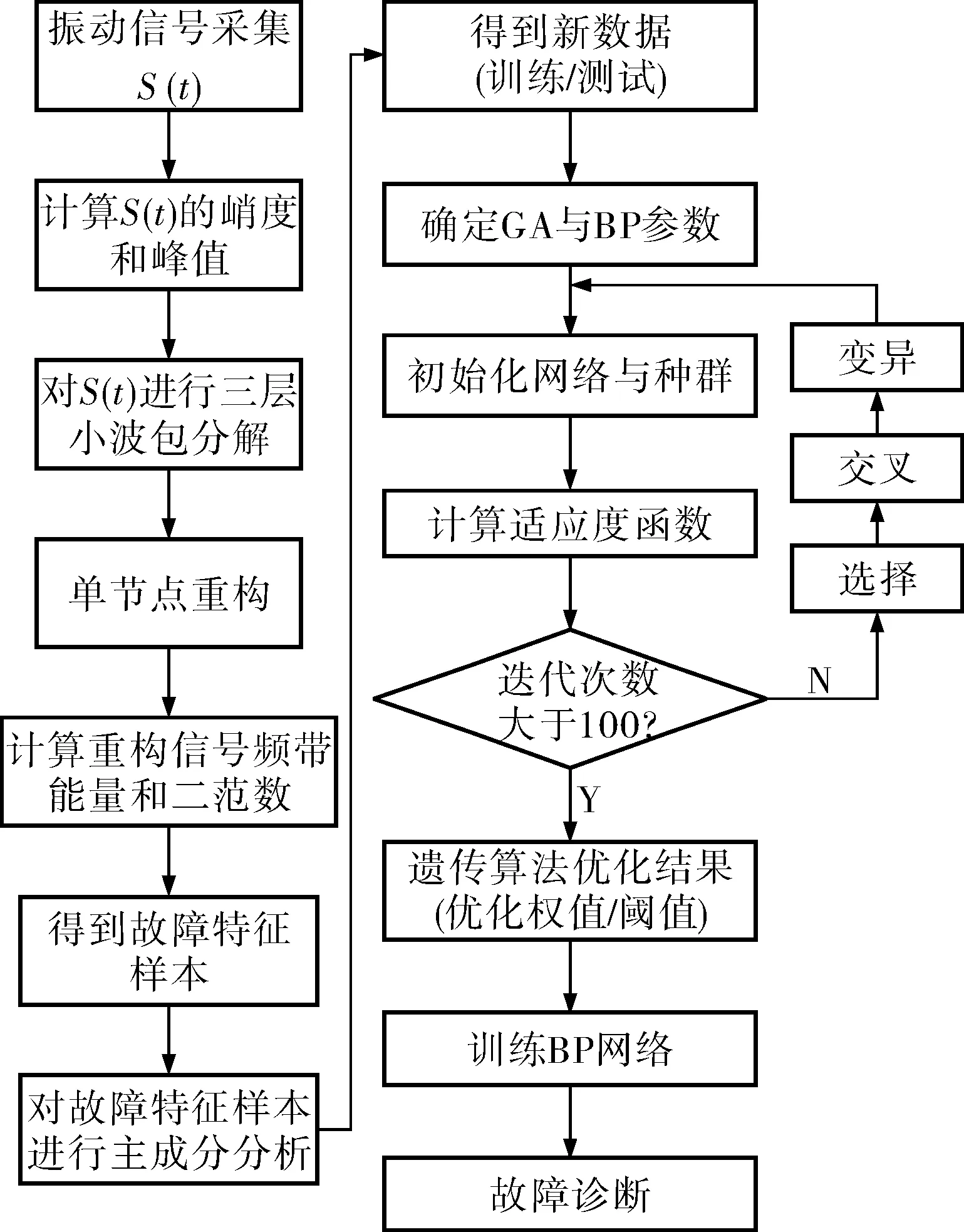
图2 小波包与PCA遗传神经网络结合算法的流程

2 仿真测试

2.1 实验系统简介

风电机组齿轮箱的主要结构包括轴、齿轮和轴承。故障从结构上可以分为：轴的故障(轴不对中、轴不平衡及轴弯曲等)、轴承故障(轴承内/外圈磨损及滚动体磨损等)和齿轮故障(齿面剥落、齿面胶合、齿面磨损及断齿等)。笔者选用的被测设备为某风电场的风电机组齿轮箱，被测设备为工业通用齿轮箱，齿轮箱结构如图3所示。

图3 风电机组齿轮箱结构

在齿轮箱前、后端轴承上安装加速度传感器，齿轮箱输入轴安装转速故障实验在某公司的机械故障综合模拟实验台上进行，通过换轴承、齿轮或轴可以改变故障类型，这样可以达到模拟齿轮箱故障的目的，从而得到不同故障类型时的振动信号。采集齿轮箱的加速度振动信号，采样频率为66.7kHz。笔者选取齿轮箱7种故障类型(表1)进行分析，每种故障选取40组样本作为训练数据，3组样本作为测试数据，以此作为原始数据样本。表1中IS为输入轴、OS为输出轴、ID为从动轴、IS为输入侧、OS为输出侧。

表1 齿轮箱故障类型

2.2 利用小波包和主成分分析处理数据

笔者对7种故障类型的振动信号进行分析，利用三层小波包变换提取频带能量和二范数作为时频域特征值，提取峰值和峭度作为时域特征值，构造振动信号的一个18维特征向量，每种故障振动信号下的特征样本各43组，故得到故障特征矩阵X301×18，X301×18的部分数据列于表2。

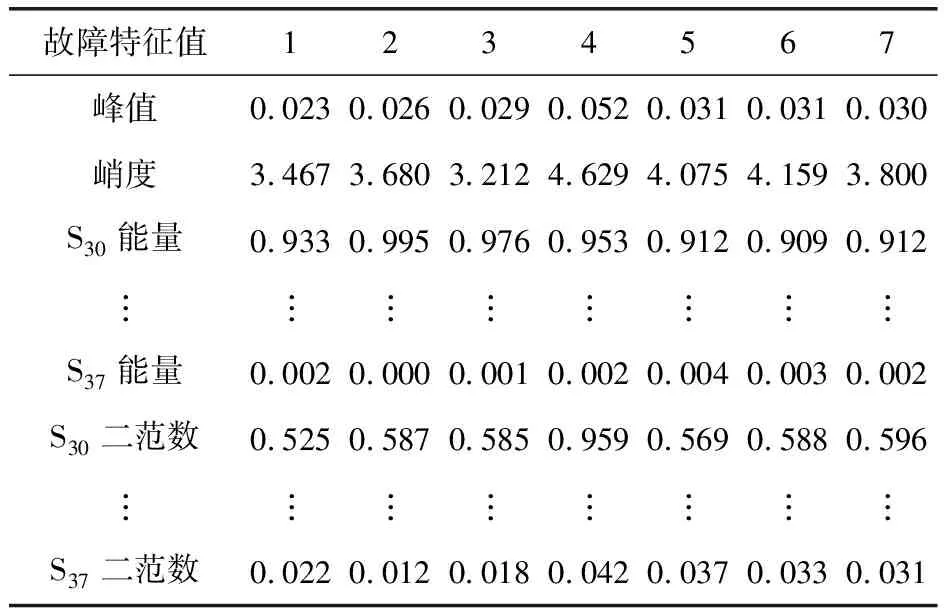
表2 风电机组齿轮箱故障特征值样本

为消除故障特征样本X301×18各变量单位和数量级不同的影响，先对X301×18进行标准化理，得到新的数据矩阵Y301×18，然后对矩阵Y301×18进行主成分分析，可得到新变量协方差矩阵特征值表(表3)。取α=95%，由表3可知β(4)≥α，则以Z1，Z2，Z3，Z4来代替X1，X2，…,X18，得到4个新的综合指标变量，这样既降低了输入维数又消除了特征值间的相关性。

表3 新变量的协方差矩阵特征值

2.3 利用遗传神经网络进行故障诊断

BP神经网络的输入为经主成分分析后确定的新变量，输入层神经元个数为4，输出为齿轮箱12个部件的状态，输出层神经元个数为12；将隐含层神经元个数设为输入层神经元个数的两倍再加一[18]。学习速率为0.01，训练目标为0.01。遗传算法在进化搜索过程中是以适应度函数为依据的，笔者选取误差平方和的倒数作为适应度函数；权重个体的基因位数较长，所以采用浮点数编码；初始种群大小为100；选择轮盘赌抽样；算术交叉概率为0.90；非统一变异概率为0.09；最大进化代数为100代。每种故障类型各选取40组样本作为训练样本，用280组样本对网络进行训练。

主成分分析后所得数据作为神经网络的输入，利用遗传算法优化神经网络的初始权值和阈值，经过100代繁殖后，退出遗传算法，得到神经网络权值和阈值的初始值，优化过程如图4所示。

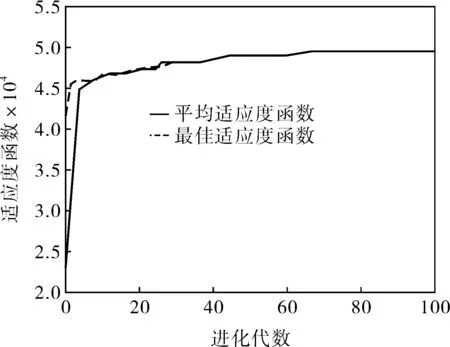
图4 适应度函数进化曲线

从图4可以看出，遗传繁殖到72代时，最佳适应度函数已不再发生变化，即说明遗传算法已对神经网络的权值和阈值进行了全局搜索，找到粗略的最优值区域。找到粗略的最优值区域之后，为进一步减小误差，对神经网络采用L-M算法进行细化训练。完成网络的建立和训练后，每种故障类型各选取3组样本对网络进行测试，部分输出的故障诊断结果见表4。

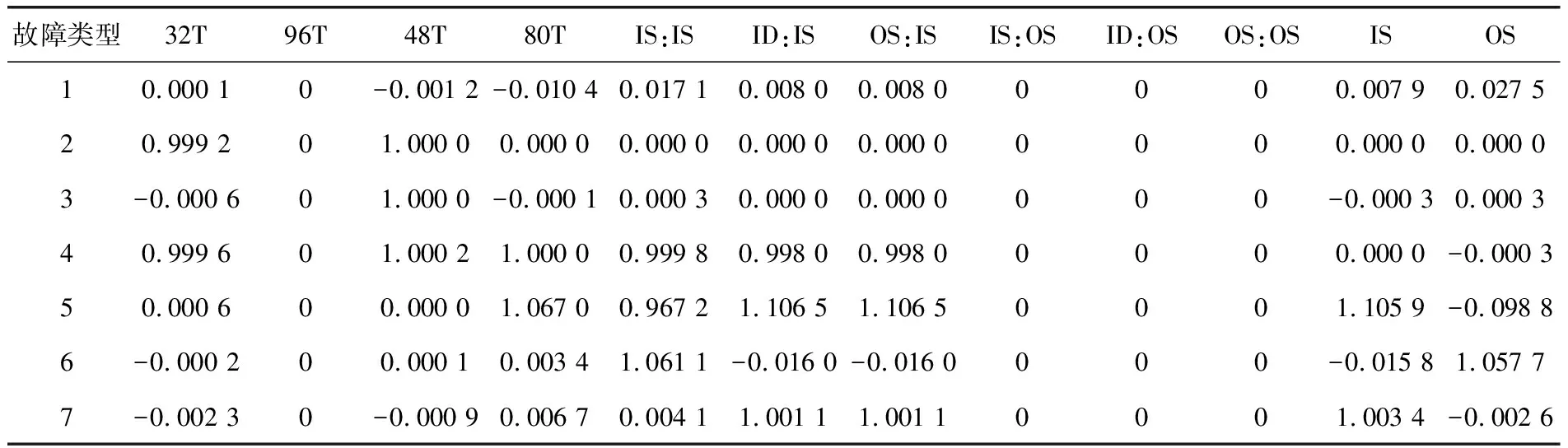
表4 状态识别结果

从表4的数据可判断出第一组数据为正常状态，第二组数据为32T磨损、48T偏心，第三组数据为48T偏心，第四组数据为32T磨损、48T偏心、80T断齿、输入轴承内圈磨损、从动轴承滚动、输出轴承外圈磨损，第五组数据为80T断齿、输入轴承内圈磨损、从动轴承滚动、输出轴承外圈磨损、输入轴不对中，第六组数据为输入轴承内圈磨损、输出轴歪曲，第七组数据为从动轴承滚动、输出轴承外圈磨损、输入轴不对中。

2.4 结果分析

为了进一步说明小波包与PCA遗传神经网络相结合算法的有效性，实验比较了不同算法下的平均故障识别率，分类器均采用BP神经网络，实验结果见表5。由表5可知，笔者所采用的小波包与PCA遗传神经网络相结合算法对风电机组齿轮箱故障诊断的结果准确、精度高。

表5 故障识别率 %

注：TFD为时频域特征值，即提取的小波包频带能量和二范数；TD为时域特征值，即提取的峭度和峰值。

3 结束语

笔者提出的小波包与PCA遗传神经网络相结合算法诊断结果准确，精度高。该方法选取振动信号的峭度和峰值作为时域特征值，利用小波包算法提取频带能量和二范数作为时频域特征值。利用主成分分析法消除18个特征值之间的相关性，确定主成分，作为遗传算法优化的BP神经网络的输入，进行故障诊断。仿真测试表明了算法的有效性。