一种抗混叠小波变换在电力系统谐波检测中的应用

刘继承 董青松 张 琳

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

近年来随着电力系统飞速发展，系统中的谐波对电力系统环境造成的破坏也越来越严重，不但影响了整个电力系统的电气环境，而且对系统本身和广大用户也造成了不小影响，所以对谐波的治理具有明显的社会和经济效益[1～3]。传统的谐波检测方法有快速傅里叶变换(FFT)和短时傅里叶变换(STFT)，FFT算法能精确地检测整数次谐波，但不能检测非整数次谐波，而且伴有频谱泄漏和栅栏现象；STFT算法通过窗函数有效降低了频谱泄漏次数，但是由于窗函数的不变性，无法自适应调整，分辨率很低。

为了克服FFT和STFT的局限性，引入了小波变换。Mallat S将塔式算法思想应用到小波分析中，使小波变换有了突破性的发展。在正交小波基构造的基础上，将信号分解为不同频道，再将分解后的信号进行重构，由此提出了快速算法——Mallat算法[4，5]。但是在Mallat算法中产生的频率混叠现象对谐波检测的精度有很大的影响，笔者采用一种改进的单子带重构快速算法，降低了小波分解与重构过程中产生的频率混叠。

1 多分辨分析与小波Mallat 算法①

多分辨分析理论的提出为小波正交基构造提供了一种简便的方法，也为正交基小波快速算法奠定了理论基础。多分辨分析是指空间L2(R)内一系列子空间序列{Vj}j∈Z称为L2(R)的一个多分辨分析，并满足如下条件[6]:

a. 单调性，…⊆Vj-1⊆Vj⊆Vj+1⊆…，∀j∈Z；

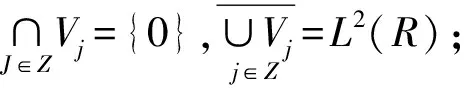
c. 平移不变性，f(x)∈V0⟹f(x-k)∈V0,∀k∈Z；

d. 伸缩性，f(x)∈Vj⟺f(2x)∈Vj+1,∀j∈Z；

e. Riesz基存在性，存在g∈V0，使得{g(x-k)|k∈Z}构成V0的Riesz基。

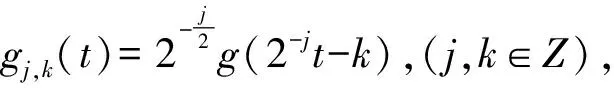
设Wj是Vj和Vj+1内的正交补空间，则满足关系式：Vj+1=Vj⊕Wj，(j∈Z)，其中⊕表示子空间之和。由此多分辨分析的子空间Vj可以用有限个子空间来逼近，即有：

Vj=Wj-1⊕Vj-1=Wj-1⊕Vj-1⊕Vj-2=…

=Wj-1⊕Wj-2⊕…W0⊕V0

(1)

若令fi∈Vj表示分辨率为2j的函数逼近，dj∈Wj表示逼近的误差，则式(1)等价为：

fj=fj-1+dj-1=fj-2+dj-2+dj-1=…=f0+d0+d1+

…+dj-2+dj-1

(2)

设f=fj，则式(2)可表示为：

(3)

由式(3)可知，在空间L2(R)中函数f可以根据分辨率20时f的低频部分和分辨率2i(i∈[0，j-1])时的f高频部分完全重构，这就是著名的Mallat塔式重构算法的思想。设Ajf为f∈L2(R)在分辨率2j下的近似，则Ajf可以进一步分解为f在分辨率2j-1下的近似Aj-1f(由低通滤波器H得到)，与位于分辨率2j-1与2j之间的细节Dj-1f(通过高通滤波器G得到)之和，Mallat塔式重构算法分解过程如图1所示。

图1 Mallat塔式重构算法分解过程示意图

重构过程是分解过程的逆过程，重构过程如图2所示。

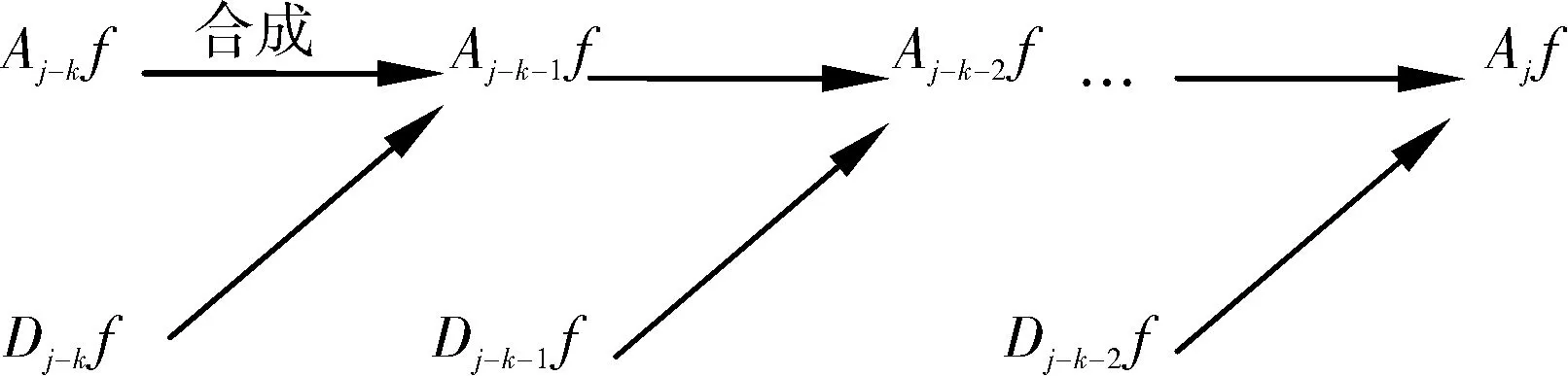
图2 Mallat塔式重构算法重构示意图

Mallat算法是由分解滤波器H、G和重构滤波器h、g构成。H、h为低通滤波器，与尺度函数相对应；G、g是带通滤波器，与小波函数相对应。Mallat算法即是将信号的频带二进划分成一系列子带的过程，各子带的频带范围与信号的采样频率有关。Mallat分解算法所得到的只是小波系数，将所得到的小波系数再重构出原始信号。由于滤波器的非理想截止特性，而且在各尺度的高频子带隔点采样时不满足采样定理，在小波系数作傅里叶变换后的频谱中，会有一些多余的频率分量。在实际操作中，理想的滤波器是不存在的，在运用Mallat算法时，在分解过程中会用到隔点采样，在重构过程中，会用到隔点插零，如果是理想滤波器的情况下，两次的频率折叠恰巧能够相互抵消，但在处理一些庞大的复杂信号时，这种缺陷就不可忽视，将会严重影响重构后信号的效果，这样对谐波检测分析有很大的影响。

2 单子带重构算法

单子带重构算法可以改善Mallat算法中的频率混叠问题。单子带重构算法的分解过程和Mallat算法中的分解部分是一样的，即得到各尺度上的小波系数；在重构过程中单子带重构算法将得到的小波系数分别重构至与原信号相同尺度。

运用单子带重构算法分析一个实例，并对实例进行仿真测试。设实例信号s为：

s(t)=sin(40πt)+sin(80πt)+sin(120πt)+

sin(160πt)+sin(200πt)+e-6tsin(240πt)

(4)

如图3所示为实例信号波形，图4所示为其频谱。以400Hz作为采样频率取实例信号2 048个点，选用sym5小波，对实例信号进行三层尺度分解并重构，结果如图5所示(a表示低频，d表示高频)。

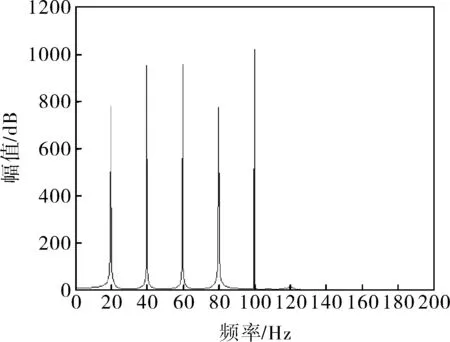
图4 实例信号的频谱

图5 单子带重构算法对实例信号s的小波分析

从图4中可以看出，实例信号由20、40、60、80、100Hz和瞬时频率120Hz组成。理论上对实例信号进行小波变换的结果见表1。

表1 实例信号s小波变换理论结果 Hz

从图5中可以看出，在对实例信号第一层分解中低频部分a1含有20、40、60、80、100Hz频率成分，分解效果较好，但在高频部分d1中含有80、120Hz频率成分，多出了80Hz的频率成分；在第二层低频部分a2中含有20、40、60Hz的频率成分，在高频部分d2中含有40、60、80、100、120Hz的频率成分，多出了40Hz、60Hz的频率成分；在第三层低频部分a3中含有20Hz频率成分，高频部分d3中也含有20Hz频率成分。从以上的分析可以看出单子带重构算法在处理信号分频时产生了严重的频率混叠现象。

单子带重构算法总体上看相当于滤波，它是将信号分解到一系列二进制划分的频带上的过程[7]。在分解与重构中，隔点采样中的频率混叠在隔点插零中得到纠正。得到的子信号与原信号有相同的采样频率。单子带重构算法相对于Mallat算法在对谐波信号处理中对信号的重构效果有很大的提高，由于小波滤波器的非理想截止性使得频率混叠现象不能避免。因此，单子带重构算法还需要进一步的改进。

3 改进的单子带重构快速算法

在单子带重构算法中产生频率混叠的原因是小波滤波器的非理想截止性和在各尺度高频子带隔点采样不满足抽样定理。设想如果去掉多余的频率成分，在重构算法中就可以避免频率混叠。由此引入一种方法，利用快速傅里叶变换和快速傅里叶逆变换去掉各子带上多余的频率部分，称这个方法为改进的单子带重构快速算法。算法如图6所示。

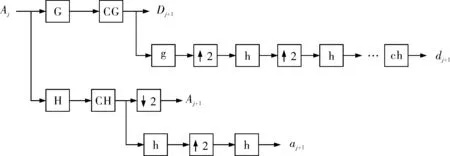
图6 改进的单子带重构快速算法

(5)

(6)

(7)

4 改进的单子带重构快速算法的实例验证

仍然采用式(4)所示的实例，并对其运用单子带重构快速算法处理，并进行仿真测试，进而验证改进的单子带重构快速算法在消除频率混叠时的效果。以400Hz作为采样频率取实例信号2 048个点，选取N为4时的Daubechies小波，对实例信号运用改进的单子带重构快速算法处理后的频谱如图7所示。

在图7中，对实例信号的第一阶尺度重构信号中，低频部分a1中含有20、40、60、80、100Hz的频率成分，在高频部分d1中含有100Hz和120Hz的频率成分；在第二阶尺度重构信号中，低频部分a2中含有20、40Hz的频率成分，在高频部分d2中含有60Hz和80Hz的频率成分；在第三阶尺度重构信号中，低频部分a3中几乎就是20Hz的正弦信号，高频部分也只是40Hz的正弦信号。对实例信号的三阶重构频谱图的分析结果与表1的理论值几乎相吻合，由此可以证明改进的单子带重构快速算法去除了单子带重构算法中的频率混叠现象。

图7 改进的单子带重构快速算法的小波分析

5 运用单子带重构快速算法对谐波信号的处理

笔者取一段具有一定周期性的谐波信号，取采样频率为2 000Hz。图8所示为谐波信号的时间波形及其频谱图。

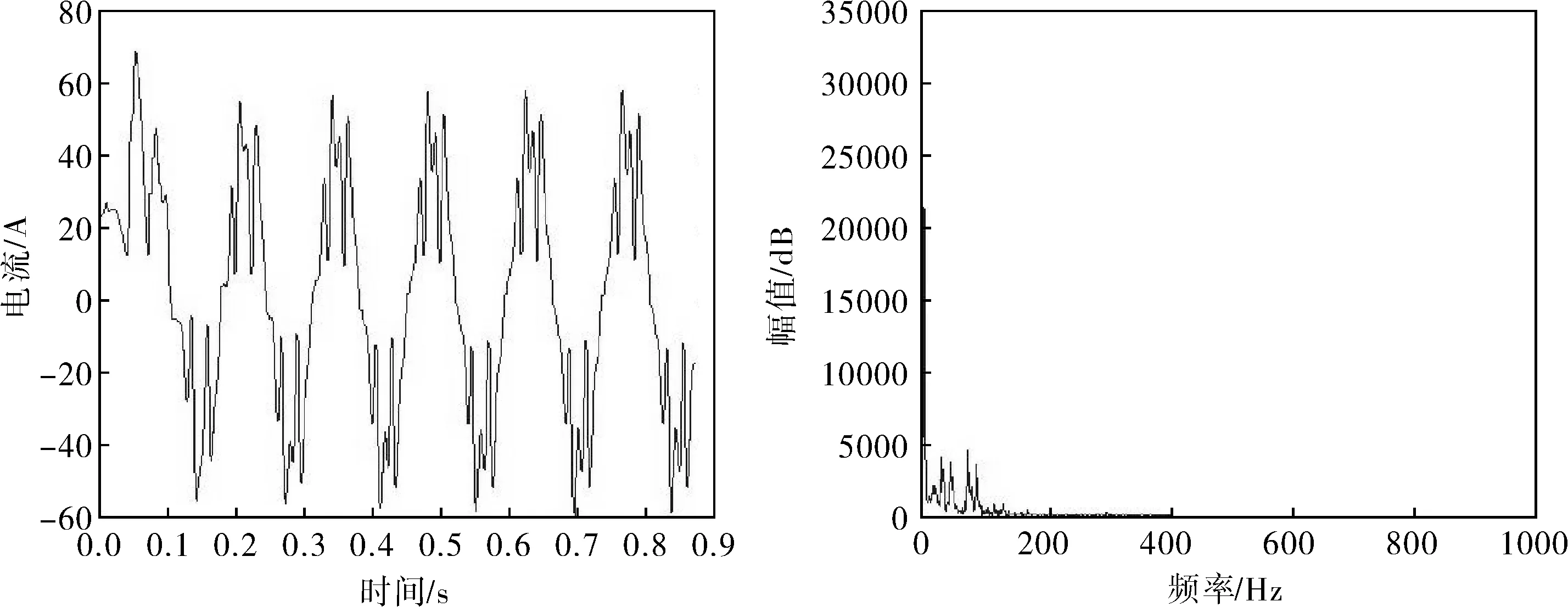
图8 谐波信号的时间波形及其频谱

选取具有紧支集的正交小波Daubechies5对原始信号进行三层小波分解[8]。首先用单子带重构算法对谐波信号进行处理(图9)，然后用改进的单子带重构快速算法对其进行处理(图10)。

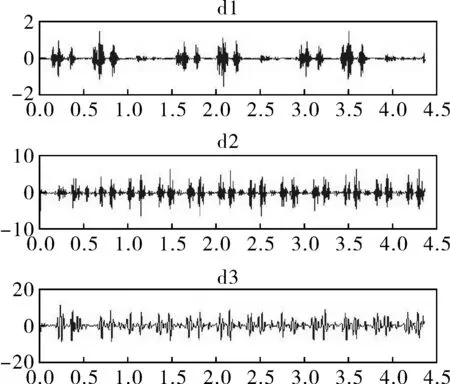
图9 单子带重构算法处理的谐波信号

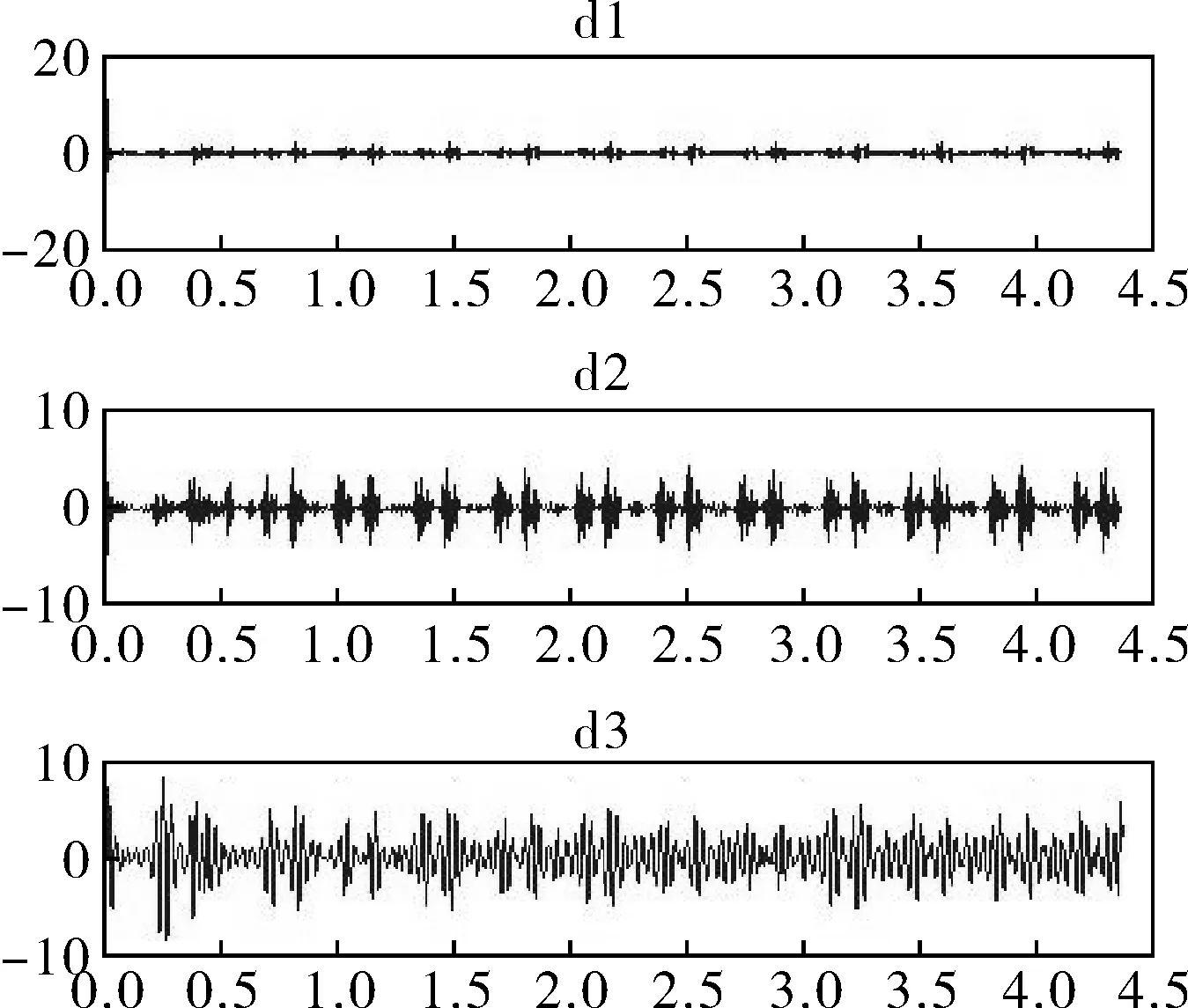
图10 改进的单子带重构算法处理的谐波信号

图9、10是对谐波信号三阶分解后的高频部分，其中图9是用单子带重构算法处理的，从图9中可以看出周期性的谐波信号仍存在频率混叠现象，在d1、d2中可以明显地看出有冲击频率成分。图10为运用了改进的单子带重构算法的高频部分，图中d1、d2已经基本上可以看出周期性的谐波信号，冲击频率成分也有很大的改善。由此可以看出改进的单子带重构快速算法已经有效地消除了处理谐波信号中频率混叠的现象，该算法可以高效并精准地重构出谐波信号，达到检测谐波信号的目的，为消减电力系统中的谐波信号提供了有利条件。

6 结束语

笔者通过改进的单子带重构快速算法，有效地消除了信号分解与重构过程中的频率混叠现象。将改进的单子带重构快速算法应用于对电力系统的谐波检测中，不但有效地抑制了分解和重构过程中频率混叠的问题，而且减小了在重构过程中产生的误差，处理后的结果可以分辨出谐波信号。该方法在对电力系统中的谐波检测上将会有很广阔的应用。