线性回归方法在核数据处理中的应用
吕健雄,李 鑫,程道文
(1.长春工业大学软件职业技术学院,吉林 长春 130012;2.长春工业大学基础科学学院,吉林 长春 130012)
线性回归方法在核数据处理中的应用
吕健雄1,李 鑫1,程道文2
(1.长春工业大学软件职业技术学院,吉林 长春 130012;2.长春工业大学基础科学学院,吉林 长春 130012)
在核数据处理中,为减少统计涨落引起的误差,在函数关系已知的条件下用线性回归方法计算,在函数关系未知的条件下用线性回归方法寻找待测量的计算公式.以中子感生瞬发γ射线分析方法测量水泥生料元素含量为例,线性回归方法可以准确地确定热中子通量以及Si,Al,Fe和Ca含量.计算结果显示,计算出来的热中子通量的平均偏差为0.31%,4种元素的测量精度都达到GB/T 176-2008(水泥化学分析方法)的要求.
核数据处理;线性回归方法;统计涨落;中子感生瞬发γ射线分析方法
在放射性测量中,即使所有实验条件都稳定,在相同时间内对同一对象进行多次测量,每次测得的γ计数并不相同,而是围绕某个平均值上下波动.此现象被称为放射性γ计数的统计涨落,是放射性原子核衰变的随机性引起的.另一方面,原子核衰变发出的粒子被探测器接收的γ计数也存在统计涨落.所以核数据处理不是简单的解方程,在很多问题中需要用线性回归方法以减少统计涨落引起的误差.
中子感生瞬发γ射线分析(NIPGA)技术已经发展为一项成熟的元素分析技术,并相继用于水泥、煤炭、石油等行业以及毒品、爆炸物的检测[1-5].由于中子与待测样品的多种原子核发生弹性散射、非弹性散射、热中子俘获、放出带电粒子等核反应,在处理这些核数据时很难用理论推导出样品内快中子通量、热中子通量、元素含量等计算公式.为了寻找这些计算公式,本文以NIPGA技术测量水泥生料元素含量为例,根据实际数据设计模拟了30个水泥生料样品,然后用多元线性回归找出热中子通量计算公式以及Si,Al,Fe和Ca 4种元素含量的计算公式.
1 线性回归的原理
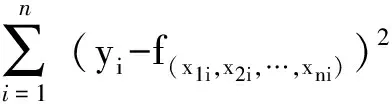
(1)
2 利用线性回归方法计算相关系数
衰变常数测量、放射性活度测量等都可以看做函数关系已知求相关系数的问题.以衰变常数测量为例,放射衰变遵循下列定律[7]
Nt=N0e-λt.
(2)
(2)式中λ是衰变常数,N0是0时刻的原子核数.Nt是经过时间t后还存留的原子核数,虽然无法直接测量,但可以利用衰变产生的粒子数对其估算.如果实验条件确定,Nt与衰变产生的粒子(如α,β,γ)数成正比,即
Nt=knt.
(3)
(3)式中k是常数,nt是t时刻测得的衰变产生的粒子数.把(3)式带入(2)式并取自然对数得
lnnt=-λt+b.
(4)
(4)式中b=lnN0-lnk,测量几组nt和t,就可以线性回归出衰变常数.
3 利用线性回归方法确定函数表达式
在核技术应用中用线性回归寻找函数表达式的例子非常多,本文以NIPGA技术测量水泥生料元素含量为例.在测量时,中子与水泥生料样品内的原子核发生热中子俘获反应,并释放出特征γ射线.当实验设备和待测元素确定后,基本计算公式为[8-9]
G=k(N/φ)+b.
(5)
(5)式中:N和G分别是待测元素的含量以及该元素的特征γ射线计数;k和b是待测常数;φ是样品所在区域的热中子通量,中子源产额一定时,φ与样品内的元素含量有关.D-D中子发生器释放的中子能量为2.5 MeV,在样品内经过多次碰撞才能慢化为热中子,很难用理论推导出φ的计算公式.Si,Al,Fe,Ca和O是水泥生料的主要元素,质量分数之和超过93%.所以在中子产额一定时,可以简单地认为φ是这5种元素含量的函数,以计算Si为例,(5)式变为
GSi=k(N/φ(wSi,wAl,wFe,wCa,wO))+b.
(6)
3.1 热中子通量的确定
在水泥生料中,O以Si,Al,Fe和Ca的氧化物形式存在,所以氧含量是这4种元素含量的函数,不是一个独立的变量,因而φ的计算公式可以写为
φ=f1wSi+f2wAl+f3wFe+f4wCa+b.
(7)
利用Maclaurin级数,可以把(7)式写为
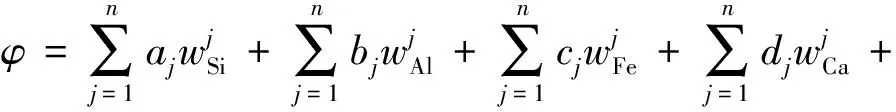
(8)
为寻找热中子通量的计算公式,根据德惠鑫雨水泥厂提供的数据,本文设计了30组水泥生料样品.在MCNP模拟中用计数卡F4计算水泥生料样品所在区域的热中子通量.表1是D-D中子发生器产额为107个/s中子,测量时间为100 s的模拟计算结果.其中Si,Al,Fe和Ca 4种元素的特征γ能量依次为4.934,3.466,7.631和6.420 MeV.
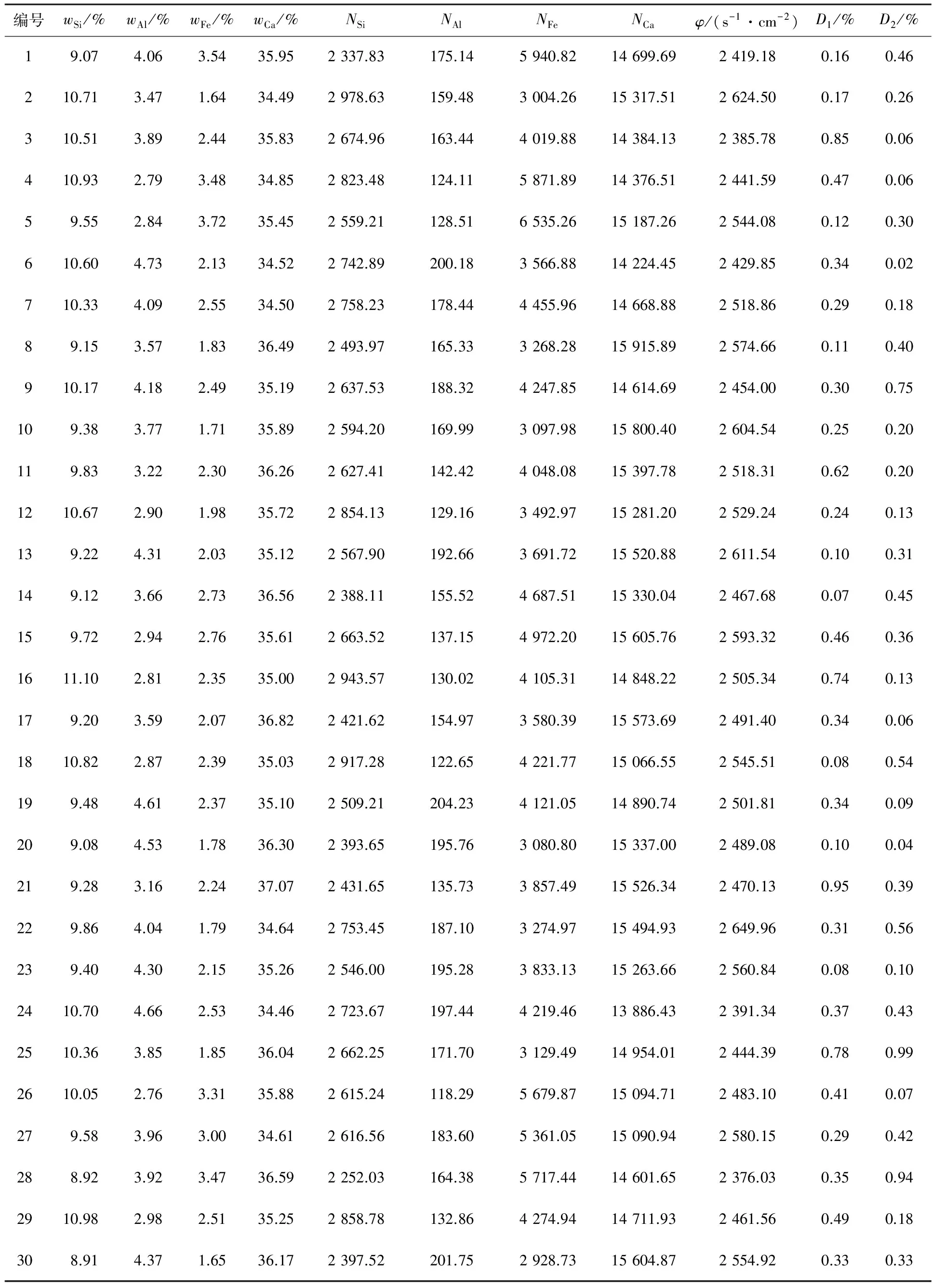
表1 水泥生料样品的元素含量及特征γ计数
表1中的wSi,wAl,wFe和wCa分别表示样品中Si,Al,Fe和Ca 4种元素的质量分数,NSi,NAl,NFe和NCa分别表示4种元素的特征γ射线计数,φ表示样品所在区域的热中子通量.
当n取1时,利用多元线性回归得到热中子通量的计算公式
φ1=-135.867×wSi-121.494×wAl-99.840×wFe-118.515×wCa+8 755.943.
(9)
利用表1中的数据以及(9)式得到样品所在区域热中子通量的计算值(用φ1表示),与φ相对偏差的绝对值D1(见表1)为

(10)
由表1可以看出,D1的平均值只有0.35%,所以可以认为(9)式所描述的热中子通量与水泥生料元素含量间的关系是比较准确的,n的取值不需要再增加.
(9)式虽然能够计算出水泥生料样品所在区域的热中子通量,但是需要知道Si,Al,Fe和Ca的含量,因而无实际应用价值.由于特征γ计数与元素含量是对应的,可以用γ射线计数代替元素含量.利用多元线性回归以及表1中的NSi,NAl,NFe,NCa和φ得到热中子通量的计算公式
φ2=0.342 82×NSi+1.829 7×NAl+0.040 685×NFe+0.187 31×NFe-1 686.7.
(11)
利用(11)式和表1中的数据可以得出水泥生料样品所在区域热中子通量的计算值(用φ2表示),与φ相对偏差的绝对值见表1中的D2.由表1可以看出,D2的平均值只有0.31%,所以(11)式所描述的热中子通量计算公式不仅准确,还有较高的应用价值.
3.2 元素含量计算公式的确定
在(5)式中,用(11)式的计算结果(φ2)代替φ,并把N/φ当做一个变量,根据表1中的数据,利用线性回归可以得到每种元素的计算公式:
GSi=9.396 5×(NSi/(0.342 82NSi+1.829 7NAl+
0.0406 85NFe+0.187 31NCa-1 686.7))+0.050 072.
(12)
GAl=56.337×(NAl/(0.342 82NSi+1.829 7NAl+
0.040 685NFe+0.187 31NCa-1 686.7))+0.020 628.
(13)
GFe=1.448 5×(NFe/(0.342 82NSi+1.829 7NAl+
0.040 685NFe+0.187 31NCa-1 686.7))-0.012 636.
(14)
GCa=5.721 4×(NCa/(0.342 82NSi+1.829 7NAl+
0.040 685NFe+0.187 31NCa-1 686.7))+1.151 6.
(15)
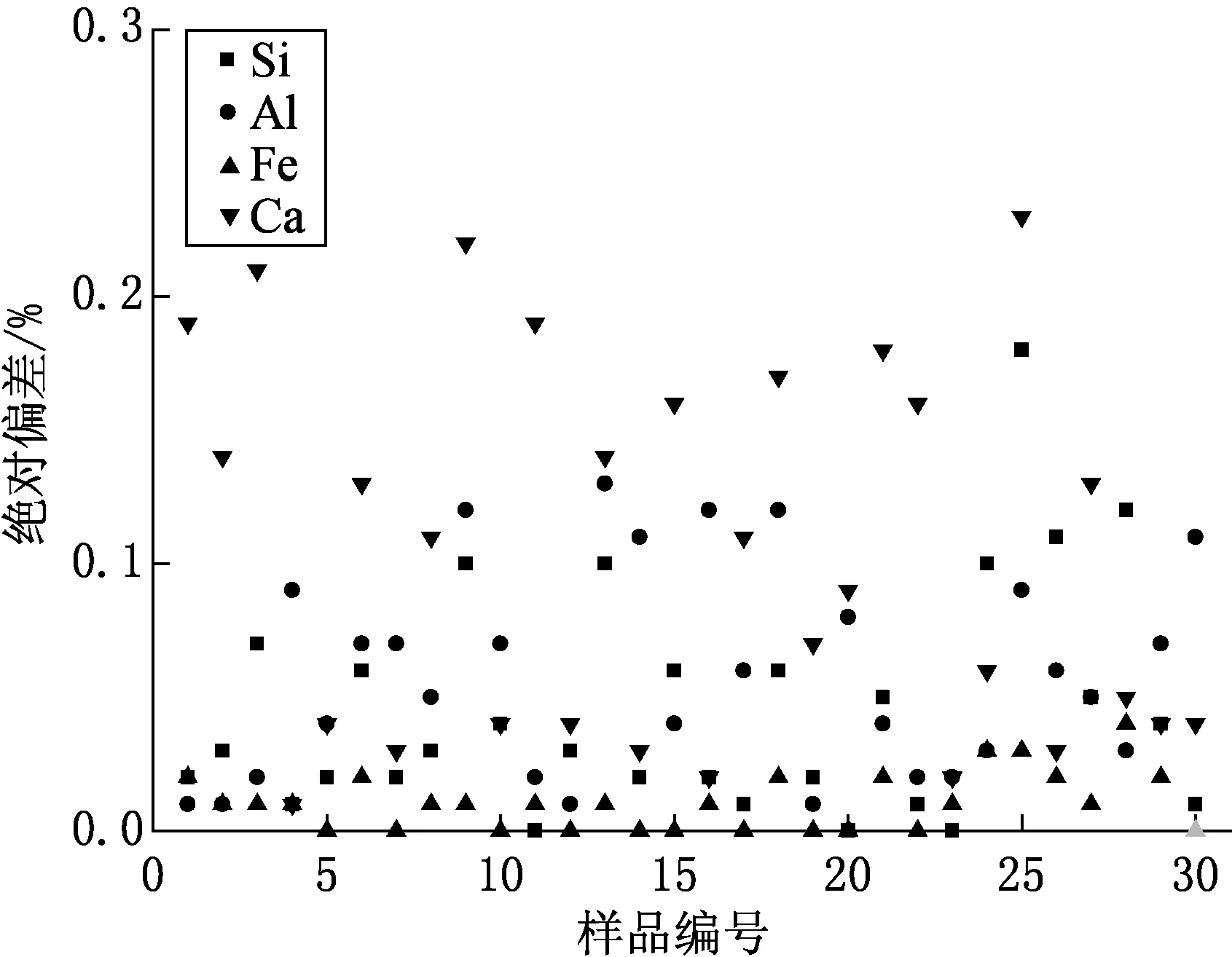
图1 计算结果的绝对偏差
利用(12)—(15)式分别计算4种元素的含量,与实际值之间的绝对偏差(即计算值与实际值之差的绝对值)如图1所示.在“水泥化学分析方法(GB/T 176-2008)”中要求Si,Al,Fe和Ca的误差不能分别高于0.20%,0.30%,0.20%和0.40%.由图1可以看出,所有样品的4种元素测量结果都达到GB/T 176-2008的要求.
4 结论
由于统计涨落的存在,核数据处理不是简单的解方程,在很多问题中需要用线性回归方法来减少统计涨落引起的误差或者寻找函数关系式.在测量衰变常数时,在函数关系已知的条件下,线性回归方法可以减小统计涨落引起的误差.用NIPGA技术测量水泥生料元素含量时,在函数关系未知的条件下,线性回归方法可以确定函数关系式.本文模拟计算了30个水泥生料样品,利用线性回归方法得到了热中子通量以及Si,Al,Fe和Ca含量的计算公式.用这些公式计算出来的热中子通量的平均偏差仅为0.31%,4种元素的测量精度都达到GB/T 176-2008(水泥化学分析方法)的要求.
[1] LIM C S,TICKNER J R,SOWERBY B D,et al. An on-belt elemental analyzer for the cement industry [J]. Applied Radiation and Isotopes,2001,54:11-19.
[2] LIM C S,ABERNETHY D A. On-line coal analysis using fast neutron-induced gamma-rays [J]. Applied Radiation and Isotopes,2005,63:697-704.
[3] HIROSHI T,FUMIO I,JUNICHI K,et al. Development of an oil-in-soil meter using neutron moderation and microwave attenuation [J]. Nuclear Instruments and Methods in Physics Research B,2004,213:540-543.
[4] KIRALY B,T SANAMI,DOCZI R,et al. Detection of explosives and illicit drugs using neutrons [J]. Nuclear Instruments and Methods in Physics Research B,2004,213:452-456.
[5] VOURVOPOULOS G,WOMBLE P C. Pulsed fast/ thermal neutron analysis:a technique for explosives detection [J]. Talanta,2001,54:459-468.
[6] 孙毅,刘仁云,王松,等. 基于多元线性回归模型的考试成绩评价与预测[J]. 吉林大学学报:信息科学版,2013,31 (4):409-414.
[7] 杨福家.原子物理学[M].北京:高等教育出版社,2006:324-325.
[8] CHENG D W,GU D S,LIU L M,et al. Improvement of the determination of hydrogen content in a multicomponent sample by D-T generator[J]. Chinese Physics C,2010,34(5):606-609.
[9] LIU Y R,LU Y X,XIE Y L,et al. Development and applications of an on-line thermal neutron prompt-gamma element analysis system [J]. Journal of Radio Analytical and Nuclear Chemistry,1991,151(1):83-93.
(责任编辑:石绍庆)
The application of linear regression method in nuclear data processing
LÜ Jian-xiong1,LI Xin1,CHENG Dao-wen2
(1.School of Software Vocational Technology,Changchun University of Technology,Changchun 130012,China;2.School of Basic Sciences,Changchun University of Technology,Changchun 130012,China)
In order to reduce the error caused by statistical fluctuation in nuclear data processing,the linear regression method is used to estimate the parameter when the function is known,and to find the function when it’s unknown. Take measuring elements contents in cement raw material by INPGA (Neutron Induced Prompt Gamma-ray Analysis) for example,the linear regression method is able to find the functions which are used to compute the thermal neutron flux and the contents of Si,Al,Fe and Ca in cement raw material. The result of the calculation shows that the average deviation of thermal neutron flux is less than 0.31% and the precisions of silicon,aluminum,iron and calcium can all meet the requirement of GB/T 176-2008 (Method for Chemical Analysis of Cement).
nuclear data processing;linear regression method;statistical fluctuation;NIPGA
1000-1832(2014)04-0072-05
10.11672/dbsdzk2014-04-013
2014-05-30
国家自然科学基金资助项目(11305019,11205069).
吕健雄(1981—),女,讲师,主要从事计算机软件与理论研究;程道文(1978—),男,博士,副教授,主要从事核技术应用研究.
TP 274+.2;O 571.53 [学科代码] 490·10
A

