中立型Logistic差分方程的Flip分支*
梁璐莎, 陈斯养
(陕西师范大学 数学与信息科学学院,陕西 西安 710062)
0 引 言
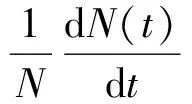
模型解的渐进性态.Gopalsamy[7]提出了如下中立型Logistic模型
文献[8-12]对其解的渐进性态做了进一步的讨论.在生态数学中,对于生命长、世代重叠并且数量很大的种群常近似采用微分方程模型,文献[13-20]讨论了多个具有时滞的连续性泛函微分方程解的渐近性态;对于生命短、世代不重叠或是生命长、世代重叠但其数量较少的种群经常采用差分方程模型.本文主要研究了具有时滞的连续中立型微分方程
对应的中立型Logistic差分方程
x(n+1)-x(n)=rx(n)(1-a1x(n)-a2(x(n+1-τ)-x(n-τ)))
(1)
当τ=1,2时正平衡态的存在唯一性和局部渐进稳定性,分支的存在性及其方向和稳定性等问题,其中r表示种群的内禀增长率,a1、a2表示种群在第n代、第n-τ代种群的密度制约系数,r、a1、a2∈R+.特别地,当a2=0时,(1)式即为经典的Logistic模型.
1 正平衡态稳定性与分支存在的条件
本节讨论模型(1)在τ=1,2两种情况下正平衡态的稳定性以及分支存在的条件.
1.1 τ=1时正平衡态稳定性与分支存在条件
将(1)写作
(2)
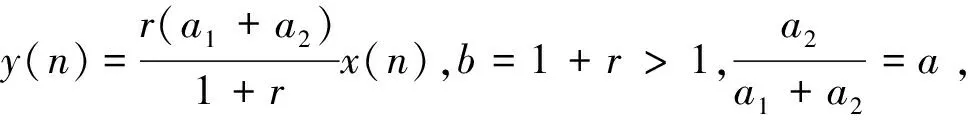
y(n+1)=by(n)(1-y(n)+ay(n-1))
(3)
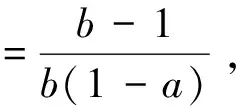
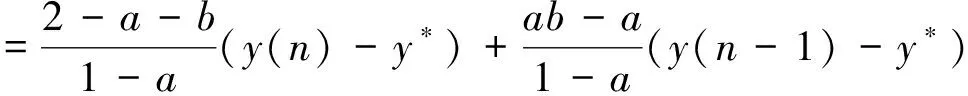
(4)
所以(4)对应的特征方程为
(5)
下面应用Jury判据[21]给出模型(3)正平衡态局部渐近稳定的条件.
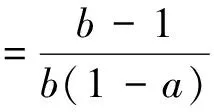
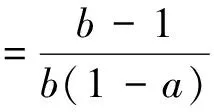
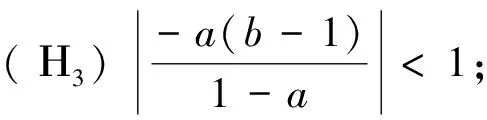
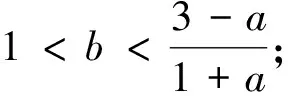
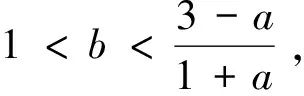
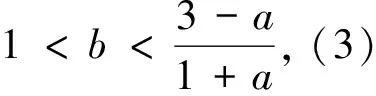
1.2 τ=2时正平衡态稳定性与分支存在条件
当τ=2时,(1)式为
(6)
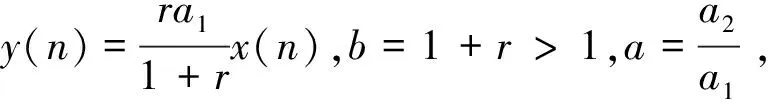
y(n+1)=by(n)[1-y(n)-ay(n-1)+ay(n-2)]
(7)
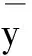
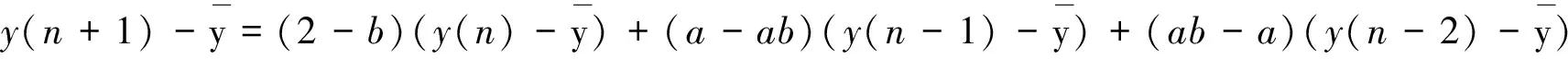
(8)
则(8)的特征方程为
p(λ)=λ3-(2-b)λ2-(a-ab)λ-(ab-a)=0
(9)
根据文献[21],得到模型(7)正平衡态局部渐近稳定的条件.
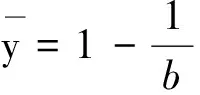
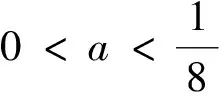
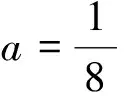
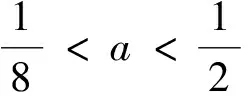
证明:根据文献[21],若模型(7)满足如下三个条件:
(Η1)|-2+b-ab+a|<1-a+ab;(Η2)|a-ab|<1;(Η3)|1-(ab-a)2|>a(b-1)2
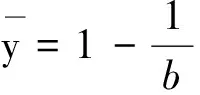
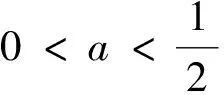
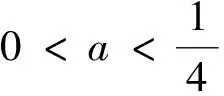
以下对定理3中(1)的情况给出产生分支的条件,情况(2),(3)的分支条件可同理给出.
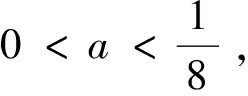
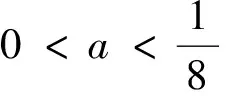
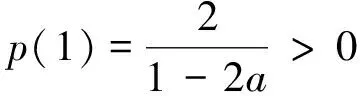
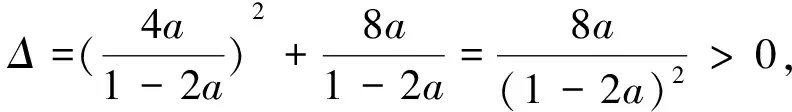
2 分支的方向以及稳定性和规范形
本节选取种群的内禀增长率r做无量纲变化后对应的参数b作为分支参数,利用分支理论和中心流形定理讨论模型(3)和(7)Flip分支的方向和稳定性,应用文献[22]中的投影方法计算其中心流形.
2.1 τ=1时分支的方向以及稳定性和规范形
τ=1时,将(3)式做如下变化:
(10)
(10)式在平衡态E(y*,y*)的临界Jacobi矩阵
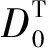
为了应用文献[22]中的投影法计算中心流形,现将系统(3)化为如下形式
(11)
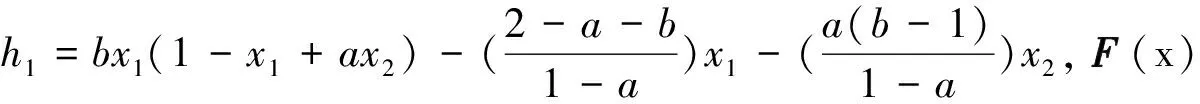
B(x,y)和C(x,y,z)在坐标下的分量分别为:
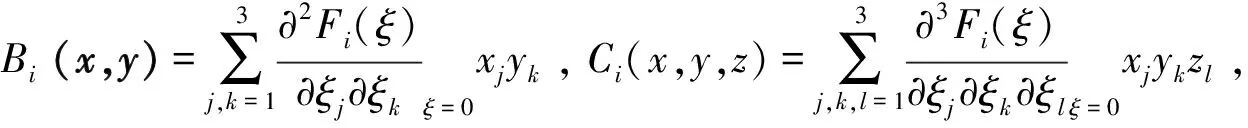
η→-η+cη3+O(η4),
其中临界规范性系数c决定反转分支的非退化性,且可以预测周期2环的分支方向,系数c由下面公式给出:
(12)
根据以上理论,经计算得
B(x,y)=(-2bx1y1+ab(x1y2+x2y1),0)T,C(x,y,z)=0
将p,q代入上式可得
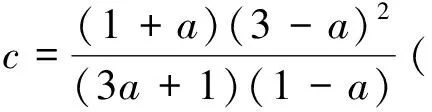
(13)
根据文献[22],可得如下定理:
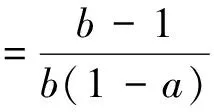
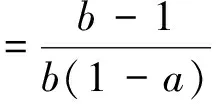
2.2 τ=2时正平衡态稳定性与分支存在条件
将(7)式做如下变化:
(14)

如下应用文献[22]中的投影法计算中心流形,将系统(7)写为如下形式
其中g1=bx1(1-x1-ax2+ax3)-(2-b)x1-(a-ab)x2-(ab-1)x3.类似2.1中计算可得
B(x,y)=(-2bx1y1-ab(x1y2+x2y1)+ab(x1y3+x3y1),0,0)T,C(x,y,z)=0
将p,q代入上式可得
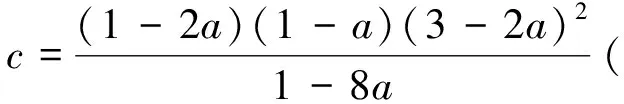
(14)
根据文献[22],可给出如下定理6.
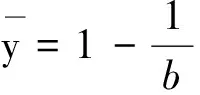
3 数值模拟
下面通过两个举例,运用Matlab软件绘出模型解的图形,验证以上结论与条件的可实现性,并说明该模型动力学行为的复杂性.
例1τ=1时,最大Lyapunov指数图以及取a=0.124 5,b0=2.557 1时,模型(3)随b变化的分支图(图1),取b=2.507 1
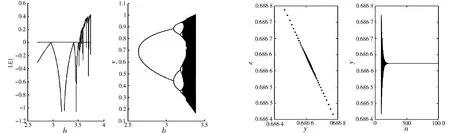
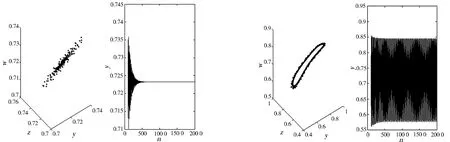
图1随b变化的最大Lyapunov指数图和分支图(τ=1)图2b=2.507 1 Fig.1 The maximum Lyapunov exponent and bifurcation Fig.2 Stability solution map (b=2.507 1 map vs.the parameterb 图3 b=2.567 1>b0周期解图(τ=1) 图4 随b变化的Lyapunov指数图和分支图(τ=2) 例2τ=2时,最大Lyapunov指数图以及取a=0.124 5,b1=3.663 1时,模型(7)对应随b变化的分支图(图4),b=3.662 6 图5 稳定图(b=3.662 6 本文应用Jury判据、分支理论及中心流形投影等理论给出了Logistic中立型差分方程解的稳定性及Flip分支的存在性以及稳定性条件.通过数值模拟验证了所得结论的正确性,并且包含了经典Logistic差分模型的结论(当a2=0时).在对方程参数做了细微的改动后,模型的性状发生了巨大的变化进而出现混沌,可知模型的动力学行为的复杂性. 参 考 文 献: [1] 陈兰荪,宋新宇,路征一.数学生态学模型与研究方法[M].成都:四川科学技术出版社,2008. [2] CUSHING J M.Integrodifferential equations and delay models in population dynamics[M].New York:Springer-Verlag,1977. [3] MURRAY J D.Mathematical Biology[M].New York:Springer-Verlag,1989. [4] OKUBO A.Diffusion and ecological problems:mathematical models[M].New York:Springer-Verlag,1980. [5] WRIGHT E M.A nonlinear difference-differential equation[J].J.Reine Angew.Math,1955 (194):66-87. [6] SMITH F E.Population dynamics in Daphnia magna and a new model for population growth[J].Ecology,1963 (44):651-663. [7] GOPALSAMY K,ZHANG B G.On a neutral logistic equation [J].Dynamics and Stability of Systems,1988 (2):183-195. [8] FREEDMAN H I,Kuang Y.Stability switches in linear scalar neutral delay equations[J].Funkcialaj Ekvacioj,1991 (34):187-209. [9] GOPALSAMY K.Stability and oscillations in delay differential equations of population dynamics[M].Dordrecht:Kluwer Academic Publishers,1992. [10]KUANG Y,On neutral delay two-species Lotka-Volterra competitive systems[J].J.Austral.Math.:Soc.Series B,1991 (32):311-326. [11]KUANG Y.Delay differential equations with applications in population dynamics[M].New York:Academic Press,1993. [12]KUANG Y,FELDSTEIN A.Boundedness of solutions of a nonlinear nonautonomous neutral delay equation[J].Journal of Mathematical Analysis and Applications,1991 (156):293-304. [13]刘敏,陈斯养.具有收获和分段常数变量的捕食-被捕食模型的分支分析[J].云南师范大学学报:自然科学版,2013,33(5):41-47. [14]陈斯养,朱晓琳.具有时滞和分段常数变量的单种群收获模型的分支分析[J].陕西师范大学学报:自然科学版,2013,41(2):1-4. [15]陈斯养,刘晓娜.具有干扰和分段常数变量模型的稳定性及分支[J].山东大学学报:理学版,2012,47(11):109-119. [16]陈斯养,张艳.具有分段常数变量的捕食-被捕食模型的分支分析[J].兰州大学学报:自然科学版,2012,48(3):103-117. [17]张新峰,陈斯养.一类具有时滞的捕食与被捕食模型的稳定性和Hopf分支[J].云南师范大学学报:自然科学版,2012,32(1):36-41. [18]张俊丽,陈斯养.一类具有时滞的广义造血模型的Hopf分支[J].云南师范大学学报:自然科学版,2010,30(1):34-57. [19]李玉红,李海银.一类具有比率依赖密度制约的离散非自治捕食-被捕食系统周期解的存在性[J].云南大学学报:自然科学版,2012,34(5):497-502. [20]王新慧,刘海鸿.具有抑制作用和离散时滞的捕食系统的Hopf分岔分析[J].云南民族大学学报:自然科学版,2012,21(4):286-291 [21]JURY E I.Inners and stability of dynamic systems[M].New York:Wiley,1974. [22]YURI A.Kuznetsov.Elements of applied bifurcation theory[M].New York:Springer-Verlag,1998.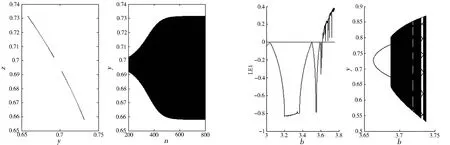
4 结 论

