基于小波域局部二值模式和活动轮廓模型的纹理图像分割*

付明柏

(昭通学院 计算机科学系，云南 昭通 657000)

纹理是一种包含空间上灰度变化和重复的模式，通过纹理人们可以获取非常多的视觉场景信息.二维纹理图像的分析具有非常多的应用，例如：工业表面检测、遥感图像分析、生物图像分析等等.但是，纹理图像的识别、检索、分类和分割具有很多困难，主要原因是在实际中，纹理通常由于方向、尺度或光照条件的变化而变化.另外，同种纹理之中的变化也是一条重要影响因素，这种变化可能使训练样本分布在特征空间的各处，从而导致误分类.

目前，针对纹理分析的这些问题有许多方法，包括灰度共生矩阵(GLCM)方法[1-2]、二维Gabor滤波器组方法[3-4]、局部二值模式(LBP)方法[5-6]等.局部二值模式(LBP)首先由文献[5]提出.LBP是一种将图像变换为整数符号串的算子，这些符号描述图像的局部特征.LBP的基本思想是：纹理在局部上有两个互补的属性，即模式和其强度[5].LBP算子的一个局限是其支撑区域较小.在局部3×3邻域中计算的特征并不能反映纹理在较大尺度上的结构.小波度换方法是进行数字图像处理的有力工具[7-9].文献[10]采用多级双树复合小波(DTCWT)[11]分解纹理图像，得到不同尺度上的图像表达，并用LBP算子对不同尺度的图像表达进行纹理特征提取，得到描述纹理的特征向量.这样在一定程度上克服了LBP支撑区域较小的缺点.

本文采用活动轮廓模型方法[12]对纹理特征向量进行分类.使用活动轮廓模型方法的优点是：(1)无需对特征向量的参数进行估计；(2)使用一定的初始化轮廓曲线可加速算法收敛；(3)由于考虑了上下文信息，分割结果平滑，噪声和孤立区域较少.

1 提出的方法

1.1 双树复合小波(DTCWT)

相对于普通小波，复合小波的主要优点是其平移不变特性和良好的方向选择性.复合小波变换适合于许多图像分析应用，例如图像编码、去噪、检索，等等.滤波器响应的幅值和相位提供了图像在特定尺度和方向上的局部信息和方向特征.

DTCWT由两棵平行实小波树组成.其具有以下优点：(1)近似的位移不变性，即信号的平移不会使小波系数能量发生较大改变；(2)使用方向滤波器进行方向选择，能将图像不同尺度上不同方向的特征进行有效反应；(3)逆变换能够对信号进行完整的重构.

DTCWT可以表示为：

ψ(t)=ψr(t)+jψi(t)

(1)

其中ψr(t)表示复小波的实部，ψi(t)表示复小波的虚部.一维DTCWT的示意图如图1所示.图中，虚线上、下部分分别表示两棵独立的实小波树.h0(n)和h1(n)的输出为DTCWT的实部；g0(n)和g1(n)的输出为DTCWT的虚部.

二维信号进行DTCWT分解时，与离散小波分解类似，即先沿着列再沿着行进行复共轭滤波[13].分解后的信号在第一、二象限各产生3个子带，对应于空间中的6个方向：±15°、±45°、±75°.6个方向子带的滤波器响应如图2所示.其中(a)～(f)子图为实部，(g)～(l)子图为虚部.

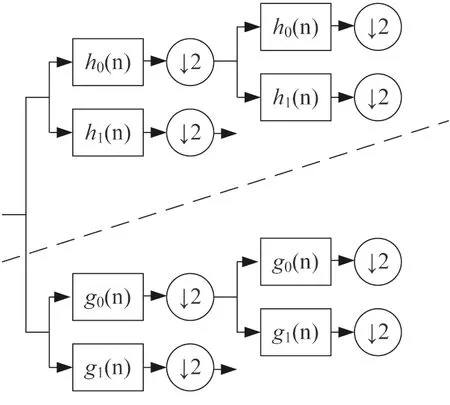
图1 两级1维DTCWT变换

图2 2-D DTCWT滤波器在6个方向上的实部和虚部响应

1.2 局部二值模式(LBP)

Ojala等人于1994年提出了基本LBP算子[5].该算子假设局部纹理具有两种互补属性，即模式和其强度.原始的LBP算子作用于3×3像素邻域块.该邻域块的各个像素以中心像素为阈值二值化.得到的二值序列与2的幂次相乘并相加得到当前中心像素的标号值.由于除去中心像素外邻域块共有8个像素，故总共可获得28=256种不同的标记，取决于邻域像素值减去中心像素值的大小.图3说明了一个3×3像素块的基本LBP算子计算过程.一幅合成纹理图像的LBP图像及直方图如图4所示.

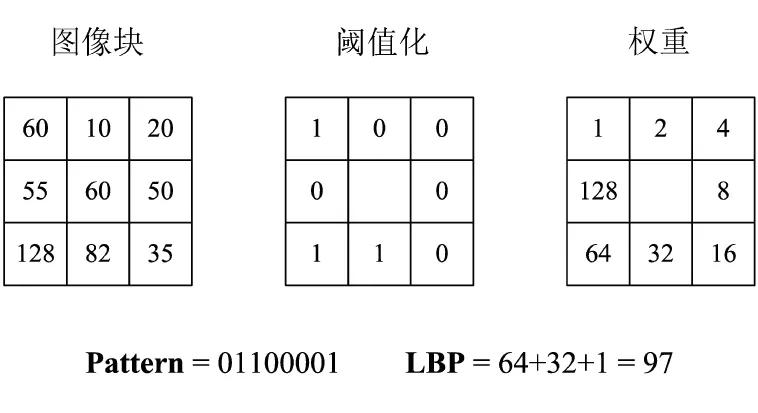
图3 LBP算子计算过程示例

Fig.3 One example of LBP operators processes

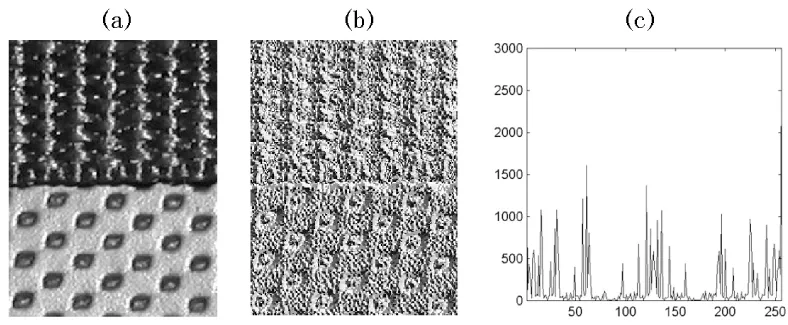
图4 (a)一幅合成纹理图像；(b)LBP图像；

普通LBP算子对于邻域尺寸或者样本点数量没有限制.对于给定图像I，考虑中心为(x,y)，包含P个样本点，半径为R的均匀分布的循环邻域.中心像素和周围邻域像素的灰度值分别为gc和gp.普通LBP算子表示为(2)式，像素和空间关系由(3)式给出[5]，其中s为符号函数.

(2)

(3)

对于特征提取算子，一条期望的属性是旋转不变性.在文献[14]中，基本LBP算子通过旋转不变映射成为旋转不变LBP算子.在这一映射中，所有LBP二值码循环移位成为最小值：

(4)

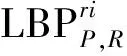
(5)

但文献[14]的分类实验显示该描述子对于输入图像的任意角度旋转具有较强鲁棒性.

1.3 基本活动轮廓模型

活动轮廓模型(ACM)，也称为Snake模型，用于给定初始演化曲线、检测目标边界.为克服原始Snake模型依赖于边缘的缺点，Chan和Vese在文献[15]和[16]中提出了C-V模型.该模型假定图像前景和背景具有各自的灰度均值，并且两部分灰度值近似为常数.在这一假设下，C-V模型最小化以下泛函[15]：

(6)

其中c1、c2分别是前景和背景的平均灰度.C是演化曲线.μ、λ1和λ2是各个能量项的权重参数.

对于彩色图像，C-V模型具有向量值形式[16]：

(7)

其中N为图像通道数，i为通道索引.

1.4 LBP引导的ACM(LAC)

文献[12]中使用LBP引导的ACM，即LAC进行了纹理图像的分割.但LBP具有支撑区域较小这一缺点.本文使用DTCWT域的LAC进行纹理图像分割，以克服LBP支撑区域小这一缺点.具体方法如下：

(1)DTCWT分解，对于分辨率小于原始图像分辨率的子带，使用上采样还原分辨率.

(2)子带的特征提取：

(8)

条件熵Hi可用于描述给定LBP值i的纹理判别能力.如果像素集中在某些块上，则Hi较小，因此较小的Hi值意味着对应的LBP值i在图像区域上占主要地位.

(3)累积二值图像的生成；

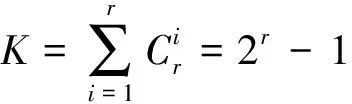
(4)使用ACM分割；

使用向量值无边缘活动轮廓模型进行分割.使用文献[12]中的能量函数，并考虑不同尺度和方向子带，得到改进的能量泛函：

(9)

其中，C是演化曲线，c+、c-分别为演化曲线C内外部分的平均值.u是平滑后的累积二值图像CB在不同尺度和方向上的像素值.i、j分别为尺度和方向索引号.L、D分别为最大尺度和方向数，对于DTCWT，D=6；本文取分解级数为3，即L=3.使用水平集方法，以上能量泛函的欧拉-拉格朗日方程为：

(10)

其中，φ是水平集嵌入函数，δ(t)是正则化Heaviside函数的导数，u是曲线长度项权重.

2 总体算法

本文提出的方法首先使用DTCWT分解纹理图像，然后使用LBP对各个尺度和方向子带提取纹理特征，利用最大熵原则对所得特征图像进行选择以得到具有最大纹理区分能力的特征图像.向量值ACM用于最后的分割.算法总体流程如图5所示.算法伪代码如下：

(1)DTCWT分解

(2)计算LBP值

For 每个尺度，每个方向，每个像素(x,y)，计算LBP值；End

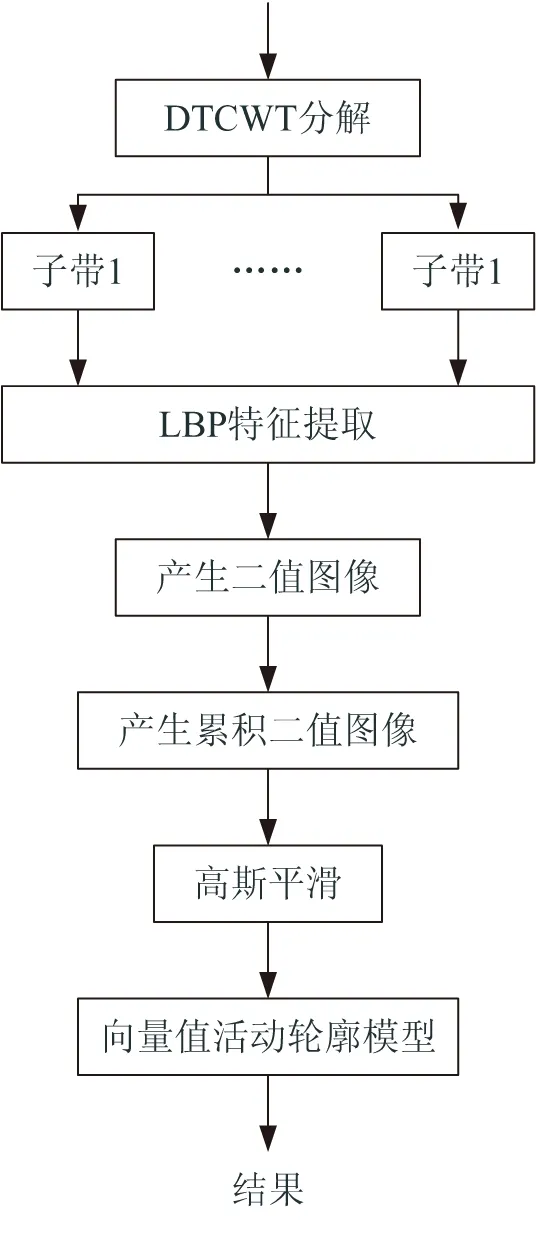
图5 算法流程图

(3)产生二值图像Bi

初始化Bi(x,y)=0；

(4)产生累积二值图像CB

根据条件熵排列二值图像Bi；

选择前r幅二值图像B1～r；

For前r幅二值图像的每种非空组合COMBk={Bi1,…Bil}，

doCBk=Bi1,∧…∧Bil; End (其中∧表示OR操作)

(5)平滑并使用向量值无边缘活动轮廓模型分割累积二值图像CB.

3 实验结果及讨论

3.1 实验设计

为评价提出的纹理图像分割算法，使用Brodatz图像数据集[17]和VisTex图像数据集[18]进行了纹理分割实验.每幅Brodatz图像的大小为256×256像素；而每幅VisTex图像的大小为512×512像素.对于Brodatz数据集，实验使用的合成纹理图像由数据集中不同种类的纹理经过拼接得到.对于VisTex数据集，直接选择其中包含纹理的自然场景图像，并丢弃颜色信息，仅保留灰度值信息.两个数据集的输入图像如图6、7所示.算法使用MATLAB 7实现，实验硬件平台为Intel(R) Core2(TM) 2.1 GHz CPU，3 GB内存.实验结果采用分类误差率衡量，其计算公式为：

3.2 Brodatz数据集实验结果

本算法对于Brodatz数据集的实验结果如图8所示.定量结果如表1所示，其中包含与文献[5]和[9]的比较.由图7和表1可见，本算法对于合成纹理图像的分割精度较高.边缘定位较为精确，噪声和误分类较少.其中最小误差率达到0.31%.对于最相近的合成纹理图像，即图5(i)所示的图像，分割误差率也达到1.62%.

3.3 VisTex数据集实验结果

本算法对于VisTex数据集的实验结果如图9所示.由于自然场景图像的分割不具有确定客观标准，故没有给出定量分割精度，只能通过主观评价分割效果.由图9可见，本算法对于含有不同纹理的自然图像能够基本准确的分割出背景和前景.前景目标边缘光滑，噪声和孤立区域较少，基本符合图像主观理解.

3.4 讨论

由3.2节和3.3节实验结果可见，本算法对于合成纹理图像和自然场景图像有较高的分割精度.其中对于Brodatz数据集的合成纹理图像，大多数图像的分割精度优于文献[5]和[12].这是由于本算法相比于文献[5]和[12]中的算法，考虑了DTCWT域的不同尺度和方向上的信息，并且扩大了LBP算子的支撑区域.值得注意的是，对于图8(i)所示的图像，本算法的分割精度低于其他方法.这是由于，虽然本方法扩大了LBP算子的支撑区域，但图8(i)图像中的两种纹理十分相近，也就是说这两种纹理的边缘十分模糊.在DTCWT的较高尺度上，这样的模糊边缘被再次模糊.故本方法对于该图像的分割结果中出现了边缘定位偏差较大的现象，导致错误率上升.

4 结论

本文提出了一种基于双树复小波(DTCWT)域局部二值模式(LBP)和活动轮廓模型(ACM)的纹理图像分割方法.该方法在DTCWT域下对不同尺度和方向子带上的图像利用LBP算子进行特征提取，并利用最大熵原则对所得特征图像进行选择以得到具有最大纹理区分能力的特征图像.最后使用向量值无边缘活动轮廓模型进行分割.演化曲线最后收敛于不同种类纹理的边界.实验结果表明，本方法能够较好的对Brodatz合成纹理图像和含有纹理的VisTex自然场景图像进行分割.其中，本方法对于大多数Brodatz合成纹理图像的分割误差率均小于1%，与其他主流方法的精度相当.

图6 Brodatz数据集的合成纹理图像

Fig.6 Brodatz data sets synthesis texture images

图7 VisTex数据集的自然场景图像

Fig.7 VisTex data sets nature scenes images

图8 Brodatz数据集的实验结果

图9 VisTex数据集的实验结果

表1 Brodatz数据集的分类误差率(%)

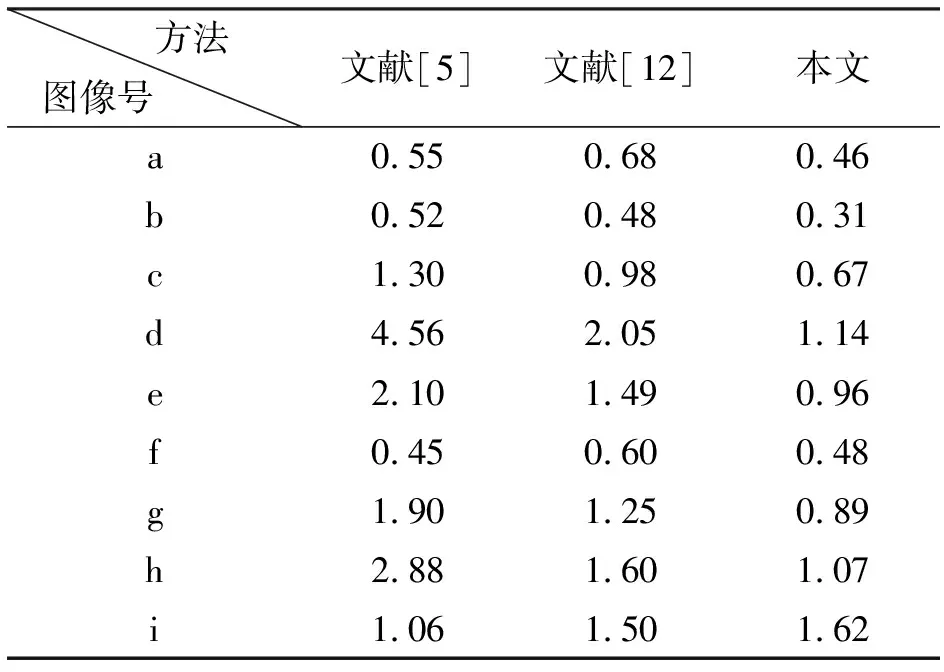
Table.1 Classification error rate of the Brodatz data sets

参 考 文 献:

[1] JIA L,ZHOU Z,LI B.Study of SAR image texture feature extraction based on GLCM in Guizhou Karst mountainous region[C].2nd International Conference on Remote Sensing,Environment and Transportation Engineering(RSETE),Nanjing,China,2012:1-4.

[2] 潘赢.基于双树复小波和灰度共生矩阵的遥感图像分割[D].大连：辽宁师范大学，2011.

[3] 柯维.基于灰度共生矩阵和BP神经网络的织物组织结构识别[D].苏州：苏州大学，2011.

[4] WANG S,XIA Y,LIU Q,et al.Gabor feature based nonlocal means filter for textured image denoising[J].J.Vis.Commun.Image Represent,2012,23(7):1008-1018.

[5] OJALA T,PIETIKAAINEN M,HARWOOD D.Performanceevaluation of texture measures with classification based on Kullback discrimination of distributions[C].Proceedings of the 12thIAPR International Conference on Pattern Recognition,Jerusalem,1994 (1):582-585.

[6] 张虎，方贤勇，吴忠标.基于多尺度细胞局部二值模式的人体检测[J].计算机技术与发展，2012，22(7)：52-56.

[7] 尹慧平，蔡维维，李博. 基于分数阶混沌和分数阶混沌小波变换的数字指纹技术[J]. 云南民族大学学报：自然科学版，2013，22(3)：217-221.

[8] 卢维娜，王亚玲，周小辉. 在Matlab下平衡多小波cardbal4对数字水印的新方法[J]. 新疆师范大学学报：自然科学版，2013,32(1):26-32.

[9] 吐尔洪江·阿布都克力木，阿布都许库热·阿布都克力木，艾热提·阿不力克木. 基于二进小波变换的图像阈值滤波法的性能分析[J]. 新疆师范大学学报：自然科学版，2013,32(2):1-6.

[10]WANG Y X,RUAN Q Q,PAN X.Palmprint recognition method using dual-tree complex wavelet and transform and local binary pattern histogram[C].International Symposium on ISPACS,Xiamen,China,2007:646-649.

[11]VO A,ORAINTARA S.A study of relative phase in complex wavelet domain:Property,statistics and applications in texture image retrieval and segmentation[J].Signal Processing:Image Communication,2010,25(1):28-46.

[12]SAVELONASM A,IAKOVIDIS D K,MAROULIS D.LBP-guided active contours[J].Pattern.Recogn.Lett.2008,9(1):1404-1415.

[13]田立伟.复小波框架、M尺度复小波及对偶树复小波的构造[D].西安：陕西师范大学，2011.

[14]宋翠玉，李培军，杨锋杰.基于多元局部二值模式的遥感图像纹理提取与分类[J].遥感技术与应用，2011，26(3)：322-327.

[15]CHAN T F,VESE L A.Active contours without edges[J].IEEE Transaction on Image and Processing.2001,10(2):266-277.

[16]CHAN T F,SANDBERG B Y,VESE L A.Active contours without edges for vector-valued images[J].J.Visual Comm.Image Rep.,2000,11(2):130-141.

[17]Brodatztextures[OL].http://www.ux.uis.no/～tranden/brodatz.html

[18]MIT Vision and Modeling Group.Vision Texture[OL].http://vismod.www.media.mit.edu