滑模/无模型自适应控制方法及在离心-振动试验系统中的应用

王跃钢，左朝阳,，郭志斌，文超斌

（1.第二炮兵工程大学 自动控制系，西安 710025；2.中国人民解放军96165部队，上饶 334109）

滑模/无模型自适应控制方法及在离心-振动试验系统中的应用

王跃钢1，左朝阳1,2，郭志斌1，文超斌1

（1.第二炮兵工程大学 自动控制系，西安 710025；2.中国人民解放军96165部队，上饶 334109）

针对滑模控制对非匹配不确定性系统的控制问题，提出了滑模/无模型自适应控制算法。通过滑模控制方法对系统的标称部分及匹配部分进行控制，对于非匹配不确定性部分，以滑模控制器的输出与系统期望输出的误差作为无模型自适应控制器的输入，通过无模型自适应方法来减少未建模不确定性对系统控制的影响。该方法对系统中匹配和非匹配不确定项均具有鲁棒性,比传统滑模控制及无模型自适应方法具有更快的收敛速度。理论分析证明了系统的稳定性,仿真结果验证了该方法的有效性。

滑模控制；自适应；无模型；试验系统

通常惯性器件误差模型的建立，对于飞行器上精确控制的惯导系统的制导效果起着关键作用，为此，精确地建立惯性器件的误差模型显得非常重要，而对惯性器件误差模型的建立需要一种非常真实的空中环境。目前国内外一般通过复合离心机-振动台试验系统模拟惯性器件所处的过载-振动复杂环境，但离心-振动试验系统的实验研究的进展仍有很大阻力，除了受实验设备本身的限制之外，控制方法的研究也存在很大困难。

由文献[1]针对顺臂安装的复合离心-振动试验系统建立的动力学模型可知，离心力-振动试验系统因离心机与振动台之间运动存在耦合现象而成为一种不确定非线性系统，而在实际系统中，系统的参数经常是未知的，建模时需对其进行必要的简化，然而在简化过程中，势必不可避免地存在未被建模的动态不确定，这些未建模环节的动态特性可能对系统产生很大的影响。而滑模控制是处理系统中不确定性的有效方法之一，当不确定性满足匹配条件时，滑模控制具有“不变性”[2]，其控制器设计简单，鲁棒性强，在电机、机械臂、飞行器、混沌系统等不确定非线性系统控制中得到广泛应用[3-6]。而对于非匹配不确定性，滑模控制则不再具有“不变性”，丧失了强鲁棒性，这种情况下传统的滑模控制方法不能取得优化的控制性能指标。近几年发展起来的无模型自适应控制（Model free Adaptive Control，MFAC）思想是一种基于数据驱动的递推设计方法，将伪偏导数估计算法和控制器设计结合在一起，控制器设计仅需要被控系统的量测 I/O数据，无需任何模型信息，无需训练过程，在线调整参数较少，是一种低成本的控制器[7-9]。

将该方法引入非匹配不确定系统与未建模系统中，结合滑模控制理论设计了滑模/无模型自适应控制方法，来克服现有滑模控制方法的不足。由于实际工程中采样的数据都是离散的，本文采用了离散滑模控制方法。并将此方法应用于离心-振动试验系统的振动控制系统中，仿真实验结果表明滑模/无模型自适应控制具有较好的控制性能，能够满足系统跟踪控制，跟踪误差精度得到了有效提高。

1 离散滑模控制器设计

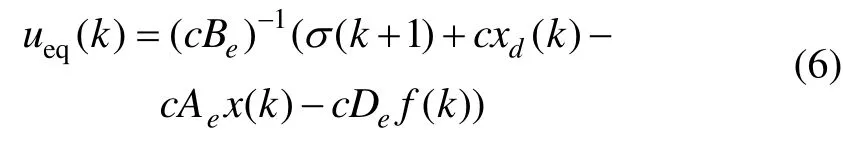
本文利用一种快速趋近律的方法来解决系统快速收敛的问题，同时可以减弱系统抖振，该方法能够快速单调的向切换面趋近，并在有限步到达切换面。因此采用快速幂次趋近律[10]设计离散滑模控制器，其趋近律表示为：

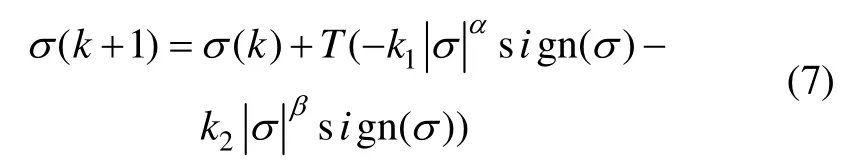
式中，α＞1，0＜β＜1，k1＞0，k2＞0。当系统运动点远离切换面时，上式中第一项将起到主要作用；当系统运动点接近切换面时，第二项起主要作用，两项结合以保证系统运动在整个状态空间具有良好的运动品质。那么系统的控制律将表示为：

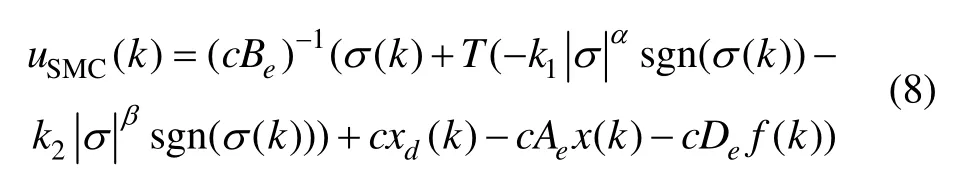
2 无模型自适应控制方法

无模型自适应控制方法是韩志刚、侯忠生等人于1994年提出的，它是数据驱动控制领域的一种比较前沿的控制理论与技术。其设计过程对受控对象的数学模型不作要求，不需要更多的辨识对象，可通过系统稳定性分析确保系统的闭环稳定。

假设一般的离散时间系统如下：

式中，u(k)∈R、y(k)∈R分别表示k时刻系统的输入和输出，m n、分别为系统未知的输出与输入阶数，为未知非线性时变函数。

对于以上系统可做如下假设：

假设1：系统(9)是输入输出客观可控的，即对于一个系统有界的期望输出信号，必然有一个有界的控制输入型号，能够使系统在此输入下其输出等于系统的期望输出。

假设 2：f(·)关于系统当前的控制输入信号u(k)的偏导数是连续的。

假设 3：系统(10)是广义 Lipschitz的，即对任意k和，其中，，λ是常数。

对于以上假设的条件相对比较宽松，大部分非线性系统都能够满足，因此它是合理的，于是有：

引理 1[7]：对于一般离散时间系统(9)，满足以上假设条件1～3，当时，一定存在一个被称为伪偏导数的量φ(k)，使得非线性离散系统动态线性化为：

具体证明见文献[5]。

对于式(10)中的伪偏导数φ(k)在非线性系统中是一个时变参数，如果将采样周期取得较小且控制输入变化不大，对φ(k)可通过参数估计的方法进行估计。为此，本系统采用文献[9]的估计方法：

现有的控制律算法由以下给出的准则函数得出：

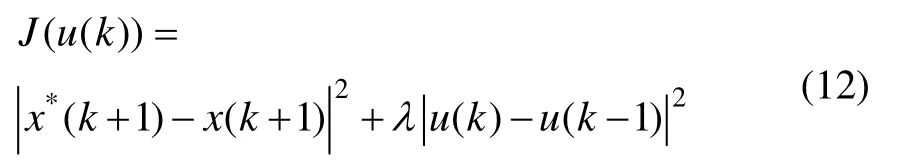
将式(9)代入式(12)，然后对u(k)求导，令其等于零，得出：

算法的稳定性分析可见文献[10]。

从以上伪偏导数估计算法和控制律可以看出，无模型自适应控制基于伪偏导数等新概念,它是一种基于输入输出增量形式的，仅使用受控系统的I/O数据，具有结构简单、可调参数适中、方便控制器设计、方便输入输出数据的直接利用等特点。

3 系统控制器设计

对于一个非匹配不确定系统，系统中包括两个部分确定性部分和不确定性部分，其中，不确定性部分主要由外部扰动、系统的质量、刚度、阻尼等引起的。

定义实际系统由两个部分形成：确定性部分和非匹配不确定性部分，以下是非匹配不确定系统数学模型。将滑模控制与无模型控制相结合对非匹配不确定系统进行混合控制，滑模控制对于匹配的标称系统进行控制，以滑模控制输出与期望输出的误差作为无模型控制的输入。具体形式如下：

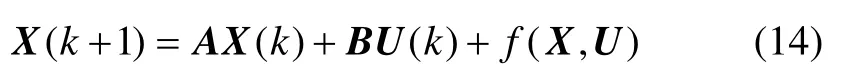
式中，f(X,U)表示系统的不确定性部分，即未建模部分。整个控制系统的结构如图1所示，图中xd为期望输出值。

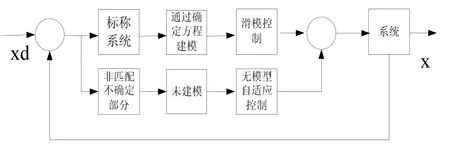
图1 控制系统结构图Fig.1 Block diagram of control system

以上第1、2两节分别对其各自控制率稳定性进行了证明。当误差率差值超过一定值时，MFAC表现为较强的控制作用，且输出逐步增大，误差小时增长率小，误差大时增长率大；反之，MFAC表现为较弱的控制作用。

定理 1：对于离散系统(2)，在控制律(15)的作用下，将保证系统是稳定和收敛的。

稳定性证明：

定义正定函数

而

因为

同时当采样时间T非常小时，满足

4 仿真研究

4.1 离心-振动试验系统

离心力-振动复合环境模拟试验系统可简化为中心刚体-旋转梁-振动台物理模型，如图2所示。为简化系统模型，做以下三点假设：1）电动振动台只有一个自由度；2）气隙磁通密度为常数；3）电动振动台等效为一个刚体。则振动台的动力学模型可如下表示[11]：

再根据多刚体动力学方程，在离心力作用下振动台面所受广义力为：

将以上离心-振动试验系统动力学模型描写成状态方程为：

可写为以下形式：

以上公式中，x、v分别为振动台面的位移和速度；B为励磁线圈磁感应强度；i为线圈电流；l为动圈线圈的总长度；r为动圈质心到离心机转轴的水平距离；k0为刚度系数；c为阻尼系数；ω为离心机转速；m动圈等效质量。由于离心机转速ω的变化，使得系统参数具有时变性和不确定性。

图2 离心力-振动试验系统物理模型Fig.2 Physics model of centrifuge force-vibration test system

将以上系统转换成离散系统，设样本时间为Td，在样本时间内控制力维持不变,具体如下：

连续系统结果可以转换成离散系统结果为:

式(25)进一步简化为：

4.2 系统仿真

将第3节控制方案用于以上系统中，来验证本文提出的滑模/无模型自适应方法的正确性和有效性。选取如下离心振动复合系统参数进行数学仿真。台面、动圈等效质量m=1.5 kg；刚度k0=9500 N/m；阻尼c=50 N/(ms-1)；磁感应强度B=0.5T；动圈长度l=28 m；电阻R=0.5 Ω；磁感L=100 μH；初始位移x0=0，速度v0=0，电流i0=0；r=1.5 m；干扰力为d=10sin(2πt/16)；ε=0.005；ω=π/6 rad/s。滑模控制中参数设为k1=0.7，k2=2，α=1.5，β=0.5。无模型自适应算法式(11)(13)中选取ρ=0.6，η=1，γ=0.1；ε设置为10-5。

一般飞行器在飞行过程中所受振动的频率与幅值不可能是固定的，为了反映更为真实的振动环境，对最大振幅为0.08，频率可发生变化的振动情况进行了仿真。仿真结果如图3、图4所示。可以看出，在复杂振动情况下，系统仍然能够很快跟踪指令信号，并达到很高的跟踪精度,证明了本文算法的有效性。

为了进一步体现本文算法的优越性，图5、图6分别给出了在输入正弦指令下，干扰力d=10sin(2πt/16)，以及由ω引起不确定性Δk=0.02k，Δc=0.03c，本文算法与传统滑模控制及无模型自适应方法的响应曲线比较。

从图5、图6仿真结果能够看出，系统的实际输出能够较好地跟踪参考输入，且比单一的滑模控制及无模型自适应控制收敛速度快、精度高，系统的鲁棒性和抗干扰性更强。从而证明了本文算法具有一定实用性。

图3 复杂轨迹响应曲线Fig.3 Complex trajectory response curve

图4 复杂振动跟踪误差曲线Fig.4 The curve of complex trajectory tracking error

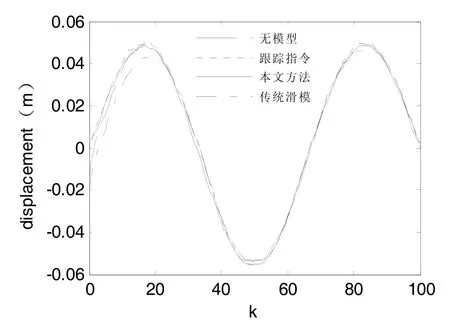
图5 正弦函数跟踪曲线Fig.5 sine wave response trace curve

图6 正弦函数跟踪误差曲线Fig.6 Sine wave response trace error curve

5 结 论

本文针对非匹配不确定系统，介绍了一种滑模/无模型自适应控制方法，该方法在对非线性不确定系统进行控制过程中,通过滑模控制方法对系统标称部分进行控制，然后将滑模控制输出值与给定值之差作为未建模不确定性部分的输入值，输入到无模型自适应控制器中，通过系统的在线I/O数据,对未建模不确定性部分进行控制,并给出了该控制方法的稳定性证明。然后将此控制方法应用在离心-振动试验系统中，仿真结果验证了所提方案的有效性，并通过与单一的滑模控制相比，系统的收敛速度和精度都得到了提高，对模拟惯性仪器的动态环境具有一定的参考价值。

（References）：

[1]朱先辉，闰桂荣，牛宝良，李荣林.离心力场中电动振动台的建模[J].振动与冲击，1999，18(3)：37-44.ZHU Xian-hui,YAN Gui-rong,NIU Bao-liang,LI Rong- lin.Modelling of electrodynamic vibrator under centrifugal force field[J].Journal of Vibration and Shock,1999,18(3): 37-44.

[2]Hung J Y,Gao W B,Hung J C.Variable structure control:A survey[J].IEEE Transaction on Industrial Electronics,1993,40(1): 2-22.

[3]王家军.基于自回归小波神经网络的感应电动机滑模反推控制[J].自动化学报，2009，35(1)：1-10.WANG Jia-Jun,Sliding mode backstepping control of induction Motor Based on self-recurrent wavelet neural networks[J].Acta Automatica Sinica,2009,35(1): 1-10.

[4]刘姝阳，刘克平，李元春.基于耦合滑模面的机械臂操作柔性负载系统分布参数控制[J].吉林大学学报，2013，43(1)：267-273.LIU Shu-yang,LIU Ke-ping,LI Yuan-chun.Distributed parameter control for system of manipulator handling a flexible payload based on coupled sliding surface[J].Journal of Jilin University.2013,43(1): 267-273.

[5]Godard D,Kumar K D.Fault tolerant reconfigurable satellite formations using adaptive variable structure techniques[J].Journal of Guidance,Control and Dynamics,2010,33(3): 969-984.

[6]Moez F.Sliding mode control and synchronization of chaotic systems with parametric uncertainties[J].Chaos,Solitons & Fractals,2009,41(3): 1390-1440.

[7]Hou Zhongsheng,Bu Xuhui.Model free adaptive control with data dropouts[J].Expert Systems with Applications,2011,38: 10710-10717

[8]Hou Zhongsheng,Jin Shangtai.Data-driven model-free adaptive control for a class of MIMO nonlinear discretetime systems[J].IEEE Transaction on Neural Networks,2011,22(12): 2173-2186.

[9]Bu Xuhui,Yu Fashan,Hou Zhongsheng,et al.Model-free adaptive control algorithm with data dropout compensation[J].Mathematical Problems in Engineering,2012,55: 1-14.

[10]张合新，范金锁，孟飞，黄金峰.一种新型滑模控制双幂次趋近律[J].控制与决策，2013，28(2)：289-294.ZHANG He-xin,FAN Jin-suo,MENG Fei,HUANG Jin-feng.A new double power reaching law for sliding mode control[J].Control and Decision,2013,28(2): 289-294.

[1]郭继峰，任万滨，康云志，等.电动振动台模型辨识方法及其应用的研究[J].振动与冲击，2011，30(7)：241-244.GUO Ji-feng,REN Wan-bin,KANG Yun-zhi,et al.Model identification method for a electrodynamic vibration shaker and its application[J].Journal of vibration and shock,2011,30(7): 241-244.

Application of slide mode/model-free method in centrifuge-vibration test system

WANG Yue-gang1,ZUO Zhao-yang1,2,GUO Zhi-bin1,WEN Chao-bing1
(1.Department of Automatic Control Engineering,the Second Artillery Engineering University,Xi’an710025,China;2.Unit 96165 of the Chinese People’s Liberation Army,Shangrao 334109,China)

In view of the sliding mode control problem in the uncertain system with unmatched time-varing uncertainties,an adaptive control algorithm based on sliding model/model-free method is proposed.The nominal system is controlled by slide mode controller in the uncertain system.In order to reduce the influence of unmatched uncertainties,the error caused by the output of the slide model and the system expected output is taken as the control input of the model free method.The motor speed of this control method can reach the given value more rapidly than that of a general slide-mode control and model-free method.Mathematics and the simulation results prove the good system stability and the effectiveness of this algorithm.

slide mode control; adaptive; model free; test system

U666.1

：A

1005-6734(2014)02-0276-05

10.13695/j.cnki.12-1222/o3.2014.02.025

2013-11-25；

：2014-03-27

国防预研（2001D1302）

王跃钢（1958—），男，教授，博士生导师，从事导航与制导技术研究。E-mail：wangyueg@163.com