图ω4g,4h+3的（r1,r2,…,r4g,4h+2）-冠的优美性

张政，胡红亮

（西安航空学院理学院，陕西西安710077）

图ω4g,4h+3的（r1,r2,…,r4g,4h+2）-冠的优美性

张政，胡红亮

（西安航空学院理学院，陕西西安710077）

给出了ω4g,4h+3的（r1,r2,…,r4g,4h+2）-冠的定义，讨论了ω4g,4h+3的（r1,r2,…,r4g,4h+2）-冠的优美性，用构造性的方法给出了一些特殊的ω4g,4h+3的（r1,r2,…,r4g,4h+2）-冠的优美标号。证明了一些特殊的ω4g,4h+3的（r1,r2,…,r4g,4h+2）-冠是交错图。

圈；冠；优美图；交错图

1 引言与概念

优美图是图论中极有趣的研究课题，有着较好的应用价值和广阔的研究前景。它的研究是从1963年GRingel提出的一个猜想和1966年A Rosa的一篇论文开始的。1972年，SW Golomb明确给出了优美图的定义。近几十年，国内外获得不少关于优美图的研究成果，它们被应用于射电天文学，X-射线衍射晶体学，密码设计，通信网络编址，导弹控制码设计，同步机码设计等领域。

文中所讨论的图均为无向简单图，V(G)和E(G)分别表示图G的顶点集和边集，未说明的符号及术语均见文［1］。

定义1［1］对于一个简单图G=V(G),E(G)=(V,E)，如果对每一个顶点v∈V，存在一个非负整数θ(v)（称为顶点v的标号）使满足：

①∀u,v∈V，若u≠v，则θ(u)≠θ(v)。②max{θ(v)|v∈V}=|E|。③∀e1,e2∈E，若e1≠e2，则θ'(e1)≠θ'(e2)。其中：θ'(e)=|θ(u)-θ(v)|，e=uv（称θ'(e)为边e的标号），则G称为优美图，θ(v)称为G的一个优美标号。

定义2［1］在图G每个顶点都粘接了r条悬挂边（r≥1的整数）所得到的图，称为图G的r-冠，图G的1-冠，称作图G的冠。

定义3V(G)={v1,v2,...,vn}的每个顶点vi都粘接了ri条悬挂边（ri≥0的整数，i=1,2,...,n）所得到的图，称为图G的(r1,r2,...,rn)-冠，简记为G(r1,r2,...,rn)。特别地，当r1=r2=...=rn=r时，称为图G的r-冠。图G的0-冠就是图G。

定义4［1］由圈Cm和Cn恰有一个公共点所组成的图记为图ωm,n。

定义5［2］G是一个优美二部图，其优美标号为θ，V(G)划分成两个集合X,Y，如果maxθ(v)＜minθ(v)，则称θ是G的交错标号，称G是在交错标号θ下的交错图。

文献［1］中证明了P1∨Pn及其r-冠是优美的，从而猜测：任意优美图的r-冠都是优美的，在此猜想的指导下，文献［3-5］中证明了：当n≡0,3(mod4)时，图Cn及其r-冠是优美图；文献［6-8］中给出了图Cn的(r1,r2,...,rn)-冠的定义，讨论了n=3,7,8,11,4h,4h+3时，图Cn的(r1,r2,...,rn)-冠的优美性；文献［10-12］给出了ωm,n的(r1,r2,...,rm+n-1)-冠的定义，讨论了(m,n)=(4,4),(4,6),(5,6),(5,7)时，图ωm,n的(r1,r2,...,rm+n-1)-冠的优美性。本文证明了图ω4g,4h+3的(r1,r2,...,r4g+4h+2)-冠的优美性，并给出了4种不同的优美标号，同时证明了这些优美标号也是交错标号。

2 主要结果及其证明

定理当m=4g，n=4h+3，g和h为任意自然数，ri为任意非负整数（i=1,2,...,m+n-1），图ωm,n的(r1,r2,...,rm+n-1)-冠的顶点集如图1所示，V(ωm,n)=(v1,v2,...,vm,vm+1,...,vm+n-1)，与vi邻接的悬挂边（或叶）记为xij（vi∈V(ωm,n)，j=1,2,...,ri），当时，ωm,n的(r1,r2,...,rm+n-1)-冠是优美图且为交错图。

图1 ω4g,4h+3的(r1,r2,...,r4g+4h+2)-冠Fig.1 The(r1,r2,...,r4g+4h+2)-corona of the graphω4g,4h+3

第1种优美（交错）标号：

容易验证：

θ:V（ω4g,4h+3的() r1,r2,...,r4g+4h+2-冠）→是一个单射。

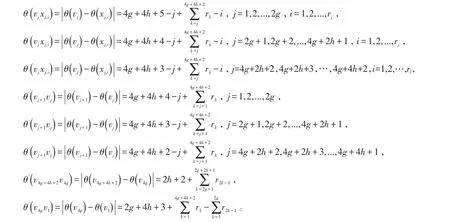
因此，θ是ω4g,4h+3的(r1,r2,...,r4g+4h+2)-冠的交错标号。即ω4g,4h+3的(r1,r2,...,r4g+4h+2)-冠是交错图。第2种优美（交错）标号：

第3种优美（交错）标号：

第4种优美（交错）标号：

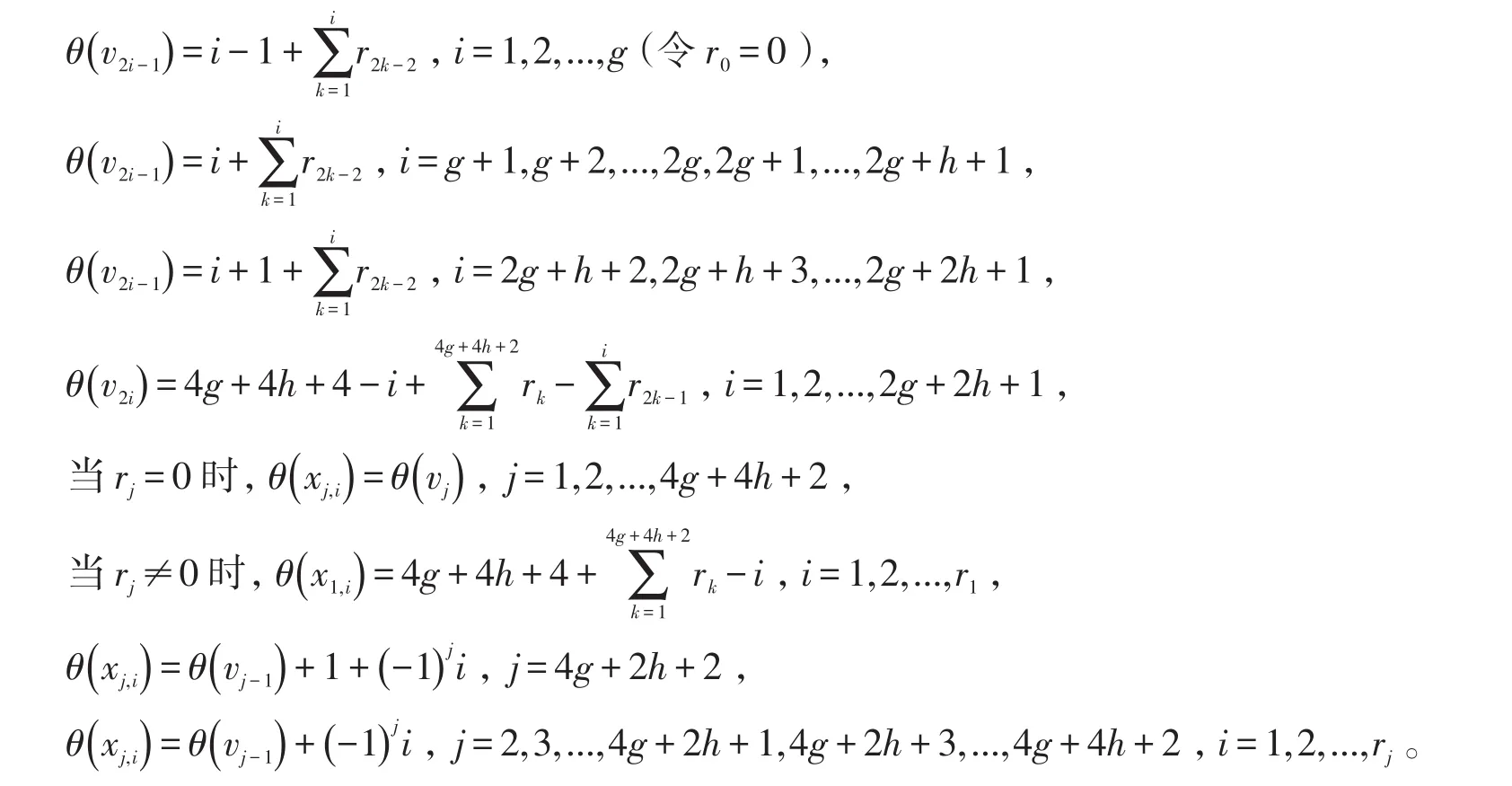
第2、3、4种优美交错标号的证明类似于第1种优美交错标号，此处略。

例下面根据定理给出ω8,11的(1,2,3,2,3,1,1,2,2,1,3,2,1,2,1,2,3,2)-冠的4种交错标号，如图2～图5所示。

图2 图ω8,11的(1,2,3,2,3,1,1,2,2,1,3,2,1,2,1,2,3,2) -冠的第1种交错标号Fig.2 The firstalternating labeling of the (1,2,3,2,3,1,1,2,2,1,3,2,1,2,1,2,3,2) -corona of the graphω8,11

图3 图ω8,11的(1,2,3,2,3,1,1,2,2,1,3,2,1,2,1,2,3,2) -冠的第2种交错标号Fig.3 The second alternating labeling of the (1,2,3,2,3,1,1,2,2,1,3,2,1,2,1,2,3,2) -corona of the graphω8,11

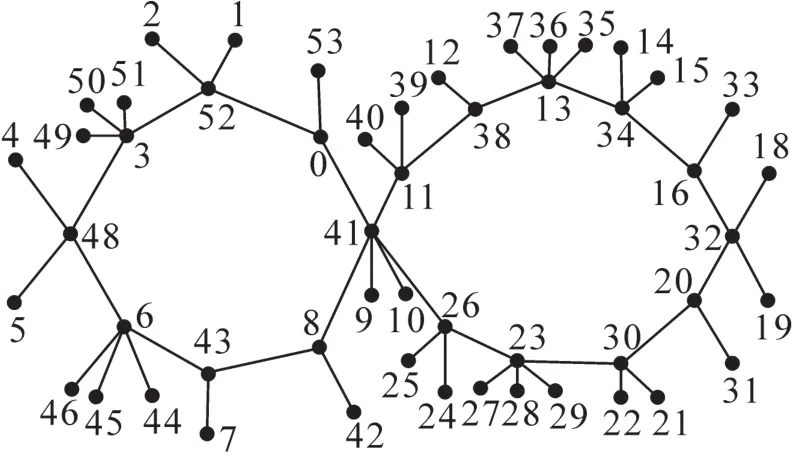
图4 图ω8,11的(1,2,3,2,3,1,1,2,2,1,3,2,1,2,1,2,3,2)-冠的第3种交错标号Fig.4 The third alternating labeling of the(1,2,3,2, 3,1,1,2,2,1,3,2,1,2,1,2,3,2)-corona of the graphω8,11

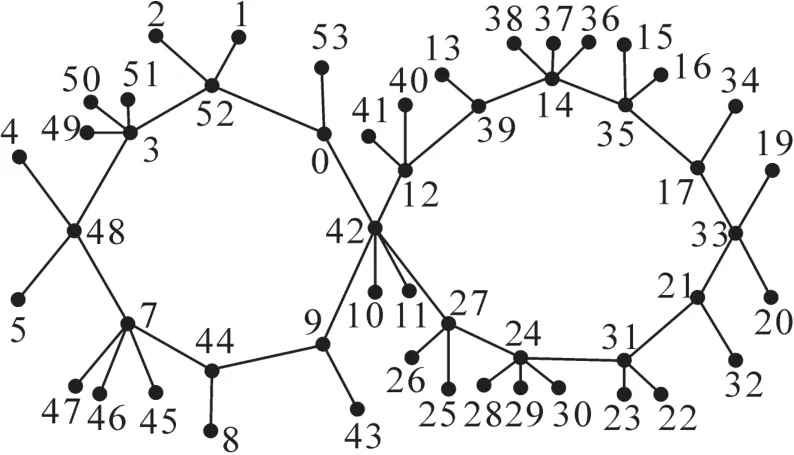
图5 图ω8,11的(1,2,3,2,3,1,1,2,2,1,3,2,1,2,1,2,3,2)-冠的第4种交错标号Fig.5 The fourth alternating labeling of the(1,2,3,2, 3,1,1,2,2,1,3,2,1,2,1,2,3,2)-corona of the graphω8,11

[1]马克杰.优美图[M].北京:北京大学出版社,1991:10-15.

[2]杨显文,张志尚.一类交r错图并的优美性[J].吉林工程技术师范学院学报:自然科学版,2007,23(6):8-10.

[3]武建春.图D2,4k与它的-冠的优美性[J].内蒙古电大学刊,2002(1):34.

[4]曾朝英,武建春.关于优美图Cn和r¤k1的r-冠的优美性[J].集宁师专学报2000,22(4):4-7.

[5]胡红亮.图Cn的r-冠的新的优美标号[J].纯粹数学与应用数学[J].2010,26(3):454-457.

[6]吴跃生,李咏秋.关于圈Cn的(r1,r2,...,rn)-冠(n=7,8)的优美性[J].阜阳师范学院学报:自然科学版,2010,27(3):20-23.

[7]吴跃生,李咏秋.再探圈Cn的(r1,r2,...,rn)-冠(n=7,8)的优美性[J].阜阳师范学院学报:自然科学版,2010,27(4):1-4.

[8]吴跃生.关于圈C4h的(r1,r2,...,r4h)-冠的优美性[J].华东交通大学学报,2011,28(1):77-80.

[9]曾朝英.图ω4k,n的r-冠的优美性[J].集宁师专学报,2001,23(4):4-6.

[10]吴跃生,李咏秋.关于图ω4,4的(r1,r2,...,r7)-冠的优美性[J].宜春学院学报,2010,32(12):1-3.

[11]吴跃生.关于图ω4,6的(r1,r2,...,r9)-冠的优美性[J].宜春学院学报,2011,33(8):1-3.

[12]吴跃生,李咏秋.关于图ω5,6的(r1,r2,...,r10)-冠的优美性[J].北京联合大学学报,2011,25(2):60-61.

[13]吴跃生,李咏秋.关于图ω5,7的(r1,r2,...,r11)-冠的优美性[J].嘉应学院学报,2011,29(5):5-8.

[14]吴跃生,王广富,徐保根.关于图C4h+1⊙k1的(Gr1,Gr2,Gr3,...,Gr4h+2)-冠的优美性[J].山东大学学报:理学版,2013,48(4):25-28.

On the Gracefulnessof the() r1,r2,...,r4g+4h+2-corona of the Graphω4g,4h+3

Zhang Zheng,Hu Hongliang
(Schoolof Science,Xi’an AeronauticalUniversity,Xi’an 710077,China)

A definition hasbeen given for the(r1,r2,...,r4g+4h+2) -corona of the graphω4g,4h+3.The gracefulnessof the (r1,r2,...,r4g+4h+2) -corona of the graphω4g,4h+3is then discussed and the graceful labeling is presented in this paper. Italso proves thatsome special(r1,r2,...,r4g+4h+2) -corona of the graphω4g,4h+3are ofalternating graph.

cycle;corona;gracefulgraph;alternating graph

O157.5

A

2014-06-23

国家自然科学基金（11171273）

张政（1981—），男，讲师，研究方向为图论及其应用。

1005-0523（2014）05-0117-05