基于tikhonov正则化的图像恢复

张睿，靳彦培，裴巧

（河南师范学院数学与信息科学学院，河南信阳464000）

基于tikhonov正则化的图像恢复

张睿，靳彦培，裴巧

（河南师范学院数学与信息科学学院，河南信阳464000）

图像恢复问题一直伴随着数字图像技术的不断发展而发展.近年来图像复原的应用范围已经扩展到众多的科学和技术领域，如天文观测，物质研究，遥感图像，医学影像等.解反问题的正则化方法与最优化理论相结合可以在数字图像恢复中有很大的应用.本文首先介绍成像系统基本概念和理论，通过图像退化模型退化，然后采用基于tikhonov正则化方法，通过用CG最优化方法以及直接解正则方程组进行对图像进行恢复，最后通过数值试验进行图像恢复并简单比较两种方法图像处理的差异.

狄拉克δ；函数图像退化模型；BTTB矩阵构造；退化算子；tikhonov正则化；CG最优化方法

1 引言

数字图像恢复是图像处理的一个重要分支，它属于反问题的研究领域.其处理过程有许多方法，例如小波变换、傅里叶变换、Cosine变换等.而解反问题的正则化方法与最优化理论相结合可以在数字图像恢复中有很大的应用.本文采用基于tikhonov正则化方法，通过用CG最优化方法，以及直接解正则方程组进行对图像进行恢复，然后再进行比较，数值显示正则化方法是一种可靠有效的方法.

2 预备知识

2.0 成像系统

点源的概念：一幅图像可以看成由无穷多个极小的像素组成，每个像素可以看作为一个电源成像，因此，一幅图像也可以看成由无穷多点源形成的，在数学上，点源可以用狄拉克δ函数表示.二维δ函数可定义为

且满足

它的一个重要特性为采样特性即：

另一个特性为位移性：

2.1 图像退化模型

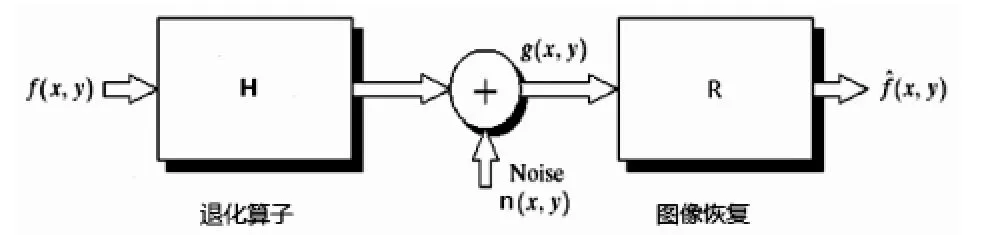
假定成像系统H是线性位移不变系统，则f(x,y)表示理想的、没有退化的图像，获取的图像g(x,y)表示为退化的图像.则有以下关系：

若受加性噪声n(x,y)的干扰，则退化图像可以表示为这就是线性位移不变系统的退化模型（如图1所示）.

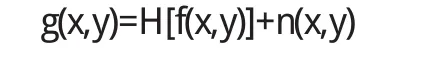
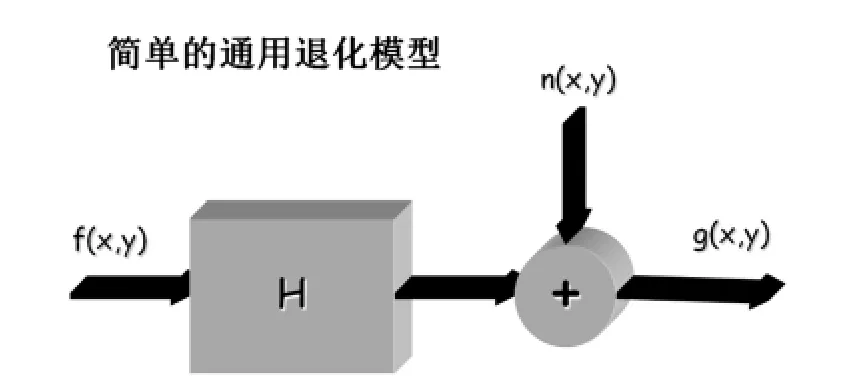
图1

2.2 连续图像退化的数学模型

在不考虑噪声情况下，连续图像经过退化系统H后输出：

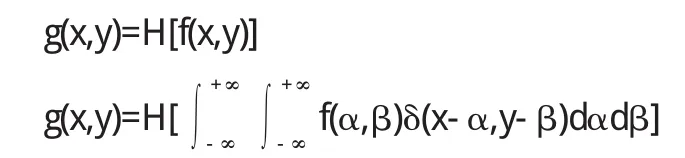
由于H为线性系统且为空间不变系统所以有：

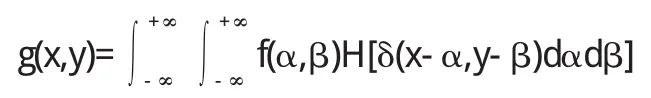
令

则

这里h(x-α,y-β)为退化系统的点扩散函数，或叫系统的冲击响应函数.只要知道退化系统的点扩散函数，就可以计算出降质的图像输出.

2.3 离散图像退化模型

为便于计算机实现，需将退化模型离散化.

2.3.1 先看一维卷积

对f(x)及h(x)均匀采样，样本M-1，即

f(x)x=0,1,...,M-1

其卷积为

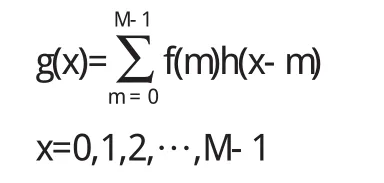
把f(x)、g(x)表示成向量形式：

卷积写成矩阵的形式：

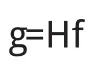
其中H是M*M的矩阵.

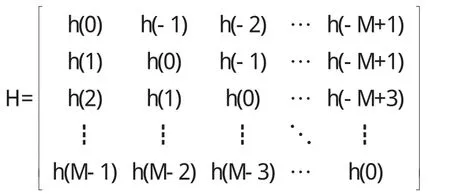
H为toeplitz矩阵.

2.3.2 推广到二维空间

设f(x,y)、h(x,y)均匀采样，样本数为M*N，M*N.

则循环卷积为

矩阵形式：g=Hf

f、g是MN维向量，H是MN×MN矩阵.

H是BTTB矩阵.

其中

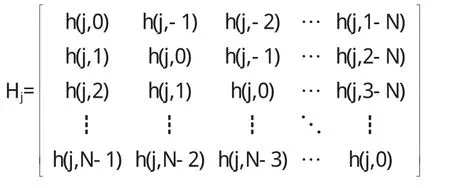
2.3.3 n是MN维噪声向量，则退化模型

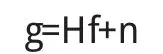
3 BTTB矩阵的构造

3.1 kronecker积的定义

显然，A⊗B是一个m12×n12的矩阵.

3.2 kronecker积的性质

若A、B分别为toeplitz矩阵则kronecker积为BTTB矩阵.

3.3 构造高斯退化算子

由于高斯分布函数为

且

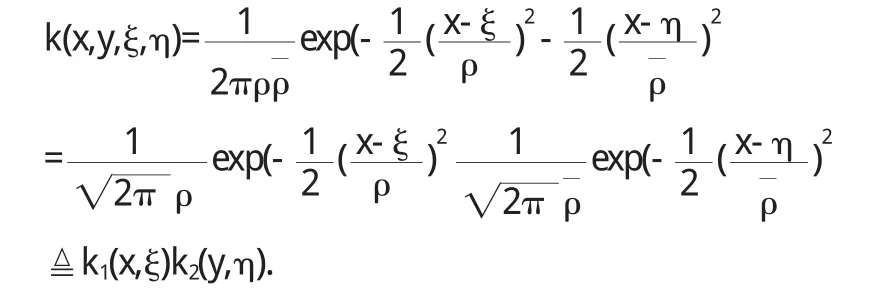
算子k的有限维近似可由对k1，k2的有限维近似并且作kronecker积得到.

4 正则化方法

4.1 目标

我们要做的事在知道退化算子H，知道图像g以及噪声类型的情况下，来反解出f，其近似解为.

其模型为：

4.2 用到的技术

4.2.1 tikhonov正则化

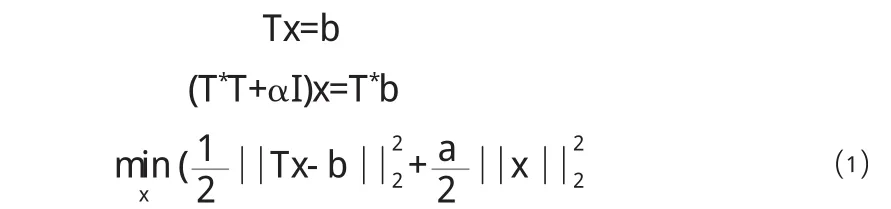
等价于

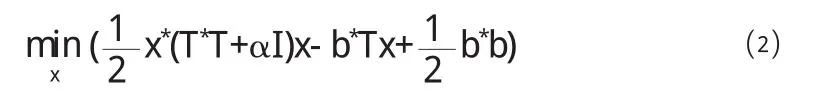
⑵转化为最优化问题.

4.2.2 共轭梯度求最小化

①给定初始点x0，计算p0=-▽f(x0)；置k=0；

②作直线搜索f(xk+tkpk)=minf(xk+tpk)；

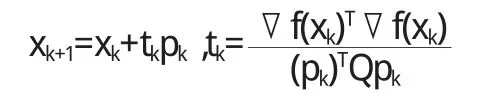
④计算

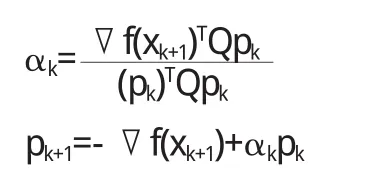
⑤置k=k+1；若k=n，停止，输出xk-1,否则转②

4.3数值实验

下面对一张像素分别为70*70，40*40,30*30（70*70为最大极限尺寸）的图片分别用两种方法做实验进行了比较，第一种方法用的是CG对（2）进行求极小值（每个共轭方向只搜索了一次结束），第二种是对正则化得方程（1）进行直接求解，并且分别对α取不同的值进行误差比较，及观察其误差趋势.如下图所示：

像素为70*70的结果

图像为40*40的结果

像素为30*30的结果

其中，图第一子图为原图片，第二子图为退化后的图像（这里我们取ρ==1.7），第三子图为用共轭梯度法求出的结果，第四子图为是对正则化得方程进行直接求解得到的图像.

5 恢复误差的评估

首先定义误差公式为：

其中f为真解，fˆ是求得的近似解.则有下表知

70*70图像40*40图像30*30图像cond值5.0545e+011 3.3254e+011 2.0448e+011 CG法误差值0.0710 0.1280 0.1494直接法误差值0.1162 0.1003 0.0940

有表格分析知，在问题不是很病态时直接法误差小些（α取最优值），当图像像素多、问题更病态时CG法好一些. 6参数选取与误差的关系

由下图分析可知，对于α的取值不同他们分别的误差也不同，CG方法做出来的基本上是随α值减小而减小，而直接解正则后的方程组（1）得到的误差是随着α值增加过程，误差先减小后增加，有一个最优解（70*70时间太长就不分析了）.

像素为40*40的图像

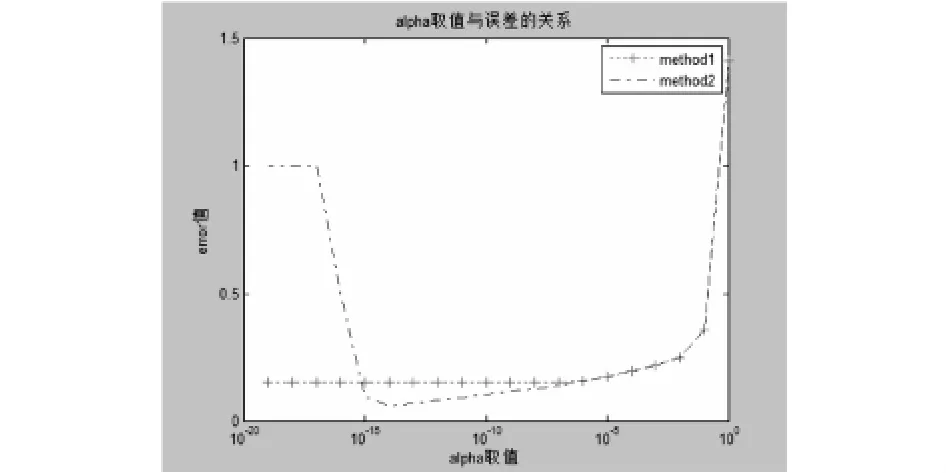
像素为30*30的结果

7 结论

对于tikhonov正则化方法，求解不适定问题比只要对α选取好参数，就可以反演出较好的解.

〔1〕姚敏，等.数字图像处理[M].机械工业出版社，2006.1.

〔2〕（美）Rafael C.Gonzalez,Richard E.W oods.数字图像处理（第二版）[M].北京：电子工业出版社，2005.

〔3〕肖庭延，于慎根，王彦飞.反问题的数值解法（计算方向丛书）[M].北京：科学出版社，2003.

〔4〕张平文，李铁军.数值分析[M].北京大学出版社，2007.

〔5〕曹静杰.反问题的最优化方法研究及其在图像恢复中的应用[D].北京交通大学，2008.

TP391

A

1673-260X（2014）05-0013-03