等价无穷小在求极限运算中的应用

孙卫卫，杜美华，孙建英

（青岛理工大学琴岛学院，山东青岛266106）

等价无穷小在求极限运算中的应用

孙卫卫，杜美华，孙建英

（青岛理工大学琴岛学院，山东青岛266106）

本文主要是讨论等价无穷小在极限运算中的应用.通过应用极限的四则运算法则证明,得到这样的结论：在求极限中的乘除运算与幂指函数的求极限当中，等价无穷小可以做到无条件的替换，而在加减运算中可以做到有条件的替[1]换.这样使得等价替换在型未定式的计算中可以有效的减少计算量，在一定程度上比洛必达法则求解问题更加的简捷.

极限；等价无穷小；等价替换；洛必达法则；未定式

在高等数学中，我们都了解等价无穷小在求极限的乘除运算中是可以替换的.

1 定理1

在自变量的同一变化过程中，若α1(x)～α2(x)，β1(x)～β2(x)，则有以下结论：

例1（1）

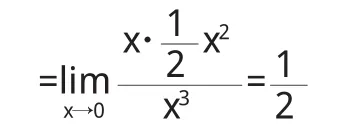
（2）

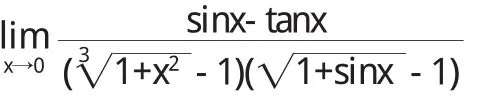
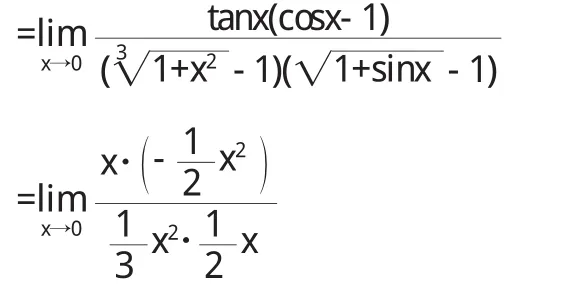
（3）

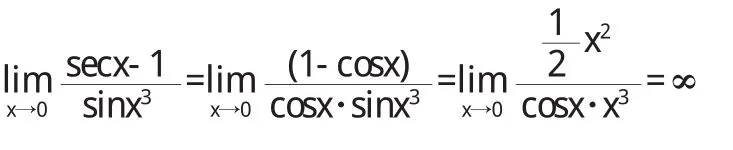
（4）

例2

如果在本题的分子中直接采用等价无穷小替换，也会得到同样的结果，即

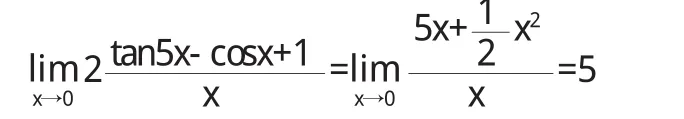
我们似乎感觉等价无穷小在加减运算中也是可以替换的，但是在例1中的（1）、（2）中若用等价替换：

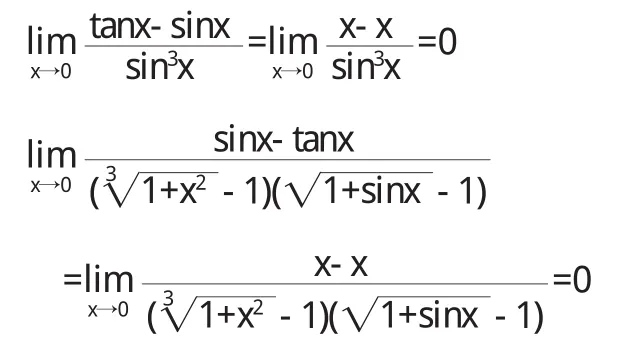
这样又会得到错误的结果.

2 定理2

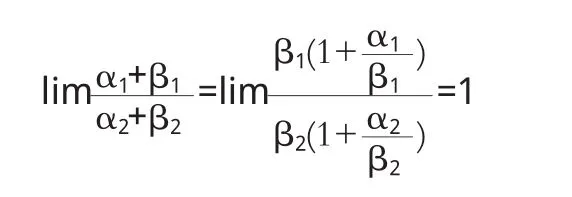
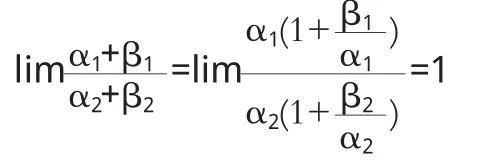
证毕.

证明

证毕.

例3（1）

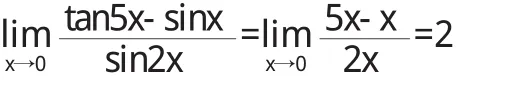
（2）

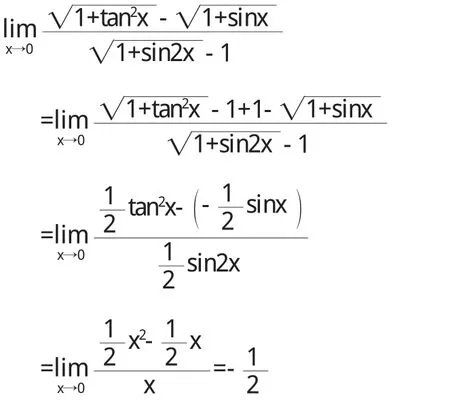
（3）

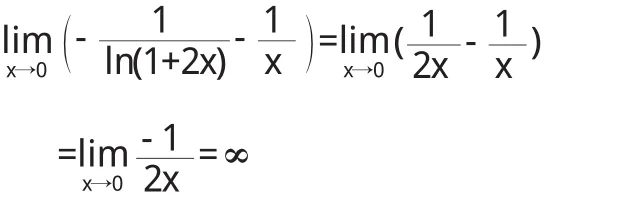
3 引理

证明

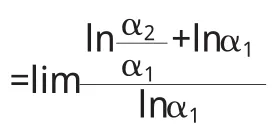
证毕.

证明

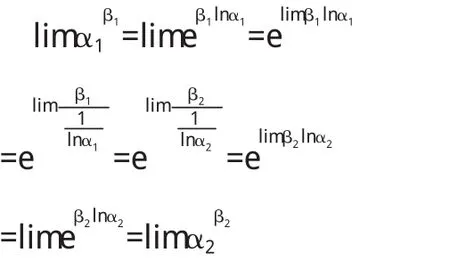
证明例4

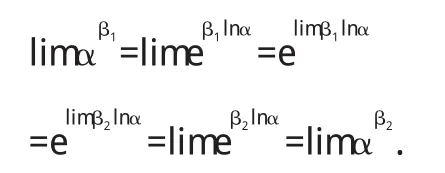
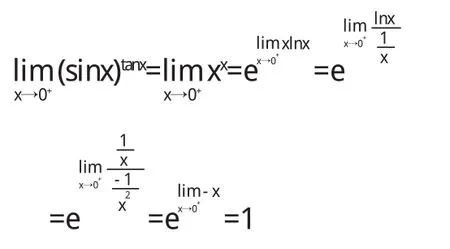
例5

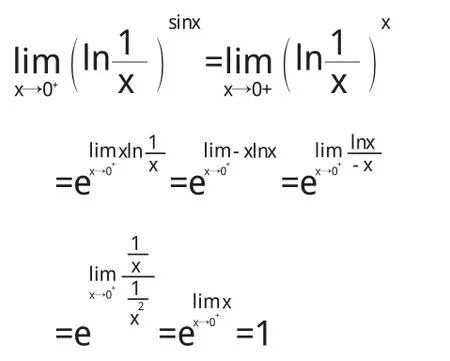
从本文中的例题中可以看出掌握等价替换的条件对我们求函数，数列的极限会有很大帮助，在某种程度上可以大大减少计算量.

〔1〕同济大学数学系.高等数学（上册）第六版[M].北京：高等教育出版社，2007.

O13

A

1673-260X（2014）05-0003-02