亚正定矩阵的充要条件

黄 毅

（1.成都大学 信息科学与技术学院，四川 成都 610106；2.模式识别与智能信息处理四川省高校重点实验室，四川 成都 610106）

0 引 言

对于矩阵正定性的研究，过去一直局限于实对称矩阵 和Hermite矩 阵.例 如，1970年，Johnson［1］引入了不再局限于实对称矩阵和Hermite矩阵的实正定矩阵的概念；1985年，Horn等［2］给出了实正定矩阵的定义，而李炯生［3］对广义正定矩阵的性质和特征做了较深入的研究；其后，屠伯埙提出了亚正定矩阵的概念，并对其做了较系统的论证与研究，认为实正定矩阵实际上就是亚正定矩阵，这2个概念是等价的，它们都是把实对称矩阵的限制去掉了［4－5］.本研究使用亚正定矩阵的概念，建立了亚正定矩阵的一些充分和必要条件.

1 定 义

先说明一些本研究使用符号：R 表示实数集；C表示复数集；Mn（P）表示数域P上n阶方阵的集合；Rn×1表示全体n维实列向量集合；Cn×1表示全体n维复列向量集合；AT表示矩阵A 的转置；¯A 表示矩阵A 的复共轭；A＊表示矩阵A 的共轭转置，即A＊＝¯AT.

定义1（实对称矩阵，实反对称矩阵，Hermite矩阵和反Hermite矩阵） 如果A ＝AT，矩阵A ∈Mn（R）称为实对称矩阵；如果A ＝－AT，矩阵A ∈Mn（R）称为实反对称矩阵；如果A ＝A＊，矩阵A ∈Mn（C）称为Hermite矩阵；如果A ＝－A＊，矩阵A∈Mn（C），称为反Hermite矩阵.

定义2（实对称正定矩阵） n 阶实对称矩阵A称为实对称正定矩阵，如果对于任一非零实向量，X∈Rn×1，都有XTAX ＞0.

定义3（实方阵的对称分支和反对称分支） 事实上，实方阵可唯一地表示成，

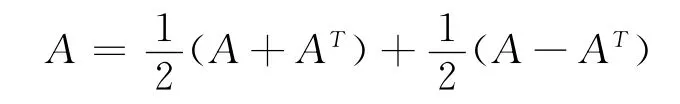
的分解形式.令，

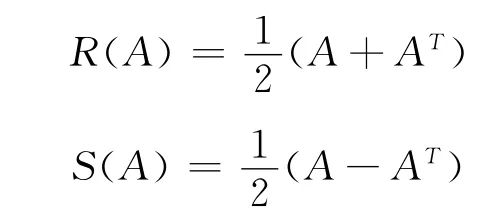
则，

A ＝R（A）＋S（A）.

其中，R（A）是实对称矩阵，称为实方阵A 的对称分支；S（A）是实反对称矩阵，称为实方阵A 的反对称分支.以下的分解式，A ＝R（A）＋S（A），均指这种意义的分解.

定义4（实正定矩阵） 设A ∈Mn（R），如果对于任一非零实向量，X ∈Rn×1，都有，XTAX ＞0，则称A 为实正定矩阵［1－3］.

定义5（亚正定矩阵） 如果实方阵A的对称分支R（A）是实对称正定矩阵，则称A 为亚正定矩阵［4］.

实正定矩阵和亚正定矩阵这2 个概念是等价的［4］，本研究使用亚正定矩阵的概念.“亚”字在汉语里有“次一等”的意思.顾名思义，亚正定矩阵就是满足的条件少于普通的实对称正定矩阵的正定矩阵.

定义6（主子阵和顺序主子序） 一个方阵中相同的行标和列标的行和列的交叉元素所形成的矩阵称为这个方阵的主子阵.一个方阵A 的k阶主子阵，

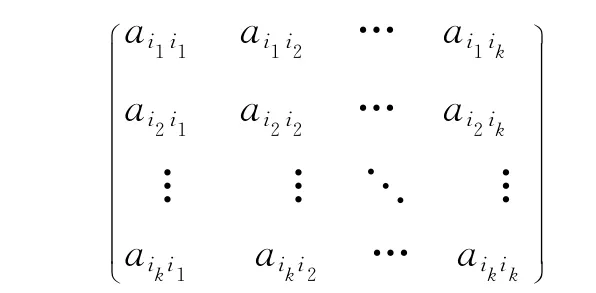
其中，1 ≤i1＜i2＜… ＜ik≤n，可用符号来表示.特别地，主子阵称为A 的k 阶顺序主子阵.

2 亚正定矩阵的充要条件

定理1 设A ∈Mn（R），则A 是亚正定矩阵的充分必要条件是，存在P ∈Mn（C）非奇异，使得，

证明

1）必要性.A 是亚正定矩阵⇔R（A）实对称正定⇔存在Q ∈Mn（R）非奇异，使得，

其中，In为n 阶单位矩阵.

因为，QTS（A）Q ∈Mn（R），所以，

故，QTS（A）Q 是反Hermite矩阵.由于实矩阵QTS（A）Q 的虚特征值共轭成对出现，且反Hermite矩阵的特征值为零或纯虚数，故QTS（A）Q 的特征值可以表示为，ib1，－ib1，…，ibs，－ibs，0，…，0，其中，bm＞0，m ＝1，2，…，s.

又，反Hermite矩阵QTS（A）Q 是正规矩阵⇔存在酉矩阵U 使得，

令，QU ＝P ∈Mn（C），则P 是非奇异矩阵，有，

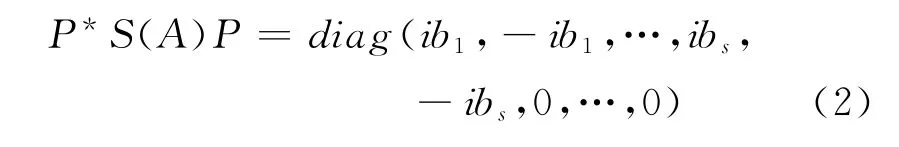
式（1）两端各自左乘U＊右乘U 得，

其中，In是n 阶单位矩阵.

式（2）＋式（3）得，

因为P＊和P 皆非奇异，一个矩阵乘上非奇异阵不改变秩，所以由式（2）得，

即，

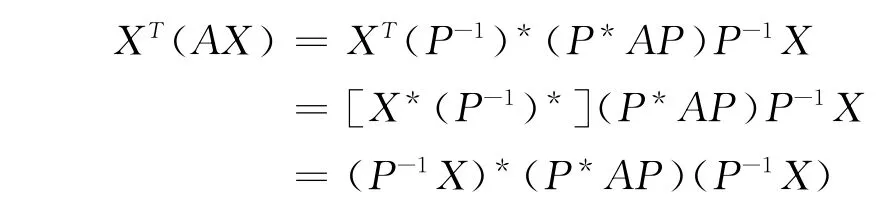
令，P－1X ＝Y ≠0，有，

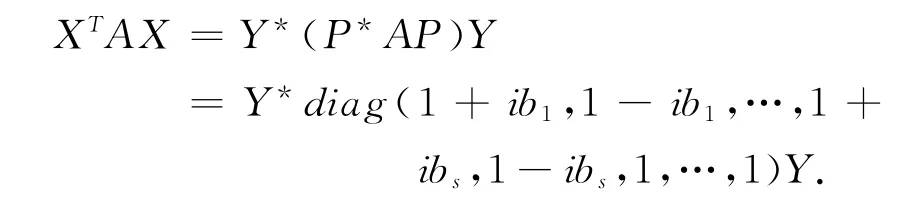
再令，Y ＝（y1，y2，…，yn）T，其中，yi∈C，且yi不全为零，i＝1，2，…，n，则，

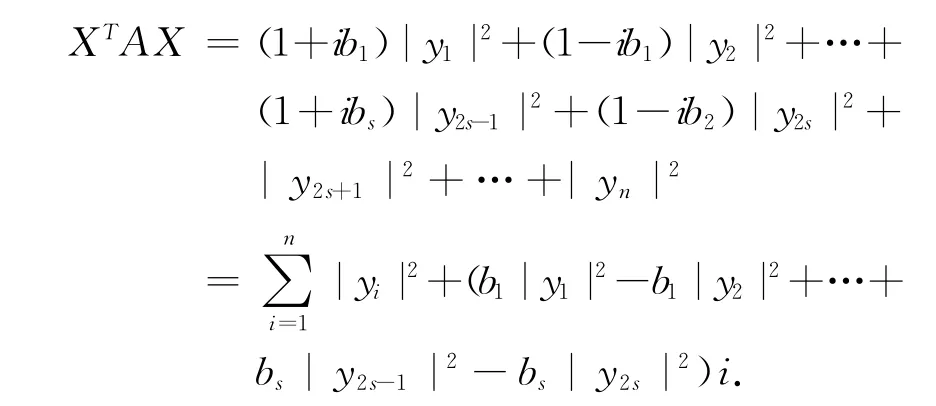
因，XTAX ∈R，由上式两端比较可得出，

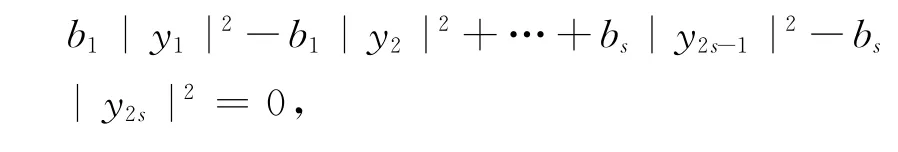
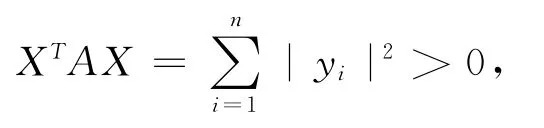
因此，A 是亚正定矩阵，

定理2 设A ∈Mn（R），则A 是亚正定矩阵的充分必要条件是，存在P ∈Mn（C）非奇异，使得，

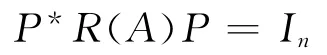
其中，In是n 阶单位矩阵.

证明

1）必要性.由定理1必要性的证明过程知式（3）成立.

令，P－1X ＝Y ≠0，有，

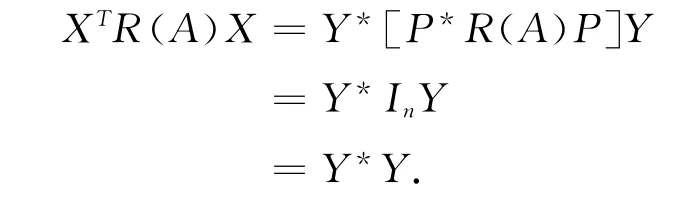
再令，Y ＝（y1，y2，…，yn）T，其中，yi∈C，且yi不全为零，i＝1，2，…，n，则，

所以，A 是亚正定矩阵.

定理3 设A ∈Mn（R），则A 是亚正定矩阵的充分必要条件是，存在P ∈Mn（C）非奇异，使得，

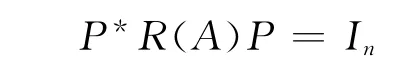
其中，In是n 阶单位矩阵，

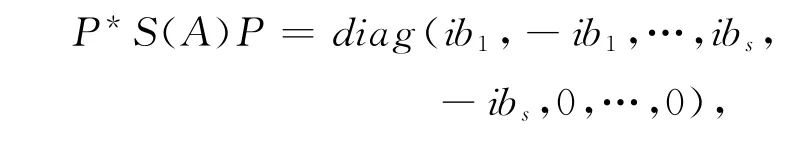
证明

1）必要性.由定理1 必要性的证明过程知式（2）、（3）成立.

2）充分性.由定理2知成立.

定理4 设A ∈Mn（R），则A 是亚正定矩阵的充分必要条件是，对任意实数t∈［0，1］，tA ＋（1－t）B 是亚正定矩阵，其中，B ∈Mn（R）是亚正定矩阵.

证明

故，tA ＋（1－t）B 是亚正定矩阵.

这一结论说明，n阶亚正定矩阵集合为一凸集.

2）充分性.令t＝1即得.

需说明的是，如果定理4中的条件t∈［0，1］改为t∈（0，1），就不能推出A 是亚正定矩阵.例如，设B 是亚正定矩阵，A ＝0，则t∈（0，1），有tA ＋（1－t）B＝（1－t）B是亚正定矩阵，但A ＝0不是亚正定矩阵.

当ann≠0时，

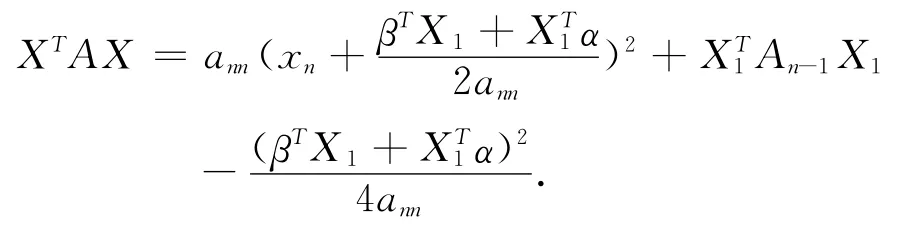
因 为，βTX1和XT1α都是数，所以βTX1＝，故，

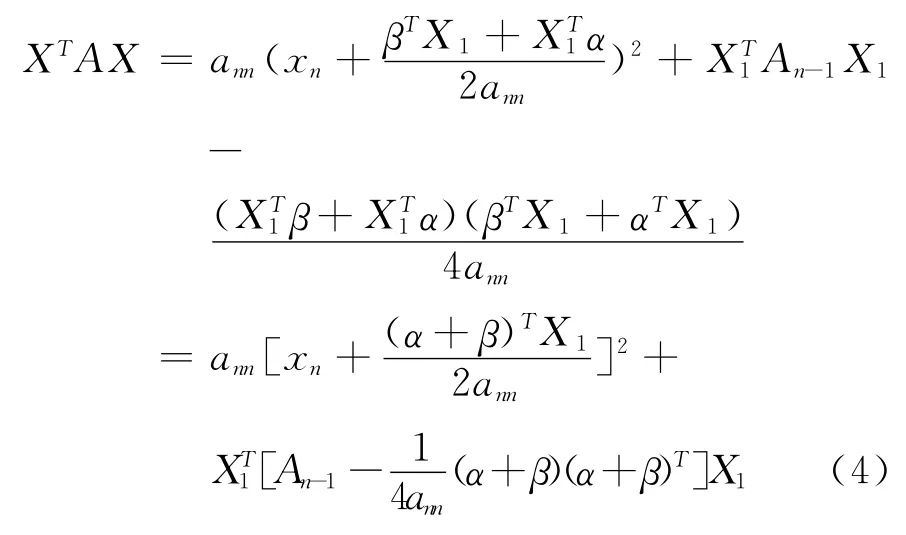
1）充分性.因ann＞0，且β）T是亚正定矩阵，故，当X1≠0时，由式（4）得，XTAX ＞0.当X1＝0时，必有xn≠0，由式（4）亦得XTAX ＞0.故A 是亚正定矩阵.

2）必要性.因为A 是亚正定矩阵，其主对角元素全 为 正 实 数［6］，故ann＞0，X1≠0，X1∈

R（n－1）×1，取，

由式（4）有，

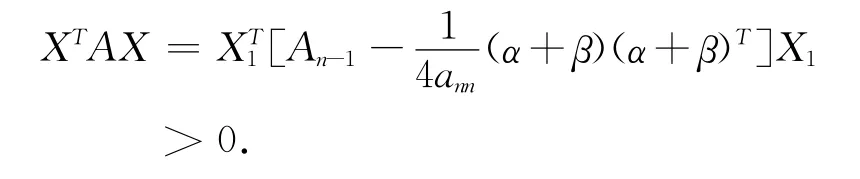
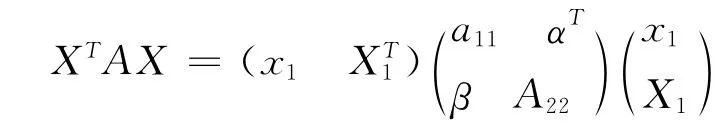
当a11≠0时，

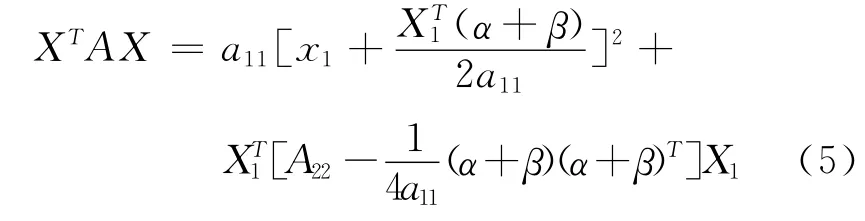
1）充分性.因a11＞0，且β）T是亚正定矩阵，故，当X1≠0时，由式（5）得，XTAX ＞0.当X1＝0时，必有x1≠0，由式（5）亦得XTAX ＞0.故A 是亚正定矩阵.

2）必要性.因为A 是亚正定矩阵，故a11＞0，X1≠0，X1∈R（n－1）×1，取，

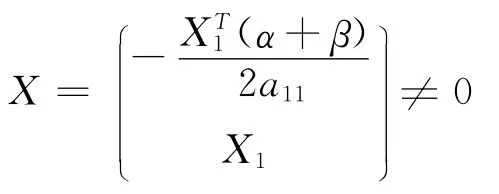
由式（5）有，

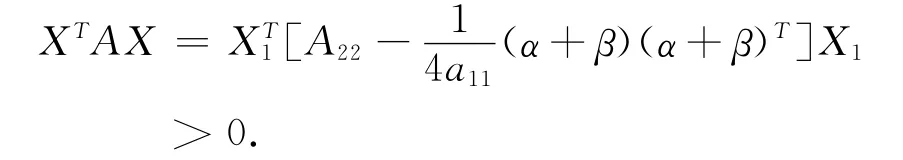
注意，定理5和定理6的2个充要条件给出了亚正定矩阵的2个降阶判别法.

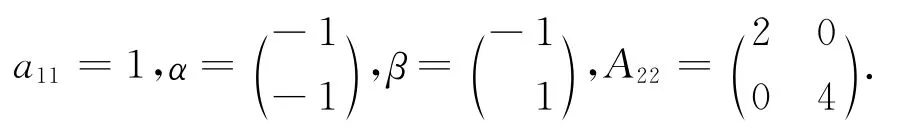
因为，a11＞0，

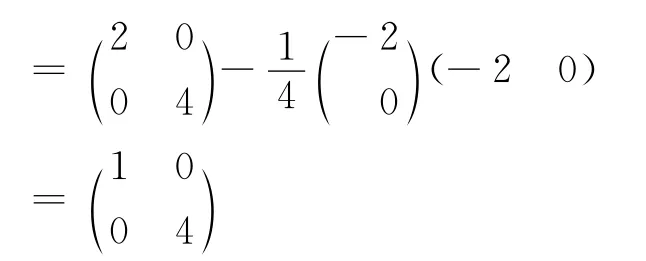
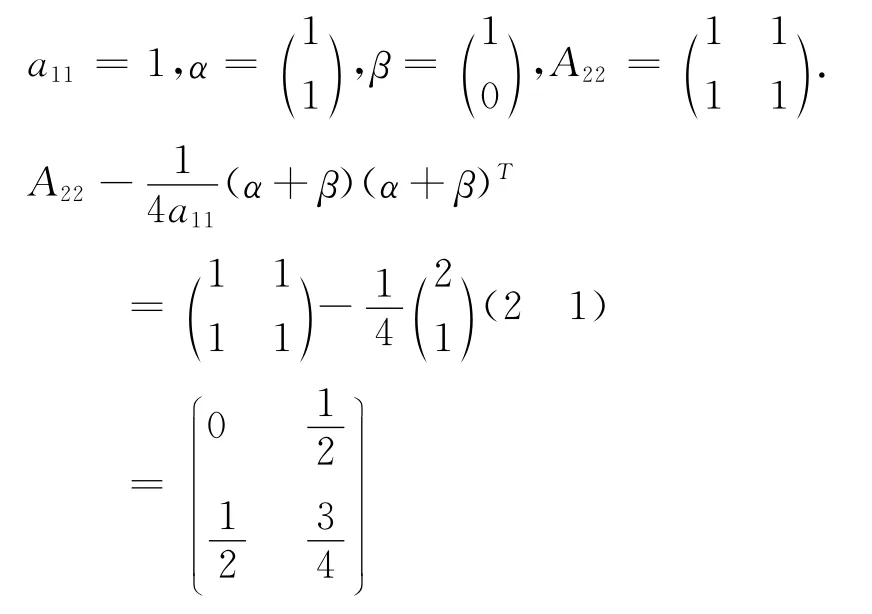
［1］Johnson C R.Positive definite matrices［J］.The American Mathematical Monthly，1970，77（3）：259－264.

［2］Horn R A，Johnson C R.Matrix analysis［M］.Cambridge：Cambridge University Press，1985.

［3］李炯生.实方阵的正定性［J］.数学的实践与认识，1985，15（3）：67－73.

［4］屠伯埙.亚正定阵理论（I）［J］.数学学报，1990，33（4）：462－471.

［5］屠伯埙.亚正定阵理论（II）［J］.数学学报，1991，34（1）：91－94.

［6］黄毅，欧鹏.亚正定矩阵的基本性质［J］.成都大学学报（自然科学版），2014，33（1）：20－22.