秩亏自由网平差在近景影像色彩均衡处理中的运用

詹总谦，饶友琢

(武汉大学测绘学院，武汉 430079)

1 引 言

色彩均衡处理是遥感影像预处理的重要环节之一。对于多张像片的色彩均衡处理，目前比较成熟、运用较为广泛的算法有基于Wallis滤波器的色彩均衡算法[1-2]和基于直方图匹配的色彩均衡算法[3-4]。Wallis 滤波器实际上是一种局部影像变换，它使得影像不同位置的灰度方差和灰度均值具有相近的数值，其处理效果和真实场景中的地物信息有关，如果不同影像范围内的地物整体信息变化不大，就能起到很好的效果[1-2，5-7]。直方图匹配方法可以用一幅影像对另一幅影像进行色彩重建[3]，但是它有可能会出现比较多的灰度级合并，使原影像中某些细小的反差消失；它也可能增大原有灰度级之间的相对距离，使某些反差增大。

潘俊[8]利用线性模型对航空影像色彩进行整体处理，再对重叠区域进行聚类分析，用不同类别的不同线性关系共同构成对影像间非线性关系的逼近，以此来进行重叠区域的局部优化，取得了较好的效果。孙明伟[9]通过假定区域内影像间重叠区域的灰度均值和方差具有特定的线性关系，并通过最小二乘解算出所有线性系数，最后通过Wallis变换对所有的影像色彩进行修正，也达到了正射影像的色彩一致性。Xiong等[10]在智能手机全景影像拼接方面，对影像的色彩和亮度校正做了一系列富有成效的工作。他们利用Gamma 校正来对序列影像的亮度进行校正以防止像素饱和，用线性系数来对影像色度进行校正，从而使得所有影像的亮度和色彩具有良好的过渡。该方法简单有效，使拼接的影像具有良好过渡并尽可能达到颜色保真。

相对于卫星和航空影像，近景影像受到拍照角度、光照入射角以及白平衡调整等众多因素的影响更为严重，从而导致序列影像的亮度和色调严重不同，最终影响影像的拼接融合、三维模型的可视化等。本文将秩亏自由网平差应用于近景影像的色彩均衡处理，实现对区域内影像的整体色彩修正，使拼接影像及三维模型的整体色调一致。

2 基于秩亏自由网平差的影像色彩均衡原理

2.1 基本思想

如果单幅影像内部已经消除了光照不均匀性，则影像之间的色彩差异主要表现为不同通道之间的整体亮度差异及色彩偏差。由于影像灰度均值反映了其色调与亮度[1]，则可以假设影像重叠区域灰度均值之间存在着如下线性关系：

ki·Xij+bi+ni(X)=kj·Xji+bj+nj(X)

(1)

其中，ki、bi表示第i幅影像灰度均值的乘性系数和加性系数(称为修正参数)，Xij表示第i幅影像与第j幅影像重叠部分的灰度均值，ni(X)表示随机噪声；kj、bj、Xji、nj(X)与前述各参数意义对应。

对测区内所有存在重叠关系的影像都可以列出如式(1)的方程，进而利用最小二乘原理解算出修正参数的最优解，即满足：

(2)

ΔXi,j=(ki·Xij+bi)-(kj·Xji+bj)

(3)

2.2 秩亏自由网平差模型

根据测量平差原理可知，由式(1)所得的误差方程解算缺乏必要起算数据，对应系数阵非列满秩，因此方程解算属于秩亏自由网平差问题。

根据秩亏自由网平差原理，为了保证方程具有唯一解，需要引入基准条件，而基准条件数等于必要起算数据个数。这里取待处理影像中某幅色彩较好的影像为基准影像，即其对应的乘性系数k取值为1，加性系数b取值为0。实验发现，k和b实际是一组线性相关值，在平差处理时容易造成b对k的吸收，孙明伟在求解方程组时对k和b分开求解。实际上加性系数数值极小，因而式(1)可以只保留乘性系数k，从而保证线性方程的严密数学关系，则式(1)表达为：

ki·Xij-kj·Xji=0

(4)

另外，为了使得处理后的影像在亮度上也达到均衡，可以引入约束条件：

KIi·Ii=Ir

(5)

其中，Ii表示第i幅影像的亮度均值，KIi为对应的修正系数，Ir表示参考影像的亮度均值。

对区域内所有影像的所有通道按式(4)和式(5)列出方程组，并通过最小二乘求解，就能对所有影像色彩进行校正处理。

2.3 重叠区域有效像素的选取

影像重叠区域的灰度均值取决于重叠区域内有效像素的选取，它对色彩均衡的效果产生重大影响。为了减少配准误差对重叠区域选取的影响，同时避免因摄影角度造成近景影像内地物内容变化的影响，可以利用相关系数对重叠区域内的像素进行筛选。如图1所示，通过相关系数筛选出来的有效像素几乎全部是重叠影像间的相同地物部分。

图1 利用相关系数对近景影像重叠区域进行有效像素筛选的效果(黄色部分)

2.4 色彩均衡处理的效率改善

近景影像一般重叠较大，测区内影像间的重叠关系也较多，因而重叠区域均值计算量较大。实际处理中，可以采用金字塔技术和多核并行处理技术提高运算效率。

2.4.1 利用金字塔技术提高重叠区域灰度均值计算效率

通过对影像重叠区域进行金字塔处理，并在金字塔影像中进行像素筛选和灰度均值计算可以有效提高效率。

金字塔技术可能会降低图像处理的精度。图2是利用金字塔和没有利用金字塔计算的图像灰度均值的对比图，图2中R表示原始图像R通道的灰度均值，R′对应利用金字塔技术得到的灰度均值。从图中可以看出两者差别极小。同理，绿通道和蓝通道也可证明相同的结论。

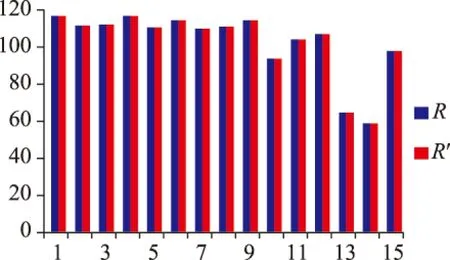
图2 金字塔处理前后的图像灰度均值对比(R通道)

2.4.2 利用并行计算提高灰度均值计算和图像保存的效率

对于图像重叠区域灰度均值计算、图像色彩校正以及保存等操作，可以利用并行处理技术提高处理的效率。针对一般的共享存储体系计算机，可以利用openMP技术实现并行化处理。表1和表2分别是加入openMP并行处理后的操作时间对比(Intel i7 4核处理器)。

表1 openMP并行处理前后的图像灰度均值计算时间对比

表2 openMP并行处理前后的图像色彩校正及保存的时间对比

2.5 精度评价指标

根据秩亏自由网平差色彩均衡原理，这里可以采用重叠区域之间灰度均值差值的中误差进行精度评定，具体表达成下式：

(6)

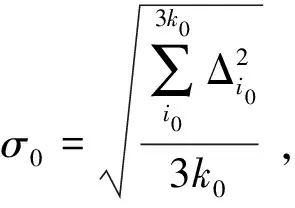
3 实验分析

图3(a)和图3(b)是两组近景影像色彩均衡处理前后拼接结果的对比图。在运用本文算法之前，如果单幅影像内部存在色彩不均匀，则需要进行单幅影像的匀光处理，本文采用经典的MASK匀光法[11]进行单幅影像的匀光处理。从图中可以看出，没有经过色彩均衡处理而直接拼接成的影像的色彩和亮度无法达到一致性(图3(a)与图3(b)的上图)；而经过本算法处理后拼接而成的影像色彩非常均衡。

图3(a)由6幅影像拼接而成，色彩均衡前后的指标值分别为：σ0=25.54和σ1=1.25；图3(b)由12幅影像拼接而成，色彩均衡前后的指标值分别为：σ0=25.09和σ1=1.53。结果表明，处理后的影像色彩均衡效果非常明显。

图4是色彩均衡处理前后的三维模型对比图。对比验证，经过本文色彩均衡方法处理后的模型纹理色调趋于一致。

图3 近景影像色彩均衡处理前后对比

图4 色彩均衡处理前后的三维模型对比

4 结束语

近景影像成像影响因素多，色调和亮度变化大，具有一定的特殊性。本文将秩亏自由网平差用于近景影像的色彩均衡处理，取得了良好的效果，对于近景影像的拼接和三维模型的纹理映射具有非常重要的作用。

参考文献：

[1] 李德仁，王密，潘俊.光学遥感影像的自动匀光处理及应用[J].武汉大学学报，信息科学版，2006，31(9)：753-756.

[2] SUN M W，ZHANG J Q.Dodging research for digital aerial images[J].The International Archives of the Photogrammetry，Remote Sensing and Spatial Information Sciences，2008，37：349-353.

[3] 王邦松，艾海滨，安宏，等.航空影像色彩一致性处理算法研究[J].遥感信息，2011，(1)：45-49.

[4] 常志华，王子立.一种基于直方图匹配的颜色校正方法[J].科技资讯，2007，(13)：206-207.

[5] 王智均，李德仁，李清泉.Wallis变换在小波影像融合中的应用[J].武汉测绘科技大学学报，2000，25(4)：338-342.

[6] 张力，张祖勋，张剑清.Wallis滤波在影像匹配中的应用[J].武汉测绘科技大学学报，1999，24(1)：24-27.

[7] 林景亮，陈岳林.多摄像机图像拼接自动色彩均衡算法[J].计算机应用，2010，30(12)：3236-3237.

[8] 潘俊.自动化的航空影像色彩一致性处理及接缝线网络生成方法研究[D].武汉：武汉大学，2008.

[9] 孙明伟.正射影像全自动快速制作关键技术研究[D].武汉：武汉大学，2009.

[10] XIONG Y，PULLI K.Color and luminance compensation for mobile panorama construction[A].International Conference on ACM Multimedia 2010，Firenze，Italy，1547-1550.

[11] 王密，潘俊.一种数字航空影像的匀光方法[J].中国图象图形学报，2004，9(6)：744-748.