以DEM为高程辅助的弱交会卫星影像的区域网平差
曹宁,张力,杜全叶
(1.兰州交通大学,兰州 730070;2.中国测绘科学研究院,北京 100830)
1 引 言
卫星遥感数据是国内外地图测制与更新的重要地理空间信息源。随着对地观测技术的重大进步和一些庞大计划的实施,资源遥感已进入新的发展时期,卫星测绘制图技术取得了重大进展。卫星测绘作为地理国情监测的重要技术手段,对国家基础地理信息的获取以及更新有着不可替代的作用。
与航空影像不同,高分辨率遥感卫星大多采用CCD线阵推扫成像模型,每一行影像都有一组外方位元素。基于此特征,卫星影像的成像模型多采用有理函数模型(Rational Function Model,RFM)描述物方到像方的映射关系。目前多数卫星影像供应商将有理函数模型的系数(RPC)作为影像元数据的一部分供应给用户。区域网平差也多采用有理函数模型组合仿射变换定向参数进行区域网平差。在实际数据生产中存在大量直下视影像,即影像中心投影射线近似垂直于地面;此外,卫星在太空中航行,其探测器的视场角(Field Of View,FOV)很小,由此导致重叠影像的基线航高比很小。近似垂直于地面的投影方式加之重叠影像很小的基线航高比导致同名点交会角普遍较小。例如,ZY-3相邻轨道直下视影像的交会角一般小于5°。该类影像(弱交会影像)若仍采用传统的模型进行平差将会造成连接点高程误差放大进而导致区域网平差无法收敛。陈良建等[1]研究了严密模型下用DEM辅助平差的理论。Teo T A[2]等比较了DEM辅助下不同平差模型对结果精度的影响。目前,我国大部分地区的基础测绘产品已经完成,针对已有地理信息进行测绘产品的生产具有快速、节约成本等众多优点。弱交会卫星影像的区域网平差理论正是从此角度出发。该理论对快速更新基础地理信息有重要意义。
2 以DEM为高程辅助的弱交会卫星影像的区域网平差
2.1 RFM及区域网平差模型
RFM是多种传感器模型的一种更通用的表达方式,适用于各类传感器包括最新的航空和航天传感器,可以理解为一种广义、通用的传感器模型。RFM从数学角度利用有理多项式建立物方(地面三维坐标)到像方(影像像素坐标)的映射关系。如式(1)[3]所示。
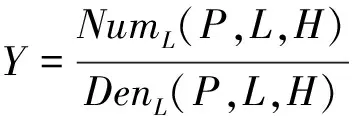
(1)
其中,(X,Y)为归一化像点坐标,(P,L,H)为归一化物方点坐标,NumL,DenL,NumS,DenS为一般多项式,多项式中每一项中各坐标分量的幂不超过3,并且各坐标分量之幂的总和也不超过3,共有20种组合。多项式系数称为有理函数系数,多项式的一次项用于描述由光学投影引起的变形,二次项用于描述由地球曲率、大气折射及镜头畸变引起的变形,三次项用于描述传感器振动以及其他未知因素所造成的变形。
目前,线阵影像多采用RFM组合仿射变换定向参数进行区域网平差,且平差在像空间进行,即将像方仿射变换加在RFM上组成区域网平差模型,数学模型如下:
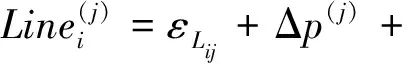
(2)

p(j)(Latitudei,Longitudei,Heighti)=Y·LINE_SCALE+LINE_OFF
r(j)(Latitudei,Longitudei,Heighti)=
X·SAMPLE_SCALE+SAMPLE_OFF
Δp,Δr即为仿射变换方程,数学模型如下:
Δp=a0+aS·Sample+aL·Line
Δr=b0+bS·Sample+bL·Line
(3)
式(3)中,a0、b0,aS、aL、bS及bL为仿射变换系数。其中,a0、aS及aL用于改正传感器在扫描方向上和姿态误差所引起的影像列方向上的误差,b0、bS及bL改正传感器在飞行方向上和姿态误差所引起的影像飞行方向的误差[4]。这6个参数和RFM模型系数共同构成严格成像几何模型参数。
对于区域网平差中的控制点或者连接点,都可以列出如式(4)的两个方程。对每一个点列出方程,组成误差方程组,按照最小二乘原理对仿射变换参数以及连接点物方坐标进行解算[5]。对于本文中涉及的弱交会连接点,其误差方程中不需要对该点高程值进行改正,区域网平差中每种类型点的误差方程的列取方法在本文2.3部分进行说明。
V=AX1+BX2-l
(4)
其中,

2.2 影像预处理
在区域网平差中,若将同组影像的同名点视为一般连接点会导致平差法中方程不可逆。对于该类同名点需要根据已知的同组信息将其剔除,或者按照弱交会连接点来对待。对于同组影像的自动识别可根据影像元数据文件中记录的影像类型、开始扫描时间以及结束扫描时间来进行,例如对于资源三号影像可以由元数据文件中的SensorID、StartTime、EndTime字段来识别。
在大面积区域网平差中,连接点包括两种类型:一般连接点和弱交会连接点,在区域网平差之前需要识别出弱交会点。交会角是指同名点中各点与其对应的摄影中心连接所形成射线的夹角。若交会角较小,在区域网平差中便将其视为弱交会点。对于线阵影像,无法获取对应像方点的摄影中心,但根据RFM以及像点坐标可得到其投影光线的空间向量坐标。识别弱交会连接点的具体做法是:首先,给定任意高程值,根据RFM以及同名点各点坐标,反解出该高程对应的大地坐标。然后,给定与之前相异的高程值,按照同样的方法解算出其大地坐标。此时,获取了同名点各投影光线上的两个空间点三维坐标,计算各投影光线的空间单位向量,按照两向量夹角公式即可求出其交会角。
2.3 以DEM为高程辅助的弱交会卫星影像的区域网平差技术流程
针对存在弱交会连接点的区域,本文采用以DEM辅助的方法进行平差。技术流程如图1所示。
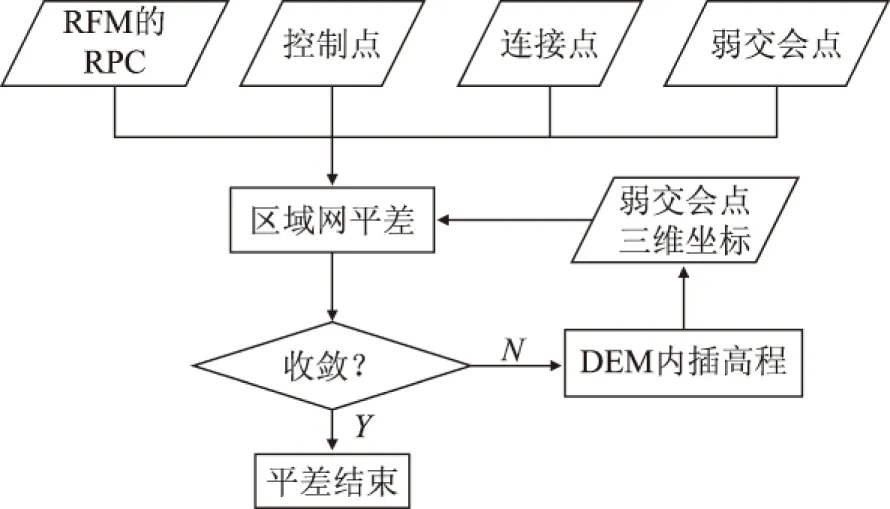
图1 DEM辅助高程区域网平差技术流程图
首先,根据弱交会连接点其中一点所在影像的RPC参数、该点的像方坐标以及DEM解算出该点的物方坐标,用同样的方法解算出同名点的物方坐标(图2),由同名点各影像坐标S1、S2,各片RPC参数以及DEM分别求出同名点各高程值Z1、Z2以及平面坐标,求出该点的中点坐标值作为弱交会点的平差初始值[6]。由影像的RPC参数、控制点、连接点以及弱交会连接点进行区域网平差,平差后对影像仿射变换参数、连接点物方坐标、弱交会连接点物方平面坐标进行改正,若平差结果收敛,平差结束。否则,根据弱交会连接点物方平面坐标内插出该点的新的高程作为该点新高程值,进行下一次平差,直到解算结果收敛,平差结束。该方法每次将弱交会连接点的高程值控制在DEM的合理范围内,因此能够有效减小弱交会连接点各点物方坐标的差值。

图2 弱交会连接点初始高程计算
在区域网平差迭代过程中,对于控制点以及连接点按照式(4)列误差方程,即每个点的误差方程中除包含仿射变换参数改正数以外还包含该点的物方三维坐标改正数。而对于弱交会连接点,其误差方程不需要对该点的高程进行改正,只包含仿射变换参数改正数以及物方平面坐标改正数。
3 区域网平差实验及精度评定
实验区域选取了8景资源三号直下视卫星影像(图3),左、右4景影像分别为同一条带(同组影像)。控制点数量8个,弱交会连接点数量为37个,弱交会点的交会角度最大不超过5°。使用DEM的格网间隔为30m。同条带影像连接点按弱交会连接点处理。影像分布及点分布如下图3所示,其中带圆圈的十字丝表示控制点,其他十字丝为弱交会连接点。
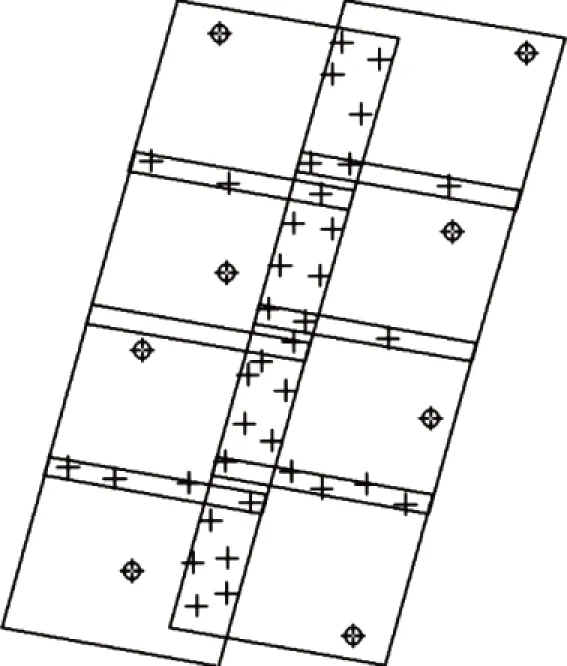
图3 影像分布及点分布图
实验按照本文2.3节的流程进行。精度评定方法采用在物方坐标系上进行,即利用平差后影像的RFM参数和仿射变换参数、点像方坐标、DEM求出的该点的物方坐标,将求出的物方坐标和平差所得该点的物方坐标进行比较。结果如表1所示,定向中误差为0.45像素。
4 结束语
区域网平差是生产正射影像环节中的重要步骤,对于弱交会卫星影像不能采用传统的平差方法进行作业。目前地理国情监测源数据中正存在着大量的弱交会卫星影像,例如:WorldView、QuickBird等,其相邻影像的交会角度多小于10°。利用本文提出的以DEM辅助弱交会卫星影像的区域网平差方法进行数据生产,其精度满足要求。可靠性也在各类弱交会影像的处理中得到了验证。
本文仅以DEM辅助弱交会卫星影像的理论做了详细的阐述,并证明了理论的可行性。下一步可在DEM精度、控制点数量对平差结果影响等方面进行深层次探讨。
参考文献:
[1] 陈良健,仝宜中.以DEM为高程控制之弱交会几何卫星影像区域平差[J].航测及遥感学刊,2007,12(1):17-35.
[2] TEO T A,CHEN L C,LIU C L.DEM-Aided block adjustment for satellite images with weak convergence geometry[J].Geoscience and Remote Sensing,2010,48(4):1907-1918.
[3] GENE D,GRODECKI J.Block adjustment with rational polynomial camera models[C].Proceedings of ASPRS 2002 Conference,Bethesda,Maryland,April 2002.
[4] 张力,张继贤,陈向阳,等.基于有理多项式模型RFM的稀少控制SPOT-5卫星影像区域网平差[J].测绘学报,2009,38(4):302-310.
[5] 隋立芬,宋力杰.误差理论与测量平差基础[M].北京:解放军出版社,2004.
[6] 吴颖丹,明洋.基于有理函数模型的多源SAR遥感影像区域网平差[J].测绘科学,2012,37(2):49-51.
[7] 王之卓.摄影测量原理[M].武汉:武汉大学出版社:2007.

