外载作用下悬跨管道纵向振动响应研究*

赵明明，熊 琎

(1. 辽河石油工程建设监理有限公司，辽宁 盘锦 124010； 2. 江汉石油钻头股份有限公司， 湖北 武汉 430233)

外载作用下悬跨管道纵向振动响应研究*

赵明明1，熊 琎2

(1. 辽河石油工程建设监理有限公司，辽宁 盘锦 124010； 2. 江汉石油钻头股份有限公司， 湖北 武汉 430233)

管道是油气资源运输的载体，其性能对作业安全影响巨大。在合理假设的基础上，通过建立悬跨管道的振动力学模型，建立并求解其运动微分方程，得到悬跨管道的纵向振动响应。管道在受冲击载荷作用时由于阻尼的存在其纵向振动响应幅值随时间逐渐减小；管道受一般外载作用下的响应可通过将外载视为作用时间段内冲击载荷的积分来处理；管道受简谐力作用时其振动幅度与阻尼比和频率比相关，当外激频率接近固有频率时振幅放大系数最大，当外激频率大于固有频率时，频率比越大管道的振幅放大系数越小。

外载；悬跨管道；纵向振动；阻尼；频率

1 引 言

石油天然气是保障国发经济发展和国家安全的重要能源，而管道又是石油天然气资源转移的主要运输载体。使用管道输送油气已在全球范围内普及，在我国仅由管道输送的原油便已占原油运输总量的90%[1-2]。管道输送能广泛应用的原因是：所需输送的介质量大，管道运输占地少且受地形限制较小，密闭安全可长期稳定运行，受天气影响较小，运输损耗小且成本低[3-5]。基于其具有的众多优势，国内外大量学者和技术人员对管道特别是管道建设进行研究。

在油气管道的铺设过程中，经常会遇到复杂的海底或陆地地质环境(例如山坡、洼地、江河等)，当管道裸露于不平坦的海床或地面时便形成悬跨管道[6]。悬跨管道两端承受支撑而中部悬空，由此造成管道的受力和运动复杂化。在悬空管道的服役过程中，管道内部流体的流动使管道产生涡激振动，这种振动容易引起管道的疲劳破坏[7]。与此同时，管道还可能承受外加载荷的作用，例如冲击载荷。

对管道的研究主要集中于管网设计方面，由于对管道的大量使用和研究，在其力学行为和运动特性方面也有不少研究[8-9]。根据悬跨管道的物理特性，可将其视为两端固支梁模型进行受力与运动分析[10]。目前国内外已有不少关于悬跨管道的受力特性的研究[11-13]，这些研究对管道的应用贡献巨大。对于悬跨管道运动方面，相关研究较少，而悬跨管道在特殊载荷作用下的振动研究也鲜见报道。笔者通过建立悬跨管道的力学模型，建立并求解其运动方程，得到悬跨管道在外载作用下的纵向振动响应。

2 振动模型

建立悬跨管道受外载时的单自由度纵向振动简化模型如图1所示。在分析其振动响应之前建立如下基本假设：①假设悬跨管道两端为固支边界；②将悬跨段管道质量集中于管道中间；③将管道中的流体视为附加于管道上的质量。

图1 振动简化模型

图1中，m为系统质量，c为系统纵向运动的阻尼，k为系统刚度，F为外载。将系统视为两端固定梁，其刚度为[14]：

(1)

式中：E为管道的弹性模量，l为管道悬跨长度，I为管道截面的主惯性矩，其计算公式为：

I=π(D4-d4)/64

(2)

式中：D为管道外径；d为管道内径。

3 模型求解

3.1 冲击载荷作用响应

假设悬跨管道系统初始时刻静止，系统在冲击作用下的响应可视为受到冲量时的响应，即假设系统在t=0时受到一个冲量I作用。实际中悬跨管道为一个有阻尼系统，其运动微分方程为[15]：

(3)

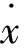
(4)

式中：ε为无限小量。

在分析冲击载荷的作用时，由于冲量在短时间内施加到系统，因此可认为该瞬时系统位移保持不变，而只是获得一个速度，冲击结束后，系统为自由振动。因此方程式(3)可等价为：

(5)

实际中的大多数系统阻尼比都小于0.2，故此处假设悬跨管道系统为欠阻尼系统，得到其纵向振动位移响应为：

x(t) =g(t)I

(6)

如图2所示为系统的纵向振动响应，由图可知，在承受冲击载荷后，由于阻尼的作用系统的振幅逐渐减小，通过调节系统固有特性如质量、刚度和阻尼等都可达到改变系统最大振幅的目的。

在谐波力作用下疲劳是破坏产生的主要因素，但冲击载荷作用下它不是最重要的。冲击使系统位移、速度和加速度都发生明显的增大，使得管道应力剧烈变化。在实际设计中应根据系统冲击响应确定冲击放大系数，得到作用于管道上的动载荷，由此确定管道的最大弯曲应力，确保冲击所造成的应力在许用范围之内。

图2 冲击载荷作用下系统响应

3.2 一般力作用响应

当系统受任意外力F(τ)作用时，这个力可看成由一系列大小变化的总量组成，如图3所示。假设在τ时刻外力F(τ)在Δτ内作用在系统上，则其冲量为F(τ)Δτ。对任意时刻t，冲量发生作用的时间为t-τ，那么该冲量在t时刻引起的系统响应为：

Δx(t)=ΔτF(τ)g(t-τ)

(7)

图3 任意力函数

系统在时刻t的总响应等于作用于所有τ时刻的微冲量引起的响应总和，即：

(8)

即悬跨管道任意激励F(t)下的响应为：

(9)

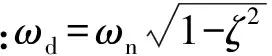
对一般外载的振动，振动响应由力函数的变化决定。对于振动响应的具体处理，当外载为任意波形的周期力时，可将外载用具有不同频率的简谐函数的叠加即傅立叶级数表示。如果外载为非周期的，在计算系统响应时，可通过傅立叶积分来代替激振力，也可用拉普拉斯变换或其他方法来处理。

3.3 简谐激励作用响应

假设激振力为F(t)=F0cosωt，则悬跨管道的运动微分方程为：

(10)

式中：F0表示外力的振幅，ω为外激频率。

方程式(10)为一个二阶非齐次线性微分方程，其解可转化为求通解和特解之和得到。求解后得到悬跨管道系统的响应为：

x(t)=X0e-ζωntcos (ωdt-φ0)+Xcos (ωt-φ)

(11)

其中：

(12)

(13)

(14)

(15)

静态力F0作用下的变形为：

δst=F0/k

(16)

定义振幅放大系数：

(17)

式中：r=ω/ωn为频率比。

图4为悬跨管道系统响应的振幅放大系数随频率比的变化曲线。由图可知，对于任意确定的频率比，阻尼越大，则M值越小；在发生共振或共振区附近，阻尼的存在将显著降低M值。

图4 振幅放大系数随频率比的变化

对于承受简谐载荷的悬跨管道系统，可根据载荷的频率特性，通过改变系统的设计参数如系统的固有振动属性、增大系统黏性阻尼系数的影响、增加减振器等来调整系统的振动响应，以达到管道的安全作业。由图4可知，在共振区的右侧，频率比越大，悬跨管道系统的振动幅值越小。

4 结 论

悬跨管道服役于恶劣环境下，承受各种载荷，不可避免地存在振动。该文从悬跨管道的纵向振动出发，通过建立悬跨管道的振动模型，建立系统运动微分方程，得到其在冲击载荷作用、一般载荷作用和简谐载荷作用下的振动响应。

系统在冲击载荷作用下的振动响应幅值由于阻尼的存在随着时间的推移逐渐减小；对于一般外力载荷，其可视为在力的作用时间段内冲击载荷所引起振动响应的叠加，具体的响应方程由作用力的函数确定；对于简谐振力作用下的管道振动响应，振幅放大系数与结构本身属性、阻尼比和频率比都有关系，系统的振动应尽量避免出现在共振区，同时通过改变系统的结构参数、黏性阻尼和增设减振装置等方法都可达到抑振或减振的目的。

[1] 张传平, 严大凡. 输气管道的输量、运距与管输费率关系研究[J]. 中国石油大学学报(社会科学版), 2006, 22(3): 17-19.

[2] 于树青, 刘春阳, 董 颖, 等. 管道建设项目后评价综合评价法与指标体系研究[J]. 石油工程建设, 2007, 33(3): 8-16.

[3] 王 晓, 郝芳华, 程红光, 等. 复杂地形高含硫输气管道环境风险事故模拟[J]. 中国环境科学, 2008, 28(1):78-82.

[4] 董绍华, 杨祖佩. 全球油气管道完整性技术与管理的最新进展——中国管道完整性管理的发展对策[J]. 油气储运, 2007, 26(2): 1-17.

[5] 邢静忠, 柳春图. 轴向力作用下埋设于线弹性土壤中的悬跨管道振动分析[J]. 工程力学, 2010, 27(3): 193-197.

[6] 邢静忠, 柳春图. 刚性土壤上含有轴向力的悬跨管道的静弯曲和固有频率[J]. 工程力学, 2011, 28(12): 87-91.

[7] 何 勇, 龚顺风, 金伟良. 考虑几何非线性的海底悬跨管道疲劳可靠性分析方法[J]. 振动工程学报, 2009, 22(3): 313-318.

[8] 黄和祥, 陈义厚, 彭玲玲. 气流管道系统振动原因及解决方案研究探讨[J]. 机械研究与应用, 2004, 17(5): 47-48.

[9] 徐 藏, 兰惠清, 何仁洋, 等. 悬索式管桥应变影响因素研究[J]. 石油化工设备, 2012, 41(3): 8-11.

[10] 胡家顺, 冯 新, 周 晶. 考虑边界土体性质悬跨管道振动特性分析[J]. 大连理工大学学报, 2010, 50(3): 409-415.

[11] Ai Shangmao, Sun Liping. The Effect of Functional Loads on Free Spanning Pipeline’s VIV Response [J]. Journal of Marine Science and Application, 2009(8): 151-155.

[12] Lottati I, Kornecki A. The Effect of an Elastic Foundation and of Dissipative Forces on the Stability of Fluid Conveying Pipes[J]. Journal of Sound and Vibration, 1986, 109(2): 327-338.

[13] 李 昕, 刘亚坤, 周 晶, 等. 海底悬跨管道动力响应的试验研究和数值模拟[J]. 工程力学, 2003, 20(2): 21-25.

[14] 李欣业, 张明路. 机械振动[M]. 北京: 清华大学出版社, 2009.

[15] 胡海岩. 机械振动基础[M]. 北京: 北京航空航天大学出版社, 2005.

Research on Longitudinal Vibration of the Spanning Pipe Undergoing Extrinsic Excitation

ZHAO Ming-ming1, XIONG Jin2

(1.LiaoheOilEngineeringConstructionSupervisionCo.,Ltd,PanjinLiaoning124010,China;2.JianghanPetroleumDrillCo.,Ltd,WuhanHubei430223,China)

Pipe is a carrier of the transportation of oil and gas, its performance is of great importance to the operation safety. Based on some reasonable assumptions, longitudinal vibrations responses of the spanning pipe are obtained by establishing mechanical model under vibration of the spanning pipe and by solving its differential equation of motion. The longitudinal amplitude of the pipe decreases with time when undergoing impulse load, this is primarily because of existence of damping. When undergoing general forces, response of the pipe can be treated as integration of the force function during the work time. The vibration amplitude of the spanning pipe with the action of harmonic force is related to the frequency ratio, the amplitude magnification coefficient is maximal when the external excitation frequency is close to the intrinsic frequency. The amplitude magnification coefficient decreases with increasing of the frequency ratio when the external excitation frequency is bigger than the intrinsic frequency.

extrinsic excitation; spanning pipe; longitudinal vibration; damping; frequency

2013-12-06

赵明明 (1986-)，男，辽宁丹东人，助理工程师，主要从事石油化工类工程建设方面的研究工作。

TH113.1

A

1007-4414(2014)01-0085-03