细长压杆失稳时最大挠度的确定*
董冠文, 李宗义, 赵彦军, 黄建明, 王泽荫,杨 龙, 张庆华, 杜建霞, 赵典凯
(甘肃机电职业技术学院,甘肃 天水 741001)
细长压杆失稳时最大挠度的确定*
董冠文, 李宗义, 赵彦军, 黄建明, 王泽荫,杨 龙, 张庆华, 杜建霞, 赵典凯
(甘肃机电职业技术学院,甘肃 天水 741001)
针对国内工程力学教材普遍认为细长压杆失稳变形挠曲线线性化方程中的挠度值不确定的错误观点,指出其对细长压杆失稳变形挠曲线线性化方程推导存在误区,以两端铰支细长压杆为例,建立了其失稳变形挠曲线线性化方程后,又考虑了压杆失稳后两端截面形心产生轴向位移参数,通过消参,确定了细长压杆失稳时最大挠度值。结果表明:压杆失稳后两端截面形心产生轴向位移以及临界压力的确定这两个条件缺一不可才能在线性化下确定细长压杆失稳时最大挠度值,挠度值的大小与轴向压力直接有关。
失稳变形;线性化;挠曲线
1 引 言
1744年,Euler首次提出了细长压杆失稳变形的弹性曲线问题,并用椭圆积分表示了细长压杆失稳变形挠曲线方程的精确解[1]。由于压杆失稳会导致整个结构的毁坏,因此保证结构及其杆件的稳定在工程技术中有重大意义。这就是压杆失稳变形理论目前应用在许多领域的原因。例如,宇宙飞船的推进器各级之间的连接杆及机器人手臂[2],冲裁凸模长度校核[17-18]等都是应用实例。由此可见,Euler的杰出贡献推动了力学的发展,并使力学在许多工程领域得到了广泛的应用。当其他人还在研究梁弯曲问题时,Euler提出了失稳(侧向弯曲)这个概念,不能不说是一个十分超前的贡献。
目前国内工程力学(含机械专业使用)教材在介绍压杆稳定这部分内容时,对Euler在1744年首次提出的细长压杆失稳变形挠曲线方程的精确解很少提及,主要原因是用这种精确解来计算要随时查阅椭圆积分表,给教学带来不便[13]。工程力学教材[3-7]采用了建立线性化的细长压杆失稳变形挠曲线方程的方法阐述细长压杆失稳问题。但这样做新的问题出现了,教材[3-7]认为细长压杆失稳变形挠曲线方程中的挠度值成了不确定的常数,可以成为任意值。一些学者撰文也认为细长压杆失稳本来就是其非线性力学行为造成的,用线性化理论近似处理一个原本为非线性问题是有局限的,因此线性化条件下不能确定挠曲线的挠度值[8-14]。
笔者以两端铰支细长压杆为例,建立了其失稳变形挠曲线线性化方程后,并考虑压杆失稳后两端截面形心产生轴向位移参数,通过消参最终首次确定了细长压杆失稳时最大挠度值。纠正了上述线性化的细长压杆失稳变形挠曲线方程不能确定挠度值的错误观点。
2 教材中压杆失稳变形挠曲线线性化方程推导的误区
一般教材都以图1两端铰支细长压杆失稳形态不考虑轴向位移,杆长是l,建立细长压杆失稳变形挠曲线线性化方程,得到挠曲线方程的通解为:
(1)

图1 两端铰支细长压杆失稳形态(不考虑轴向位移)
将左端边界条件x=0,w=0代入式(1)得:
B=0于是式(1)变为:
(2)
再将右端的边界条件x=l,w=0代入式(2)得:
(3)
A为不为0的常数(若A=0,w=0,不产生弯曲)
由式(3)得:
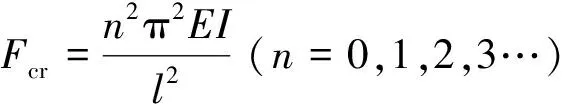
n=0时,w=0,不发生弯曲。n=1时,压力F为使两端铰支压杆发生未弯变形的最小力,即最小临界压力为:
临界压力对应弯曲变形为半个正弦波曲线
(4)
式(1)~(4)是文献[3]~[7]对细长压杆失稳变形挠曲线推导的过程,式(4)就是按照文献[3]~[7]观点推导得到的挠曲线方程。
(1) 误区之一:在式(1)~(4)文献[3]~[7]微弯条件下对细长压杆失稳变形挠曲线推导的过程中,可发现图1的挠曲线(挠曲线就是细长压杆侧向弯曲的形态,所以挠曲线长为l)在x轴投影长为l,违反投影规律。
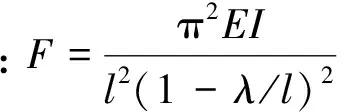
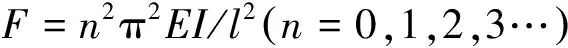
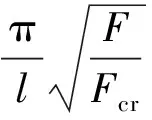
3 线性化细长压杆失稳变形挠曲线方程建立
为避免上述误区,如图2所示设两端铰支细长压杆长为l,等截面,材料均匀,承受轴向压力F的作用,轴向压力F严格作用在压杆截面的形心上。随着轴向压力F的增大,杆出现失稳现象,失稳后(侧向弯曲)的杆在x轴的投影长度恰好比杆本身长度l要短,此时压杆两端截面形心间产生了轴向位移,设其长度为λ,杆在x轴的投影长度为1-λ。代入将左端边界条件x=0,w=0,得到的方程仍然为式(2)。
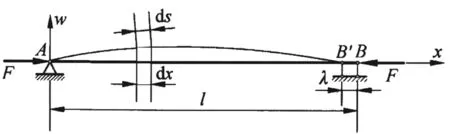
图2 两端铰支细长压杆失稳形态(考虑轴向位移)
3.1 直线平衡状态
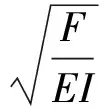
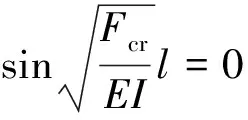
要使Fcr最小,只能取n=1,于是最终得出:
(5)
3.2 微弯平衡状态
因为刚度EI是常数,由最小临界值变形得:
(6)
代入挠曲线方程式(2)得:
(7)
取一阶导数得:
(8)
下面再求图2中的λ值,如图3所示。
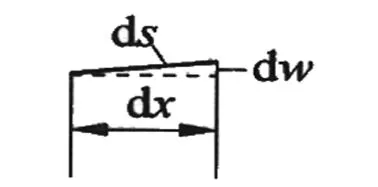
图3 从图2中的挠曲线取出长为ds的微段
设沿挠曲线取一长为ds的微段如图3所示,该段在x轴的投影为dx,于是有:
(9)
(10)
将式(8)代入式(10),同时将式(10)代入式(9)
(11)
代入挠曲线式(7)得:
(12)
代将式(11)代入式(12)后,再将式(5)代入得最大挠度为:
于是挠曲线方程为:
(13)
4 扰动对稳定性的影响
将其他状态下的临界压力:
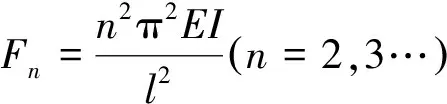
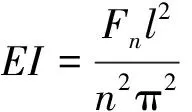
(14)
在与前面同样的假设条件下,对压杆施加扰动,要考虑纵-横弯曲方程即:
(15)
现在对方程式(14)改写为:
将上式代入式(15)得:
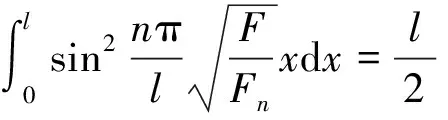
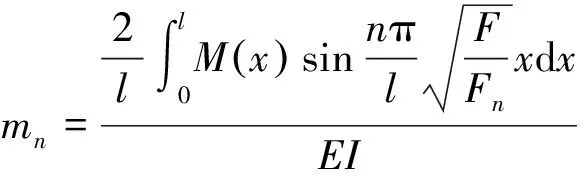
这里Fn是编号为n的临界力,得到挠曲线的表达式:
(16)
(17)
式(17)说明不论扰动mn多么小,当F=Fn时挠度趋于无限大。事实上,将EI=Fnl2/n2π2代入式(16),挠度恒为无限大,即平衡路径不存在,所以只有最小临界力才具有实际意义。
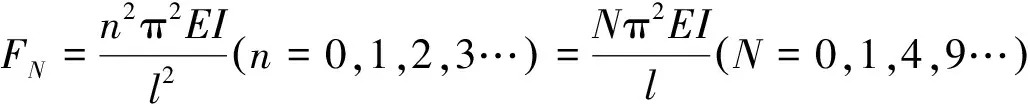
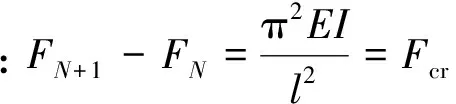
也就是说当FN 压杆失稳后两端截面形心产生轴向位移以及临界压力的确定这两个条件缺一不可才能在线性化下确定细长压杆失稳时最大挠度值,挠度值的大小与轴向压力直接有关。在机械工程中,一些设备的杆件结构不稳定导致产生挠曲线,不单纯是由于轴向压力大于最小临界力造成的,同时也与轴向压力大小是否保持在杆直线形态的范围有关。 [1] 纳什W A.[美]. 赵志刚译.材料力学[M].北京:科学出版社,2002. [2] 李世荣,孙 云,刘 平. 关于Euler-Bernoulli梁几何非线方程的讨论 [J]. 力学与实践2013,35(2):77-80. [3] 宋 曦,赵永刚,马连生. 材料力学[M]. 北京:科学出版社,2010. [4] 苏翼林.材料力学[M].天津:天津大学出版社,2001. [5] 单辉祖.材料力学问题的例题与分析方法[M]. 北京:高等教育出版社,2006. [6] 北京科技大学,东北大学.工程力学与材料力学合订版(第4版)[M].北京:高等教育出版社,2008. [7] 殷有泉,邓成光. 材料力学[M]. 北京:北京大学出版社,1992. [8] 张仲毅.细长压杆临界挠度确定性的简单解释[J]. 力学与实践,1992,14(5):60-62. [9] 张仲毅.对细长压杆临界挠度确定性的简单解释结果的改进[J]. 力学与实践,1996,18(8):60-63. [10] 张仲毅.临界压力下压杆挠度的分析与讨论[J]. 力学与实践,1995,17(4):73-74. [11] 薛福林.谈细长压杆稳定性问题[J]. 力学与实践,1995,17(5):65-66. [12] 梁枢平,邹时智.谈细长压杆稳定性问题[J]. 力学与实践,1997,19(4):67-69. [13] 吴 晓.细长压杆大挠度问题非线性振动比拟[J]. 力学与实践,1997,19(2):71-72. [14] 陈占清,孙明贵,李天诊.从非线性动力学的视角认识细长压杆的稳定性[J]. 力学与实践,2005,27(2):40-43. [15] 陈家骏.关于细长压杆稳定问题的注记[J]. 力学与实践,1994,16(1):62. [16] 陈家骏.关于细长压杆稳定性问题的讨论[J]. 力学与实践,1997,19(5):65-67. [17] 李宗义.非封闭形孔冲裁的受力分析[J].制造业自动化,2012,34(9):37-40. [18] 董冠文.冲裁凸模抗压弯能力校核的探讨[J].模具工业,2010,36(7):31-36. The Maximum Deflection Determination of Instability for Slender Columns DONG Guan-wen, LI Zong-yi, ZHAO Yan-jun, HUANG Jian-ming, WANG Ze-yin,YANG Long, ZHANG qing-hua, DU Jian-xia, Zhao Dian-kai (GansuMechanical&ElectricalVocationalCollege,TianshuiGansu741001,China) Engineering mechanics teaching materials in domestic are generally accepted the fault idea that the deflection value of slender compressive bar buckling deformation flexural linearization equation is uncertain, the auther points out the buckling of slender compressive bar deformation flexural linearization equation is derived incorrectly. Taking both ends hinged slender compressive bars as an example, after established its flexural buckling deformation linearization equation, and then considering axial displacement parameters compressive bar instability on both ends of the central section, through eliminating the parameter, the maximum deflection of instability slender compressive bar is determined. Results show that axial displacement of the compressive bar instability on both ends of the central section and the critical pressure have necessary conditions to determine the maximum deflection value of slender compressive bar under the linear instability, the deflection value is directly related with the size of the axial pressure. buckling deformation; linearization; flexural 2013-11-26 董冠文(1984-),男,甘肃天水人,助理讲师,主要从事模具结构力学方面的教学工作。 O341 A 1007-4414(2014)01-0015-045 结 语

