摩托车防护板有限元分析及其优化研究*
邓志强,彭卓凯,刘楹樾
(大长江集团有限公司, 广东 江门 529000)
摩托车防护板有限元分析及其优化研究*
邓志强,彭卓凯,刘楹樾
(大长江集团有限公司, 广东 江门 529000)
针对摩托车二次补气管防护板底盘试验断裂问题,进行了模态分析,找出了产生共振的模态频率和振型。通过对防护板进行动力学响应分析,计算出了结构薄弱位置以及应力分布,并对防护板结构进行形貌优化,得到满足加工工艺的加肋方案,以提高模态频率避开共振。且通过模态试验和应变测试的方法,验证了优化结构的合理性,从而为振动疲劳断裂问题提供可行的解决思路。
有限元;优化;振动;强度;疲劳
1 引 言
优化设计以数学规划为理论基础,将设计问题的物理模型转化为数学模型,运用最优化数学理论,以计算机和应用软件为工具,在充分考虑多种设计约束的前提下寻求满足预定目标的最佳设计。有限元法被广泛应用于结构分析中,采用该方法,任意复杂问题都可通过他们的结构响应进行研究。最优化技术与有限元法结合产生的结构优化技术逐渐发展成熟,并成功地应用于产品设计的个阶段[1]。
市场反馈的断裂问题或者试验中发现的断裂问题,通过分析计算和实验,能找到模型的薄弱部位,但是要如何解决断裂问题,尤其是振动疲劳断裂问题。一些机械部件由于高频振动而引起的断裂问题,只是单纯的加强薄弱部位,或改变薄弱部位的结构,多数情况很难对策到位,因此需要对模型的振动频率和振型进行分析,并进行相应的动力学分析,结合结构优化,以寻求最节省成本的解决方案。笔者将通过一个典型的模型摩托车二次补气管防护板,对此类问题进行阐述,为解决振动疲劳断裂问题提供思路。
2 模态分析
如图1所示为防护板有限元模型,采用有限元软件对摩托车二次补气管防护板,进行模态分析。根据实际工况,约束防护板上三安装孔位置,计算防护板的模态,可得到前5阶模态频率如表1所列。

图1 防护板有限元模型

表1 防护板模态频率计算结果
由于小排量摩托车发动机转速为0~12 000 r/min,对应的第1阶模态频率为0~200 Hz,所以通常关注的频率段为0~200 Hz。由表1可看出,只有第1阶模态频率在关注的频率段范围内,因此只关注第1阶模态频率166.1 Hz,对应的模态振型如图2所示,主要是沿板面的法向运动。对应的第1阶应变能分布如图3所示。
防护板第1阶模态频率166.1 Hz,对应发动机转速为9 966 r/min,由于此转速是发动机高速运转时的转速,因此易造成防护板和发动机产生共振。

图2 防护板第1阶模态对应模态振型 图3 防护板第1阶模态应变能分布
3 动力学分析
通过模态计算,找到了防护板的共振频率为166.1 Hz,易和发动机产生共振。然后采用直接频率响应的方法分析防护板的强度,找出防护板的薄弱位置及应力值大小。计算频率为166.1 Hz,结构阻尼为0.06,在频率段为0~200 Hz内,进行直接频率响应分析应力分布云图如图4所示。
由图4可看出,最大应力出现在模型的翻边起始点处,对应的Von-Mises应力为221 MPa,该点随频率变化的Von-Mises应力曲线如图5所示。由于防护板的材料是Q195,其屈服极限为195 MPa,防护板最大应力已经超过了材料的屈服极限,极易发生振动疲劳断裂,因此需要对该结构的防护板进行优化。

图4 防护板在频率166.1Hz下直接频率响应分析的应力分布云图 图5 最大应力节点随频率变化的等效应力曲线(直接频率响应)
4 结构优化分析
结构优化是在保证产品达到某些性能目标并满足一定约束条件的前提下,通过改变某些设计变量,使产品的性能达到最期望的目标。结构优化主要包含拓扑优化、形貌优化、形状优化、尺寸优化。通常根据不同的优化目标,选择不同的优化方法。
笔者采用形貌优化的方法。形貌优化是一种形状最佳化的方法,即在板形结构中寻找最优的加强肋分布的概念设计方法,用于设计薄壁结构的强化压痕,在减轻结构重量的同时能满足强度、频率等要求。
4.1 优化目标的确定
对防护板断裂处按照动力学方法进行分析,确定了防护板最大应力部位及共振频率为166.1 Hz。由于防护板除自身重力外,不受外力作用,只是三安装孔被螺栓约束和发动机共振,产生疲劳破坏,因此改进方案目标是提高防护板一阶模态频率到200 Hz以上。如何提高模态频率,模态频率与哪些参数有关?用矩阵表示模态运动方程[2]:

(1)
(2)
(3)
将式(2)、(3)代入式(1)可得到:
(4)
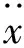
因此提高第一阶模态频率的方法是提高防护板的刚度或减少防护板的质量。防护板需要保护二次补气系统免受泥沙侵袭,故不能在上面打孔减少质量,只能提高防护板刚度来提高频率,但是摩托车二次补气管防护板要实现大批量生产,通过增加防护板板厚的方法提高刚度,这对成本的增加是不可估量的,因此在防护板上进行加筋,并对加筋的位置进行优化设计,以实现提高模态频率。
该方案的优化目标为保证质量基本不变,对三安装孔全约束,找出最佳的加筋区域,满足防护板第一阶频率最高。
4.2 形貌优化的设计变量与设计区域
采用形貌优化的方法,在防护板板形结构中寻找最优的加强肋,形貌优化的形状变量由参数(如最小肋宽、起肋角)确定,它们在形状上是圆形的,以近似的六边形分布在设计区域上,每个形状变量有一个圆形的中心区域,圆的直径等于最小肋宽。肋的最小宽度及起肋角决定形状变量的几何,最小宽度的推荐值为单元平均尺寸的1.5~2.5倍,这里设置为7 mm,起肋角推荐值为60°~ 75°,这里设置为60°。
设计区域是允许设计变量在这部分区域进行优化的区域,如果一个网格同属于几个设计区域,则它将成为每个设计区域形状变量的一部分。对于自动生成肋的变量,肋的拉伸高度根据网格所属肋的变量个数均分。防护板模型设计区域设置为除约束螺栓孔以外的所有防护板区域。
4.3 优化分析与结果分析
对模型如图1所示进行网格划分与设置材料属性,防护板材料为Q195,弹性模量为206 000 MPa,泊松比为0.3,密度为7.8×103kg/m3,板厚度为2 mm,壳单元为25 809个。
优化结果如图6所示,中间区域及靠近缺口处突起部分为可加筋的位置(图6中间凸起区域),按照图示位置加筋可达到第1阶模态频率最高为232 Hz。
由于优化得到的加强筋的边缘很不规则,工艺性差,故需要对优化得到的模型进行适当处理,得到如图7所示的3D模型。经过处理后的方案,第1阶模态频率为206 Hz,满足预期的优化目标。

图6 软件优化加筋的防护板方案 图7 优化后防护板方案
5 试验验证及结果分析
由于防护板是在底盘耐久试验台上出现断裂,因此需要对计算分析得到的模型进行验证,进行模态试验,并在底盘上对优化前后的防护板进行应力测试。
用锤击法把防护板安装在整车上,在防护板上布置多个加速度传感器,用力锤分别对修改前后的防护板根部进行敲击,得到防护板的第1阶模态频率如表2所列。
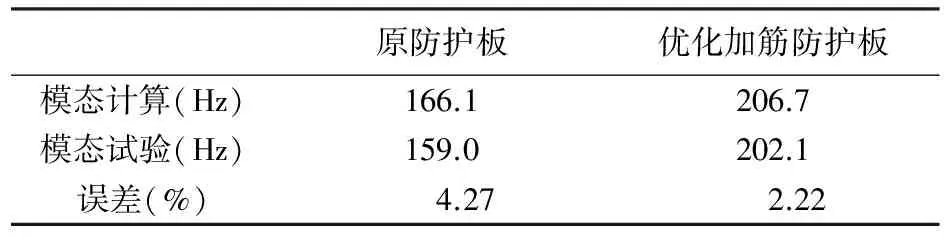
表2 防护板优化前后的第1阶模态频率对比
从表2可看出,计算和试验误差在5%以内,两者基本吻合。但计算通常较试验结果偏高,主要原因是加载的是固定约束,较实际约束刚度大。
优化加筋后的防护板,第一阶模态频率为202.1 Hz,对应发动机转速为12 126 r/min,由于发动机最高转速为12 000 r/min,因此避开了共振频率。
把修改前后的防护板安装在整车上,然后在底盘试验台上进行应力测试。测试的应变片布置在应力可能最大的部位,粘贴位置如图8所示。得到如表3所列的应力测试结果。

表3 防护板优化前后应力测试结果对比

图8 应变片粘贴位置示意分布图
由表3的测试结果可看出,2点为原防护板的薄弱位置,应力最大为221 MPa,优化加筋的防护板应力已经很小,因此计算优化分析得到的模型满足强度要求。并且该优化方案的防护板已经应用到新开发的车型中,通过各项疲劳耐久试验,未出现异常。
6 结 语
根据断裂位置及工况分析,确定优化目标提高防护板的第一阶模态频率。然后分析得到第一阶模态频率最高的优化模型,根据加工工艺需要,适当修改得到易于加工的设计方案。整个过程是分析优化并改进防护板的总体思路。
对于振动疲劳断裂问题,通常由于涉及领域较多,计算起来边界很复杂[ 6]。通过一个典型的模型摩托车二次补气防护板进行动力学分析及优化,再进行试验验证结果的正确性,为复杂振动疲劳断裂问题提供思路。
[1] 张胜兰,郑冬黎. 基于Hyperworks的结构优化设计技术[M]. 北京:机械工业出版社,2007.
[2] 庞 剑,何 华. 汽车噪声与振动—理论与应用[M].北京:北京理工出版社,2008.
[3] 谭加才,傅彩明,康颖安.基于虚拟样机立式电机有限元结构分析与优化[J].机械强度,2008,30(3):479-482.
[4] 姜元庆,李 伟.MSC Nastran 动力学分析指南[M].北京:中国水利水电出版社,2012.
[5] 杨 剑,张 璞,陈火红.MD Nastran 有限元实例教程[M].北京:机械工业出版社,2007.
[6] Weibull W. Fatigue Testing and Analysis of Results[M].New York: Macmillan Company,1961.
Finite Element Analysis and Optimization Research of the Protection Board in Motorcycle
DENG Zhi-qiang,PENG Zhuo-kai,LIU Ying-yue
(DachangjiangGroupCo.,Ltd,JiangmenGuangdong529000,China)
To solve the vibration problem of second air hose in durability experiment for the motorcycle protection board, the modal analysis is carried out to find resonant frequency and resonant mode. And then the weak areas of the structure and the stress distribution are obtained by dynamic response analysis. After that the structure of protection board is optimized. The project with rib and good manufacturability is obtained, which is to increase modal frequency and avoid resonance. Furthermore, the results are verified by modal experiment and strain test. Thus the method provides feasible solutions to the problem of fatigue-broken due to vibration.
FEA; optimize; vibration; strength; fatigue
2013-12-02
邓志强(1981-),男,湖北蕲春人,工程师,主要从事汽车、摩托车CAE与NVH方面的分析研究工作。
TH123
A
1007-4414(2014)01-0009-03

