有限元分析在结构振动设计中的应用*

王 华，许江文

(中国电子科技集团公司 第十八研究所，天津 300384)

有限元分析在结构振动设计中的应用*

王 华，许江文

(中国电子科技集团公司 第十八研究所，天津 300384)

有限元法是近似求解一般连续域问题的数值方法。随着有限元技术的迅速发展，结构有限元与产品设计结合的越来越紧密。在设计出某振动夹具结构后，利用有限元法对其模态参数进行识别，并依据识别出的数据对其结构进行改进和优化，使其满足振动试验要求。

有限元法；模态；结构设计

0 引 言

随着现代工业的进步，许多产品朝着更大、更快、更轻和更安全可靠的方向发展，这样对产品的力学环境要求越来越严酷，仅仅依靠静强度理论进行结构设计已无法满足设计要求。在结构设计时必须考虑动态因素的影响，振动分析愈显重要。作为振动工程理论的一个重要分支，模态分析或实验模态分析为各种产品的结构设计和性能评估提供了一个强有力的工具，其可靠分析结构往往作为产品设计和性能评估的有效标准，而围绕其结果开展的各种动态设计方法更使模态分析成为结构设计的重要基础[1]。特别是有限元(FEM)技术的发展，为模态分析的应用创造了更为广阔的环境。

有限元法是近似求解一般连续域问题的数值方法，它最先应用于结构的应力分析。有限元法是与工程应用密切结合的，是直接为产品设计服务的，随着有限元理论的发展与完善，通用的有限元结构分析程序大量出现，如Ansys、Ideals、MSC等，笔者采用Ansys Workbench对振动结构进行动态分析[2]。

1 结构振动分析的有限元法

机械和结构中的振动有些对我们有利，有些对我们有害，因此，必须对振动体本身的振动特性以及它对外激励力的响应由明确的认识。振动要解决的问题主要有两个方面：一是寻求结构的固有频率和主振型；二是分析结构的动力响应特性。结构的固有频率和主振型只与结构的刚度特性和质量分布有关，因此，可用自由振动微分方程来分析[3]：

(1)

式中：M为质量矩阵；K为刚度矩阵。

各节点的动位移随时间的变化为：

(2)

消去sin (ωt+α)得：

KX-ω2MX=0

(3)

在数学中，这是广义特征值问题。若结构发生自由振动，它应当有非零解，有：

(4)

式(4)是关于ω2的高次代数方程，通常叫做多自由度体系自由振动频率方程，它求解的特征值和特征向量分别对应结构振动的固有频率和振型，它的次数等于结构的自由度数n。

2 振动结构设计

某型号导弹用元器件在工作中由于机翼振动，使其在工作中受到强烈振动，为模拟其实际受力，其安装夹具结构设计如图1所示，考虑到加工成本，同时为减轻结构重量，该振动夹具结构由底板、支柱和工作台面螺接而成。结构整体采用铝合金材料。

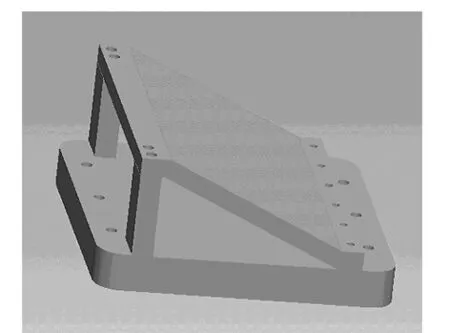
图1 振动夹具结构图

3 频响分析及结构改进

确定以上基本结构后，用Pro/E模，并导入Ansys有限元分析软件对该模型进行分析，根据分析结果不断改进完善设计模型。

3.1 结构有限元模型及频响分析

采用基于TGRID算法的四面体网格对其进行网格划分[4]，其有限元模型如图2所示，模态分析结果如表1,前三阶响应特性如图3～5所示。

表1 模态参数分析结果 /Hz

图2 有限元模型 图3 一阶响应

图4 二阶响应 图5 三阶响

从以上结果看，该结构的一阶共振频率为989.1 Hz，远小于试验条件的1 500 Hz，不能满足试验要求。

3.2 结构改进

为提高其一阶共振频率，将其结构中的两根支柱改为一整块支板，如图6，同上对其进行有限元分析，结果如表2、图7～9所示。从结果来看，改进后的一阶模态频率为1 415.7 Hz，接近试验技术要求的1 500 Hz，并且从图7和图3的比较中可以看出，改进后的一阶振型共振最大响应点位于夹具边上，避开了产品安装位置。大大降低了因共振引起的危险。

表2 改进后的夹具模态参数分析结果 /Hz

图6 改进后的夹具结构 图7 一阶响应

图8 二阶响应 图9 三阶响应

4 结 语

结构形状影响结构的动态特性，也就影响结构在动载荷下的传递特性。FEM在结构设计、应力分析中有着广泛应用，特别在设计中通过FEM法可以预先对结构进行理论分析，获得可靠的结构动态响应特性，及时优化改进，提高了设计的安全性和可靠性，避免生产中不必要的浪费，同时大大缩短设计周期。

[1] 曹树谦，张文德，萧龙翔.振动结构模态分析[M].天津： 天津大学出版社，2002.

[2] 郑术力，常少莉.振动试验夹具设计研究[J].装备环境工程，2006, 24(5)：14-18.

[3] 李景湧.有限元法[M].北京：北京邮电大学出版社，2002.

[4] 赵经文，王宏钰.结构有限元分析[M].北京：科学出版社，2001.

Application of Finite Element Analysis in Structural Vibration Design

WANG Hua, XU Jiang-wen

(The18thInstituteofChinaElectricalTechnologyCorporation,Tianjin300384,China)

The finite element method is the approximate numerical method for solving the general problem of the continuous domain. With the rapid development of finite element technology, finite element method and product design are combining more closely. In this article，a vibra- tion fixture structure is first designed, and then its modal parameters are identified by using the finite element method, and then its structure is improved and optimized to meet the requirements of the vibration test based on the identified data.

finite element method；modal；structure design

2014-02-14

王 华(1982-)，女，山西运城人，工程师，主要从事产品结构设计方面的研究工作。

TH122

A

1007-4414(2014)02-0107-02