3-DOF绳驱动并联机器人运动学建模及空间分析*

乔文刚，袁亭雪

(内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

3-DOF绳驱动并联机器人运动学建模及空间分析*

乔文刚，袁亭雪

(内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

研究并联机器人的结构参数与工作空间的关系。提出一种新型的三自由度绳驱动并联机器人，阐述并简化该机器人模型，在此基础上建立其正向运动学数学模型。利用数学工具Matlab对其工作空间进行仿真，结果表明该机器人的结构参数直接影响其工作空间，为机器人的结构开发奠定了理论基础。

绳驱动并联机器人；运动学；工作空间

0 引 言

工作空间是并联机器人一项重要性能指标，不同工况对机器人工作空间有着不同的要求[1]，故在设计过程中是一个不可回避的问题,也是实现并联机器人的充分利用的前提条件。因此，对工作空间形状和大小与并联机器人结构参数之间关系的分析是非常必要的。

笔者提出一种三自由度绳驱动并联机器人，所谓绳驱动是指机器人末端动平台的运动由柔性的绳进行驱动。它既具有并联机构的优点又具有绳索驱动的优点：①无需润滑：绳的柔性简化了关节的连接及润滑；②低惯性：材料提供最高的力/质量比,减小惯性，提高了机器人的响应速度；③工作空间大：柔性绳与摆杆连接处球关节比普通球关节活动范围大，使机器人具有更大工作空间[2]。

应用几何方法对该并联机器人进行分析，之后建立其正向运动学数学模型并求解。在此基础上用数学工具Matlab对其工作空间进行仿真分析。

1 三自由度绳驱动并联机器人模型

本文所述并联机器人采用Delta机构，该机构采用3组平行四边形机构。这种机构可以消除运动平台的转动自由度，而只保留空间3个平动自由度[3]。转动自由度的去除,使机构工作空间扩大,并减少了运动奇异点[4]。三自由度绳驱动并联机器人的三维型如图1所示。

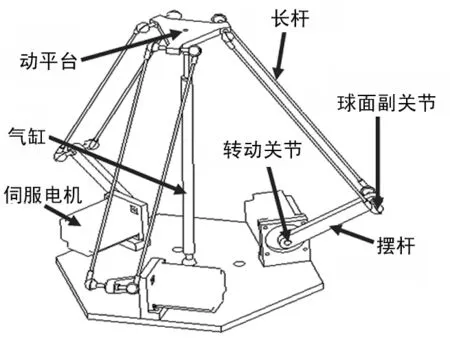
图1 三自由度绳驱动并联机器人

如图1所示，三自由度绳驱动并联机器人共计9个关节，包括3个转动关节(电机与摆杆的连接)和有6个球面副关节(绳与摆杆机、动平台的连接和气缸与上下平台的连接)。该机构的动力源来自安装在基座上的伺服电机，每个电机驱动一组摆杆和绳，绳的另一端与动平台相连。通过伺服电机输出的一定的转角带动摆杆使其摆动带动绳，从而使动平台实现预期的运动。绳只能承受张力,故在上下平台之间安装一气缸使绳时刻处于张紧状态， 同时利用气缸来作为支撑，使机构具有一定的刚度[5]。以动平台重力的1.5倍为气缸负载，确定其气压。

2 正向运动学数学建模

串联机器人的运动学正解很容易求得,而解析一般形式的并联机构的运动学正解迄今为止还没有得到解决，取而代之的是一些数值解法,典型的有非线性方程组消元搜索算法、神经网络算法等，这些解法可以得到精度令人满意的数值解,但在解决多解性问题及求解实时性方面存在不足。针对上述问题,笔者提出一种Delta 机构正运动学的几何解法. 相对于基于代数方程组的求解方法,其推导过程简单、直观,并能直接给出实时控制时满足连续运动条件的唯一解。

2.1 模型简化

将机器人模型首先进行简化。考虑到运动平台只有平动没有转动, Delta 机构中所有分支中的平行四边形框架始终为平面四边形,而不会扭曲为空间四边形[6]。在此条件下,平行四边形左右两边的运动与上下两边中点的连线的运动完全相同[7]。故将三自由度绳驱动并联机器人的模型进行简化化，如图2所示。

图2 简化模型及结构参数

如图2所示，该机器人的两个平台是两个等边三角形：上面的大三角形是装有电机的固定平台，3个电机之间的角度为120°；下面的小三角形是装有末端执行器的动平台。关节角度分别为θ1，θ2和θ3，点E0是末端执行器的中心，其坐标为(x0，y0，z0)。正运动学是以关节角度为已知参数，求解末端执行器中心的位置[8]，即建立以(θ1，θ2，θ3)为自变量，以(x0，y0，z0)为因变量的函数[9-10]。已知三自由度绳驱动机器人的结构参数，包括：f为固定平台三角形边长 (mm);e为末端动平台三角形边长 (mm);rf为固定平台连接杆长度 (mm);re为动平台杆的长度 (mm)。

2.2 建立正向运动学数学模型

选定固定三角平台的对称中心为参考坐标系原点，建立相应的坐标系，如图2所示，不难看出点E0的z0坐标值总是负值。

设三个球关节点分别为J1，J2，J3；固定三角平台三边转动中心分别为F1，F2，F3；移动三角平台三边的球关节点分别为E1，E2，E3。现在关节转角θ1，θ2和θ3已给定，需确定末端执行器中心点E0的坐标(x0，y0，z0)。由角度θ1，θ2和θ3可以确定点J1，J2，J3的坐标。臂J1E1,J2E2和J3E3可以分别绕点J1，J2和J3全空间自由旋转，形成三个以re为半径的球体。

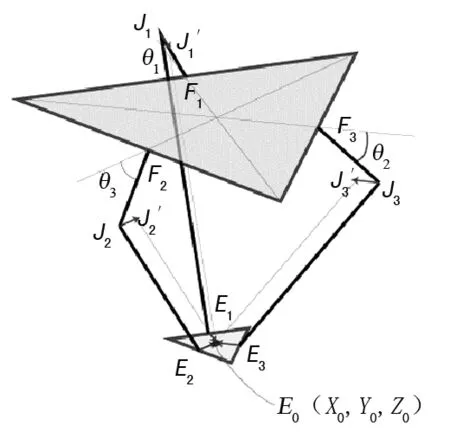
图3 正向运动学简化模型

图4 三自由度绳驱动并联机器人工作空间交集

所以要确定点E0的坐标(x0，y0，z0)，需要解决一组方程：

(1)

式中：i=1,2,3。球体中心坐标(xi，yi，zi)和半径re是已知的。

结合固定平台投影平面，如图5所示，不难得出：

FiJi=rf(cosθi) (i=1,2,3 )

图5 固定平台投影平面

式中：OFi为固定平台中心到三边转动中心距离；JiJi′为长臂的移动距离；FiJi为短臂投影到固定平台平面的长度。

可以确定点J1′，J2′和J3′的坐标为：

(2)

(i=1,2,3 )

将式(2)中J1，J2和J3的坐标分别代入球面方程式(1)，整理后得矩阵：

(3)

其中：

(4)

至此建立了三自由度绳驱动并联机器人的正向运动学数学模型并对其求解。对以上矩阵进行整理化简求得：

(5)

(6)

其中：

(z3-z1)(y2-y1)]

(7)

(8)

w1)(y2-y1)]

(9)

(10)

d=(y2-y1)x3-(y3-y1)x2

(11)

由矩阵式(5)和式(6)联合最终求得E0点坐标，由实际情况知z0应取最小负根。

(12)

由以上公式可以确定末端执行器中心点E0坐标，即确定了该机器人的工作空间，为下一步应用Matlab进行工作空间的分析提供理论依据。

3 工作空间仿真与分析

3.1 程序开发

在Matlab环境下进行三自由度绳驱动并联机器人工作空间的程序开发：首先使用meshgrid函数生成网格采样点，然后用Delaunay三角剖分算法将网格采样点平面剖分，同时对角度进行划分处理，最后使用tri三角表面绘图法进行工作空间描绘，输出三维图形[11]。具体程序流程如图6所示。

部分程序如下：[A,B]=meshgrid(linspace(0,1,n),linspace(0,1,n));%meshgrid:生成网格采样点函数A=reshape(A,prod(size(A)),1);%reshape:重新调整矩阵的行数、列数、维数B=reshape(B,prod(size(B)),1);%prod:求数组元素的乘积；size：返回数组的尺寸triAB=delaunay(A,B);%delaunay：三角剖分函数:

A = Xb(1)*ones(size(A)) + (Xb(2)-Xb(1))*A;

B = Xb(1)*ones(size(B)) + (Xb(2)-Xb(1))*B;

X = [ Xb(1)*ones(n^2,1) A B ; Xb(2)*ones(n^2,1) A B ;

A Xb(1)*ones(n^2,1) B ;

A Xb(2)*ones(n^2,1) B ;

A B Xb(1)*ones(n^2,1);

A B Xb(2)*ones(n^2,1)];……

图6 程序流程

3.2 程序正确性验证

以逆向运动学为理论基础，随机选取部分样点进行逆向运动学求解。输出的角度与工作空间程序要输入角度进行对比，来验证程序的正确性。逆向运动学输入的是动平台坐标如表1所列，输出的则是3个电机转动角度如表2所列。

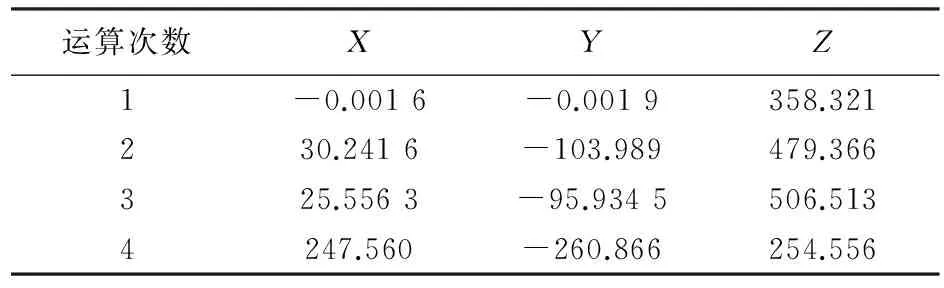
表1 动平台坐标输入 /mm

表2 角度输出 /rad

逆向运动学求解部分验证程序如下：

e=80;

f=400;

re=600;

rf=277;%机器人机构尺寸

y1=-0.5*0.57735*f;

y0=y0 - 0.5*0.57735*e;

a=(x0*x0 + y0*y0 + z0*z0 + rf*rf - re*re - y1*y1) / (2*z0); % 逆向角度求解1

b=(y1 - y0)/ z0; ……

3.3 实例仿真

在Matlab环境下采用三角表面绘图方法对3自由度绳驱动并联机器人进行仿真分析, 求出该机器人的最大工作空间, 其基本步骤为[12]:

(1) 选择一组确定的电机转动角度θ1，θ2，θ3；此文默认三个角度范围均为0°～90°。

(2) 输入一组机构设计参数f、rf、e和re。

(3) 选定一个动平台参考点O,将三个电机的转动角度θ1，θ2，θ3分别划分为N等份，每组角度对应与动平台参考点O的一组确定的位姿(x0，y0，z0)将求出动平台的每个位姿连接，绘制成三维工作空间图形输出。

(4) 重复步骤(2)和(3), 将机构设计参数输入，输出工作空间图形。(默认单位长度和角度都划分为100个单元)

针对图1所示的机器人机构模型, 选用表3所列的结构参数对机器人的工作空间进行仿真分析。 得出四组工作空间形状如图7所示。

表3 机构的设计参数 /mm

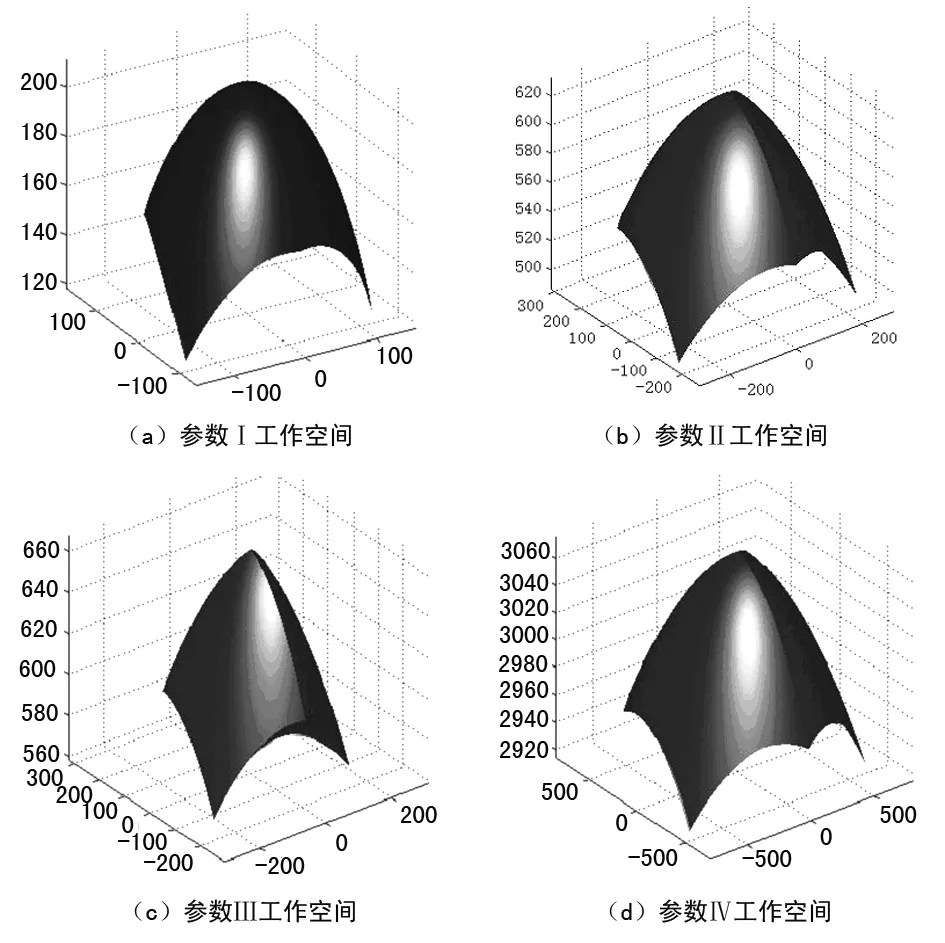
图7 三自由度绳驱动并联机器人工作空间

在开发程序过程中按照图1中模型动平台在上方，故图7中显示的工作空间z轴方向均为正值。

由于f、rf、e和re四个结构参数对机器人工作空间的影响是相互耦合的，故无法得出各个参数对工作空间定量的影响。只能对结构参数与工作空间之间关系进行定性分析。由图7可以看出：

(1) 动平台连接杆长度re对工作空间在z轴方向的最大值影响较大。

(2) 固定平台三角形边长f与其工作空间径向尺寸有关。

(3) 固定平台连接杆长度rf和电机转动角度θi将会影响机器人行程范围。

由以上分析可知，三自由度绳驱动并联机器人的结构参数直接影响其工作空间形状和大小。故可用逆向分析方法根据工作空间的仿真结果，确定机器人结构参数的大体范围。

4 结 论

对三自由度绳索驱动并联机器人模型进行简化, 建立正向运动学数学模型。然后对其工作空间进行仿真。Matlab三角表面法绘制的三维图形，可以更加直观展示其工作空间。分析结果验证了所述机器人正向运动学数学模型的正确性。根据实际工况，确定机器人的工作空间，进一步确定机器人结构参数的范围，为机器人的结构设计与改进奠定了理论基础。

[1] Kawamura S, Ito K. A New Type of Master Robot for Teleoperation Using a Radial Wire Drive System[C]. Intelligent Robots and Systems ′93, IROS ′93. Proceedings of the 1993 IEEE/RSJ International Conference on Intelligent Robots and Systems[A]. Yokohama, Japan, 1993:26-30.

[2] 郑亚青, 刘雄伟. 六自由度绳牵引并联机构的可达工作空间分析[J]. 华侨大学学报(自然科学版),2002, 23(4):393-398.

[3] 苏玉鑫, 魏 强, 段宝岩. 大射电望远镜精调Stew art平台工作空间分析[J].西安电子科技大学学报(自然科学版), 2003, 30(2):243-246.

[4] Ethan S, Vijay K. Workspaces of Cable Actuated Parallel Manipulators[J].Journal of Mechanical Design, 2006(128): 159-167.

[5] 刘雄伟，郑亚青.6自由度绳牵引并联机构的运动学分析[J].机械工程学报，2002(38)：16-20.

[6] 黄 真.空间机构学[M].北京：机械工业出版社，1991.

[7] 熊有伦.机器人学[M].北京：机械工业出版社，1996.

[8] 梁崇高，荣 辉.一种Stewart平台型机械手位移正解[J].机械工程学报，1991，27(2)：26-30.

[9] 赵 杰，朱延河，蔡鹤皋.Delta型并联机器人运动学正解几何解法[J].哈尔滨工业大学学报，2003，35(1)：25-27.

[10] 邢迪雄，张 琦.基于CATZAV5的工业机器人运动学仿真研究[J].机械，2011(1)：57-61.

[11] Hanselman D，Littlefield B. 张航，黄攀，译. 精通Matlab6 [M]. 北京：清华大学出版社，2002.

[12] Corke P I. A Robotics Toolbox for MATLAB[J]. IEEE Robotics and Automationg Magazine, 1996,3(1):24-32.

Kinematics Modeling and Work Space Analysis for Three-DOF Wire-driven Parallel Robot

QIAO Wen-gang, YUAN Ting-xue

(SchoolofMechanicalEngineering,InnerMongoliaUniversityofScienceandTechnology,BaotouInnerMongolia014010,China)

The relationship between structural parameters and workspace parallel robot for parallel robot is researched. A new three-DOF wire-driven parallel robot is proposed, the robot model is explained and simplified. Based on that, its forward kinematics mathematical model is established. Its workspace is simulated by mathematical tool Matlab. The results show that the structure parameters of the robot directly influence its workspace，which establishes the theoretical foundation for the development of robot structure.

wire-driven parallel robot; kinematics; workspace

2014-01-03

乔文刚(1961-)，男，内蒙古包头人，副教授，硕士，主要从事液压伺服与机器人等方面的研究工作。

TP24

A

1007-4414(2014)02-0043-05