离心压缩机蜗壳内部流动特性的数值研究*
刘震雄,胡 博
(1.上海民航职业技术学院,上海 200232; 2.上海飞机设计研究院, 上海 201210)
离心压缩机蜗壳内部流动特性的数值研究*
刘震雄1,胡 博2
(1.上海民航职业技术学院,上海 200232; 2.上海飞机设计研究院, 上海 201210)
针对蜗壳在提高离心压缩机整机效率中的重要性,利用数值模拟分析了非对称圆截面、对称圆截面和对称正方形截面3种不同结构形状的蜗壳内部的流动特性,重点研究了蜗壳结构形状对蜗壳内部的流动、静压、流量等参数的影响规律。综合比较3种结构蜗壳,非对称圆截面蜗壳最有利于流体在蜗壳流道内流动。
离心压缩机;蜗壳;流动特性;数值模拟
0 引 言
离心压缩机以其单级增压比高、稳定工作范围宽、结构简单可靠等优点广泛应用于航空航天动力系统,能源化工、汽车涡轮增压系统等方面。离心压缩机中的蜗壳用来收集来自叶轮的增压气流并引入排气管道,同时蜗壳也充分利用气流的动能进一步提高气体的压力[1-2]。蜗壳对于整个离心压缩机的效率及稳定工作都有很大的影响,因此有必要对蜗壳的内部流动进行深入研究。
针对离心压缩系统蜗壳内部的流动特性,国内外学者采用实验和数值模拟等手段进行了研究。刘伟,齐维彪,王尚锦[3]利用五孔探针对离心压缩机蜗壳内的三维流动进行了详细测量,了解其三维流动的生产演化细节,为蜗壳设计打下基础。Hagelstein D[4]针对对称矩形截面蜗壳进行了数值模拟研究,主要研究蜗壳内部的流动结构与损失,研究表明:流量的不同对蜗壳内部漩流结构的位置、通流速度、流动损失都产生一定的影响。张克松,王桂华等[5]通过CFD方法研究了蜗壳截面变化规律对蜗壳内部流动及出口参数的影响,通过对比分析,发现同一蜗壳在不同流向下,其出口速度及气流角的变化规律曲线基本相同,但绝对值随流量的降低而下降。周莉,张鑫[6]针对整机条件下的离心压缩机进行了详细的数值研究,分析了流量变化对蜗壳内的流动及压力的影响,计算结果表明随着流量的增加,蜗壳各截面中心总压显著增加;在蜗壳的周向方向上,蜗舌附近涡量和气流角随流量的变化波动较大。
目前离心式压缩机最常用的蜗壳形式从蜗壳横截面形状上区分主要有矩形截面与圆形截面两种;从蜗壳结构上区分主要有对称性与非对称性两种。
虽然到目前为止对于离心压缩机蜗壳内部的流动特性研究较多,但大多都考虑气流流量的改变、叶轮与蜗壳的匹配、蜗舌等方面对其影响[7-9],专门针对不同结构形状的蜗壳内部流动的研究还很少见,笔者利用数值模拟的研究方法,针对不同结构形状的离心压缩机蜗壳进行研究,重点分析蜗壳截面形状、蜗壳对称性对蜗壳内部流动的影响以及变化趋势,有助于离心压缩机蜗壳的选型,提高整机的性能,节约成本。
1 物理模型和计算方法
1.1 物理模型
笔者计算采用3种不同结构的蜗壳进行内部流动研究,即对称圆截面蜗壳、非对称圆截面蜗壳和对称正方形截面蜗壳。
蜗壳3维示意图如图1所示。蜗壳2维示意图如图2所示,其中θ为蜗壳周向角。
计算中采用的蜗壳截面面积沿周向角的变化规律基本相同,具体如图3所示。
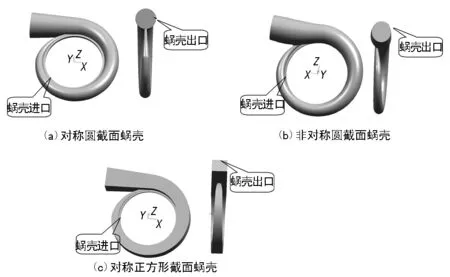
图1 蜗壳3维示意图

图2 蜗壳二维示意图
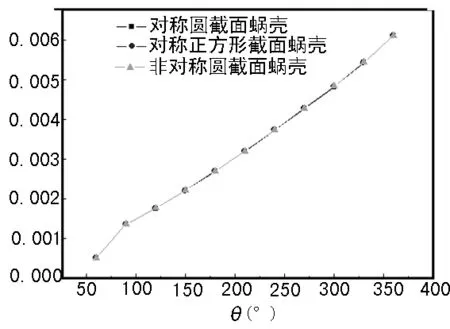
图3 蜗壳截面面积沿周向角的变化规律
1.2 网格划分和计算模型
数值模拟过程中,计算结果的准确与否同计算模型网格的划分和生成直接相关。笔者蜗壳模型网格划分采用分块技术,整个计算区域生成非结构化六面体网格,并且对蜗壳壁面进行网格加密处理。在计算之前,为保证计算结果的可靠性,进行了网格无关性计算。网格数量从36万增加到85万,从图4可看出,当网格数目增加到70万时,以蜗壳270°周向角截面处的面平均总压为参考量,基本没有变化,此时可认为数值计算结果与网格数目无关。
笔者计算采用商用软件ANSYS CFX,湍流模型采用标准k-ε双方程湍流模型进行计算,文献[6]和[10]的研究结果验证了采用标准k-ε湍流模型对离心蜗壳内流动模拟的可靠性。计算结果收敛的标准是各变量残差小于1×10- 5。
实际蜗壳内的流动受到上游叶轮、扩压器的影响,蜗壳进口呈现出周向非均匀性的特点。考虑到该项重点研究蜗壳的截面形状、对称性对蜗壳内部流场的影响,因此暂不引入周向非均匀的作用。蜗壳进口边界条件设为总压进口,出口边界条件为静压出口,壁面采用绝热、无滑移条件,流体采用理想气体。

图4 网格无关性实验图
2 计算结果分析
2.1 蜗壳结构对流场的影响
图5所示给出了3种蜗壳在90°、180°、270°、360°周向角截面处的速度流线图。从图中可看出,三种蜗壳内都存在明显的漩涡流动。在对称蜗壳截面内,如图 5(a)、(b)所示,在流场中存在一对旋转方向相反的对转漩涡结构,而在图5(c)中,在蜗壳截面内只存在一个明显的漩涡结构。
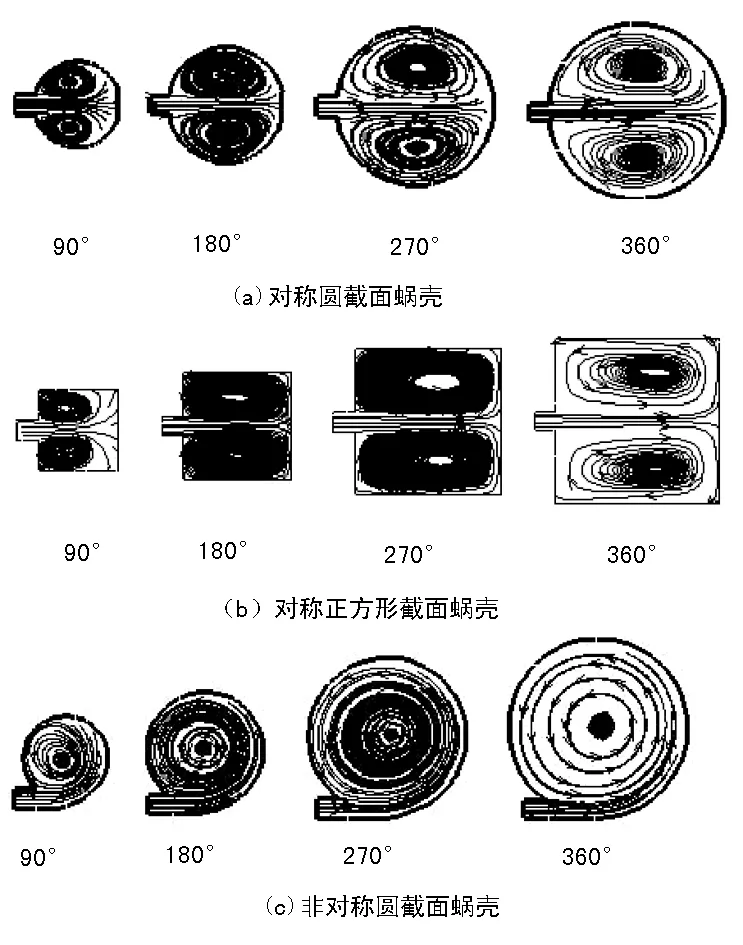
图5 蜗壳不同位置截面流线图
蜗壳内部不同的漩涡结构主要受到蜗壳进口径向速度和蜗壳截面形状的影响。在对称蜗壳内,流体径向流入蜗壳,受到蜗壳壁面约束速度降低,同时蜗壳为对称形状,流体沿蜗壳壁面均匀分流,对称的分成两部分。受壁面剪切力的影响,速度降低,静压升高,在蜗壳截面中心两侧形成低压区,流体在压力梯度的作用下,不断的从高压区域运动到低压区域形成一对旋转方向相反的漩涡结构,蜗壳截面的对称性导致蜗壳内的流场基本为对称的。
在非对称蜗壳中,气流切向流入蜗壳,在蜗壳的起始位置(周向角较小),在接近蜗舌附近,截面半径较小,流体充满流道,蜗壳内漩涡结构的形成主要受到壁面剪切力的影响,随着蜗壳周向角的增大,蜗壳径向速度增加,当下游径向速度更大的流体流入蜗壳流道包围在蜗壳内部已存在的流体外,漩涡结构自动形成。同时从图5也可发现,蜗壳截面内的漩涡结构随着通流面积的增大,漩涡的尺寸也逐渐扩大。
2.2 蜗壳结构对压力的影响
图6所示给出了计算工况下3种蜗壳内壁面静压分布云图。从图中可看出,沿蜗壳径向方向,静压随着径向距离的增大而增大,并在蜗壳外壁面处静压达到较大值;在蜗壳起始段,靠近蜗舌附近区域,流体外偏流入蜗壳,静压显著升高。比较图6(a)、(b)、(c),沿蜗壳壁面,非对称蜗壳的静压梯度变化小于对称蜗壳,在蜗舌附近非对称蜗壳的静压变化相对也较平缓,说明在蜗壳内部采用非对称蜗壳气流分布更加均匀,流动更容易。

图6 计算工况下蜗壳内壁面静压分布云图
图7给出了计算工况下3种蜗壳分别在90°、180°、270°、360°周向角处截面的静压分布云图。从静压云图发现,蜗壳外侧壁面压力较高,由外侧壁面向蜗壳内侧方向,压力呈降低趋势。
由于蜗壳通流速度和蜗壳环向半径在蜗壳内外壁面之间也形成了一个压力梯度,由式(1)确定。
(1)[11]
式中:VT为蜗壳截面通流速度,R为蜗壳环向半径。
因此从蜗壳流道内壁面向外壁面逐渐升高,高压区一直靠近蜗壳流道外壁面。
另一方面,在非对称蜗壳中,由漩流速度引起的离心力被从蜗壳截面中心到蜗壳壁面的压力梯度所平衡,由式(2)确定。
(2)[11]
式中:VS为蜗壳截面漩流速度,rc为涡流速度的曲率半径。
在非对称蜗壳截面中,压力从蜗壳流道外壁面向蜗壳流道截面中心逐渐降低,低压区在蜗壳流道中间,而高压区位于蜗壳流道外壁面。
在对称蜗壳中,气流正向进入蜗壳流道后直接冲击到蜗壳壁面上,气流速度急剧下降,动能转换为压力能,相对非对称蜗壳,蜗壳外壁面压力更高。
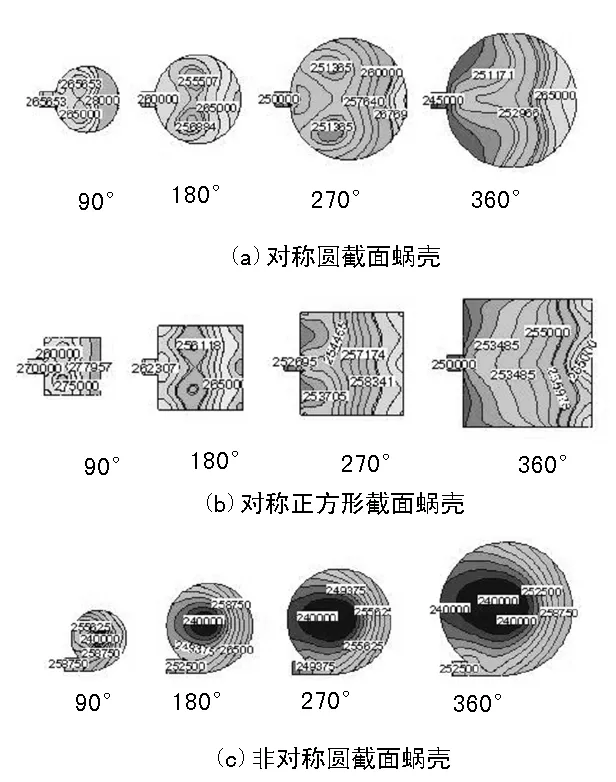
图7 蜗壳不同位置截面静压云图
图8给出了蜗壳不同周向角处截面的平均静压值曲线图。图中曲线表明,对称蜗壳的静压值明显高于非对称蜗壳的静压值,对称圆截面蜗壳与对称正方形截面蜗壳相比,静压值相差不大;在计算工况下,随着蜗壳周向角的增大,蜗壳截面静压都随之降低。
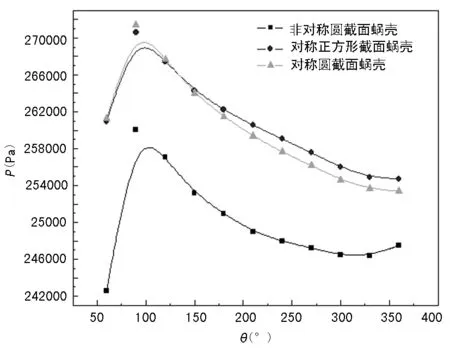
图8 蜗壳不同周向角截面平均静压曲线图
在本文计算工况中,3种蜗壳进、出口采用相同的边界条件,非对称蜗壳截面静压最小,结合蜗壳内部速度分析,表明在非对称蜗壳内部动能损失较小,相应的动压相对最大,流体在蜗壳流道中流动的动能较大,更加有利于流体流出蜗壳,而在对称蜗壳中,蜗壳内部的一对漩涡结构流动损失相对较大,流体流动动能相对较小,不利于流体流出蜗壳流道。
2.3 蜗壳结构对流量的影响
图9所示给出了计算工况下蜗壳截面单位质量流量沿蜗壳周向角θ的变化规律曲线图。
从图中可发现,蜗壳截面流量随着蜗壳周向角的增大而增大,且基本呈线性变化规律,说明在蜗壳模型计算中,流体在蜗壳流道中沿周向角的流动较均匀。从图中曲线也可发现,除了在蜗壳起始段位置,在蜗壳其他相同的截面位置,非对称圆截面蜗壳的单位质量流量最大,对称圆截面蜗壳次之,对称正方形截面蜗壳最小,结合前文关于蜗壳内速度和压力分析,说明采用切向进气的非对称圆截面蜗壳,流体在流道中流动阻力小,损耗低,流体更加容易流出蜗壳。
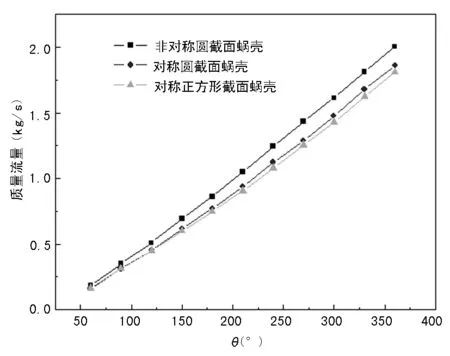
图9 蜗壳截面单位质量流量随周向角的分布曲线
3 结 论
利用数值计算的方法研究了3种不同压缩机蜗壳内部的流动特性。主要研究了不同蜗壳流量、内部速度、压力等变化的特点。得出如下结论。
(1) 受蜗壳进口径向速度和蜗壳截面形状的影响,在对称蜗壳截面内,存在一对旋转方向相反的漩涡结构;在非对称蜗壳截面内,只存在一个漩涡结构;
随着蜗壳通流截面积的增大漩涡尺寸增大。
(2) 蜗壳截面静压由外侧向内侧,呈降低趋势。在蜗壳靠近蜗舌附近,受流体外偏流进蜗壳的影响,静压显著升高。在计算工况下,随着蜗壳周向角的增大,蜗壳截面静压都随之降低且非对称蜗壳的静压值最小;对于对称结构的蜗壳,截面形状对静压的影响较小。
(3) 蜗壳截面流量随着蜗壳周向角的增大而增大,且基本呈线性变化规律;除蜗壳起始段位置,在蜗壳其他相同的截面位置,非对称圆截面蜗壳的单位质量流量最大。
(4) 就计算结果相比,非对称圆截面蜗壳对流动最有利。
[1] 冀春俊,王雅君,王学军,等.离心压缩机排气蜗壳内部流动分析与优化[J].机械工程学报,2009,45(5):312-317.
[2] 李 杜,杨 策,王一棣,等.涡轮增压器用离心压气机蜗壳流场计算研究[J].内燃机学报,2010,28(3):254-262.
[3] 刘 伟,齐维彪,王尚锦.离心压缩机圆形截面蜗壳内部三维流场的实验研究[J].流体机械,2006,34(11):1-5.
[4] Hagelstein D,VandenBraembussche R,Keiper R,et al.Experimental and Numerical Investigation of the Flow in a Centrifual Compressor Volute[J].Transactions of the ASME,Journal of Turbomachinery,2000(122):28-31.
[5] 张克松,王桂华,李国祥,等.蜗壳截面变化规律对蜗壳内流动及出口参数的影响[J].内燃机与动力装置,2009,112(4):20-24.
[6] 周 莉,张 鑫.离心压缩机蜗壳内部流动的研究[J].风机技术,2010(5):5-14.
[7] Steglich T, Kitzinger J, Seume J R. Improved Diffuser/Volute Combinations for Centrifugal Compressors[J].Journal of Turbomachinery,2008,130(011014):1-10.
[8] Semi Kim, Junyoung Park, Kukyoung Ahn.Improvement of the Performance of a Centrifugal Compressor by Modifying the Volute Inlet[J]. Fluids Eng,2010(132): 91-101.
[9] Chen Hua, Guo Strong. Numerical Simulations of Onset of Volute Stall Inside a Centrifugal Compressor . ASME Conf. Proc. 2008.
[10] 李安虎,李 红,刘炜巍,离心泵蜗壳内部流场的数值模拟[J].技术与应用,2004(11):50-53.
[11] 郭 强.带无叶扩压器的离心压缩机失速现象的实验和数值研究[D].上海:上海交通大学,2007.
Numerical Simulation of the Internal Flow in the Volute of Centrifugal Compressor
LIU Zhen-xiong, HU Bo
(1.ShanghaiCivilAviationCollege,Shanghai200240,China;2.ShanghaiAircraftDesignandResearchInstitute,Shanghai201210,China)
Numerical simulation was carried on three different centrifugal compressor volutes to study the effect of volute structure on the internal flow characteristics. The studies focus on the volute flow visualization, static pressure of the volute cross-section, mass flow in the volute and so on. Above all, the asymmetric circle cross-section volute was the most useful for fluid flowing in it.
centrifugal compressor; volute; flow characteristics; numerical simulation
2014-02-20
刘震雄(1981-),男,上海人,讲师,在读博士,主要从事叶轮机械方面的研究工作。
TK474.82
A
1007-4414(2014)02-0020-04

