码垛机器人动力学与控制分析*

赵 兴，贠 超，王 刚，朱鸿泰

(北京航空航天大学 机械工程及自动化学院，北京 100191)

码垛机器人动力学与控制分析*

赵 兴，贠 超，王 刚，朱鸿泰

(北京航空航天大学 机械工程及自动化学院，北京 100191)

MDJ90码垛机器人是一种用于完成生产线上物料搬运和码放的机器人。通过运用机器人的相关理论，对该机器人进行了运动学和动力学分析，并总结分析了该机器人的特点。在建立了基于拉格朗日方程的动力学模型基础上，对机器人采用了实时重力补偿的控制方案, 通过仿真实验表明了该方案的有效性。目前，相应的技术已经应用于机器人的现场作业中。

码垛机器人 动力学模型 实时重力补偿

0 引 言

随着工业自动化的发展，工厂的物流技术有了显著地提高，在物流大潮下，码垛技术便成为物流自动化技术领域的一门重要技术[1]。以此背景，码垛机器人以其在机械结构、适用范围、灵活性、成本以及维护等方面的优势，使其应用渐为广泛, 并成为一种发展趋势。

为了保证码垛机器人能平稳高速准确地运行，完成既定的工作要求，必须对机器人进行有效的控制。对机器人来说，控制的目的是要控制机器人手端的位置和姿态，即所谓位置控制问题。期望位置或轨迹可在机器人任务空间中给出，也可通过逆运动学关系转化为机器人关节空间中的期望轨迹，通常包括两种形式：一种是一个固定位置(定点)；另一种是一条随时间变化的轨迹[2]。此课题研究的码垛机器人在工作中只对抓取点和放置点有严格的位置要求，属于定点控制问题；但由于机器人负载重惯量大，为了保证运动的平稳流畅，则需可虑机器人的运动轨迹，即轨迹控制问题。

1 机器人动力学模型

为了对机器人进行有效的动态控制，首先需要建立其力学模型并进行性能分析。

1.1 码垛机器人的结构设计

码垛机器人MDJ90为四驱动关节，串并混联式结构，如图1所示。其中腰部关节实现底座1与腰部框架2的相对转动，水平滑块3与垂直滑块4分别实现机器人末端的前后与上下运动，腕部关节实现腕部框架10与抓手11的相对转动，同时利用辅助平行四边形结构8使机器人手端始终保持水平。

图1 码垛机器人简图1.基座 2.腰部框架 3.水平滑块 4.竖直滑块 5.大臂连杆 6.后大臂 7.前大臂 8.辅助平行四边形机构 9.小臂 10.腕部框架 11.抓手

1.2 机器人运动学分析

机器人采用4台交流伺服电机进行驱动如图2所示，其中腰部关节θ0和腕部关节θ3的回转决定了所搬运物料在水平面内的位置和姿态，垂直滑块和水平滑块运动带动臂杆的运动确定了物料在垂直面内的位置，将两部分分开进行讨论。

依次定义各臂长度:前大臂为l1，大臂连杆为l2，后大臂为l3，小臂为l4

首先分析臂部平行四杆机构的运动关系，随着垂直滑块和水平滑块的移动，当大臂和小臂分别从初始位置转动θ1和θ2后，这时根据几何关系可得腕部的位移ΔXp与ΔZp为：

相应的，也可得水平滑块的位移ΔX和垂直滑块

的位移ΔZ为：

如平行四边形机构满足如下比例关系：

则有：

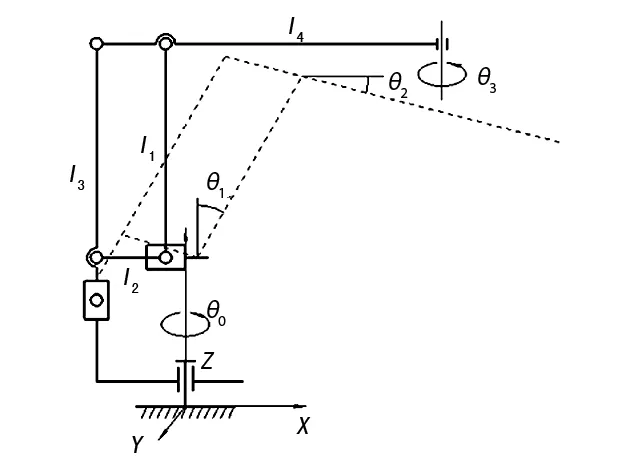
图2 码垛机器人臂杆机构运动图

这样，可知该机器人在垂直面内的运动上实现了解耦，为机器人末端轨迹的规划提供了便利，为机器人的轨迹控制提供了基础。

1.3 机器人动力学分析

(1) 广义坐标和广义力

由前面分析，大臂摆动角度取为θ1，小臂摆动角度为θ2，系统广义坐标即可描述该二自由度系统[3]。

该机器人的非保守力有

关节力矩为：

τ=[τ1,τ2]T

式中：τ1为驱动水平移动关节的电机输出力矩，τ2为驱动垂直移动关节的电机输出力矩。

τ对机器人的总需功为：

δW=τTδq=τ1δX+τ2δZ

根据几何关系有：

整理得，系统的广义力为：

(2) 四杆机构的拉格朗日方程

根据系统的拉格朗日方程：

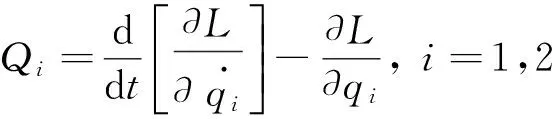
式中：L=T-U

首先应分别求出每根杆件的动能Ti和势能Vi。

对于前大臂(杆1)：

V1=m1gl1ccosθ1

对于大臂连杆(杆2)：

V2=m2gl2ccosθ2

对于后大臂(杆3)：

当杆2静止，杆3随杆1转动时有：

当杆1静止，杆3随杆2端点平移时有：

整理计算,得杆3的动能与势能为：

V3=(l2cosθ2+l3ccosθ1)m3g

同理，对于小臂(杆4)：

V4=(l1cosθ1-l4ccosθ2)m4g

设末端执行机构和负载m0，由于始终随小臂移动，与其有相近的动能和势能表达式：

V0=(l1cosθ1-l4ccosθ2)m0g

拉格朗日函数为：

L=T1+T2+T3+T4+T0-V1-V2-V3-T4-T0

代入拉格朗日方程，可得到系统的动力学方程:

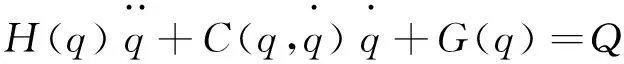
其中：

H12=(m3l3cl2-m4l4cl1-m0l4l1)cos (θ1-θ2)

H21=(m3l3cl2-m4l4cl1-m0l4l1)cos (θ1-θ2)

C12=(m3l3cl2-m4l4cl1-m0l4cl1)sin (θ1-θ2)

C21=(m3l3cl2-m4l4cl1-m0l4cl1)sin (θ1-θ2)

G11=(m1l1c+m3l3c+m4l1+m0l1)gsinθ1

G21=(m2l2c+m3l2-m4l4c-m0l4)gsinθ2

通过分析可清楚地看出，系统中所有由哥氏力引起的惯性力消失了，因而没有哥氏加速度的产生，只有惯性力、向心力和重力加速度，这样机构中臂杆之间的相对运动关系就变得相对简单，能够改善机器人的动态特性。

另外，在水平面内，各臂杆仅随腰座作回转运动，并将各构件看作集中质量的刚性元件，因此，腰座回转的广义驱动力矩为：

2 码垛机器人控制分析

当忽略重力和外加干扰时，采用独立的PD控制[4]，能够满足机器人定点控制的要求，其控制方程为：

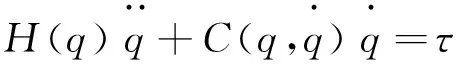
计算上式结果，整理得：

H(q)=

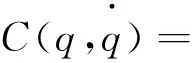
由于本码垛机器人惯量大、负载重，为了完整地描述机器人的动态特性则必须考虑重力，对机器人采用在线估计动力补偿[5]，此时控制方程变为：

整理上式，可得：

而且在实际中，由于动力学模型不可能绝对准确，并且系统中还存在干扰和噪声，仅采用开环控制是不实用的。构造高性能控制系统的可行方法是实时反馈控制，用关节传感器组成闭环系统，计算伺服误差，这时控制系框图如图3所示。

图3 机器人控制系统框图

可看出，该系统属于引入了进行实时重力补偿的内控制回路，属于考虑的机器人动力学性质的动态控制方案[6]。

此时控制方程为：

取运动过程中机器人某典型位置，θ1=30°，θ2=30°。

根据上述控制方程，进行计算机仿真，同时分别调整各环节Kd与Kp，得到相应的阶跃响应曲线，如图4所示。

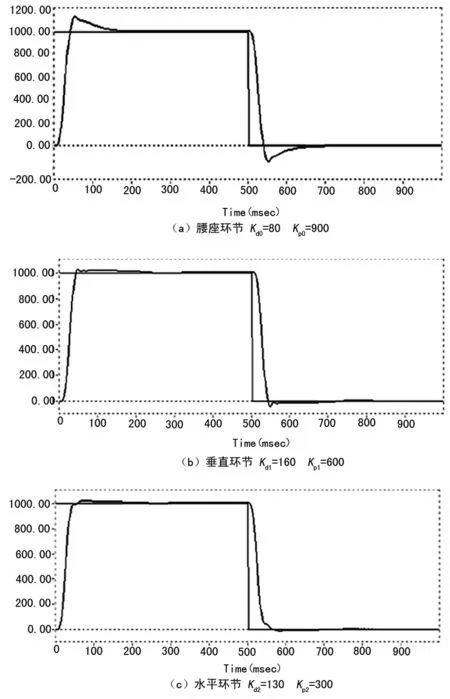
图4 控制系统阶跃响应曲线

从仿真结果可看到，采用本控制方案可得到较好的系统稳定性和瞬态响应。但是，为了得到较为理想的控制曲线，一方面要进行动力学的实时解算，另一方面也要根据机器人的运行状况，及时调整各环节的PID参数，对控制软件的算法编写提出了要求。

3 结 语

根据机器人理论分析了码垛机器人的运动学与动力学，然后根据建立的力学模型，分析了该机器人的运动特点与力学性能。在此基础上，分析了采取实时重力补偿的控制方案，并进行了计算机仿真，得到该方案可满足机器人的控制要求。同时，也对课题研究接下来的详细设计提供了参考，对控制器参数的调节与上下位机软件的算法编写等工作提出了基础。

[1] 胡洪国，高建华.码垛技术综述[J].组合机床与自动化加工技术，2000(6)：7-9.

[2] 熊有伦.机器人学[M].武汉：华中科技大学出版社，1996.

[3] 费仁元，张慧慧.机器人机械设计和分析[M].北京：北京工业大学出版社，1998.

[4] Craig J. Introduction to Robotics-Mechanics and Control[M].Reading, Assachusetts: Addison - Wesley Publishing Company, 1986.

[5] 丁学恭.机器人控制研究[M].杭州：浙江大学出版社，2006.

[6] 霍 伟.机器人动力学与控制[M].北京：高等教育出版社，2005.

Dynamics and Control Analysis of the Palletizer Robot

ZHAO Xing，YUN Chao，WANG Gang，ZHU Hong-tai

(CollegeofMechanicalEngineeringandAutomation，BeihangUniversity，Beijing100191，China)

The MDJ90 palletizer robot is used to transfer and palletize cargoes on the production line. Using robotics theory, the kinematics and dynamics of the robot are analyzed and summarized some feature. By the dynamics model based on Lagrange Equation, we take the control project of real-time compensation for the gravity and prove the validity of it by computer simulation. Now this technology has been applied to fieldwork of the palletizer robot.

palletizer robot；dynamics model；real-time compensation for the gravity

2014-03-10

赵 兴(1987-)，男，辽宁沈阳人，硕士，主要从事工业机器人结构设计与控制技术方面的研究工作。

TP242

A

1007-4414(2014)02-0008-03