带自控翼穿浪双体船纵向运动研究

刘 伟,侯国祥,许 晟,王永宁,杨 帅,吴启瑞

(1.华中科技大学 船舶与海洋工程学院，湖北 武汉 430074；2.中国舰船研究设计中心, 湖北 武汉 430064)

带自控翼穿浪双体船纵向运动研究

刘 伟1,侯国祥1,许 晟2,王永宁2,杨 帅2,吴启瑞2

(1.华中科技大学 船舶与海洋工程学院，湖北 武汉 430074；2.中国舰船研究设计中心, 湖北 武汉 430064)

减小穿浪双体船在波浪上的纵向运动对提高其性能具有非常重要的意义。本文在传统固定水翼和尾压浪板的基础上引入自控翼系统，根据切片理论，利用Matlab编程计算穿浪双体船的纵向运动。根据计算和试验结果分析得到水翼的最佳运动控制方式，进而得到穿浪双体船带自控翼时的纵向运动。对比结果表明，自控翼系统可以较大地减小穿浪双体船的纵摇幅值。

穿浪双体船;减摇效果;自控翼;切片理论

0 引 言

船舶在波浪中的运动性能是衡量其性能是否优良的一个重要标志，而纵向运动性能对穿浪型双体船来说尤为重要，过大的纵向运动幅值将严重损害船的航行性能指标。在双体船上设置前后稳定鳍[1-3]，不但能保证船的纵向运动稳定性，而且还能改进船在迎浪航行时的运动性能，进而消减船的纵向运动，减小其在波浪上运动的幅值。

为进一步改进穿浪双体船的纵向运动性能，必须对前后鳍施加控制，从而使鳍产生的升力和恢复力矩始终与波浪扰动力矩相反。通常需要设计一个反馈控制系统，根据设置在船上某些特定位置的传感器所测得的船运动的位移、速度和加速度信号，按一定规律对鳍的控制执行机构发出动作指令，控制鳍的运动，达到消减纵向运动的目的，这正是本文所要研究的自控翼系统。

1 基本理论

加水翼和尾压浪板控制后船的纵向运动方程为：

该方程是在微幅波及细长体理论假设下的二阶常微分方程组，表示船舶在微幅规则波中逆浪运动时纵摇和升沉的耦合运动。

由于水翼和尾压浪板的作用，原方程左边各水动力系数发生了变化，这些水动力系数由船运动引起的势流运动、粘性作用、水翼和尾压浪板的水动力效应组成。其中，势流引起的可按切片理论计算，粘性和鳍所产生的水动力系数是以试验和半经验半理论方法推出的[4-5]。

方程右边加进了由水翼和尾压浪板工作提供的恢复力和恢复力矩，其中Ff(t)为鳍升力所产生的恢复力，Mf(t)为鳍升力产生的力矩，用以抵消波浪扰动力矩，达到消减纵向运动的目的。

设水翼力矩导前纵摇运动的相位为εθf，纵摇滞后于波浪力矩的相位为εθw，则水翼的力矩为可表示为：

Mf(t)=Mfae-i(wet-εθw+εθf)。

其中纵摇滞后于波浪力矩相位εθw可由船的纵向运动方程组解得：

εθw=tan-1(-ξ5S/ξ5C)。

由于水翼和尾压浪板分别位于船的首尾部，为了使二者产生的力矩都能够抵消波浪干扰力矩，需要保持压浪板与水翼运动方向相反，即相位差始终为180°。因此问题的关键就是确定水翼力矩导前纵摇相位角εθf。当保持水翼的运动周期与船的遭遇周期相同时，水翼的转角可以设为

αf(t)=αfe-j(ωet-εθw+εθf)。

其中αf为水翼运动的幅值。

在小攻角下，鳍的升力可表示为：

式中：A(f)为水翼的投影面积；CLα为水翼的升力曲线斜率；ρ为水密度；U为船速。

假定水翼压力中心位于水翼导缘后1/4平均弦长与展长中线的交点(l,0,-d1(l))，不计船体和水翼对波的绕射效应，在小攻角假设下， 水翼压力点的攻角为：

当水翼的转角为αf(t)=αfe-j(ωet-εθw+εθf)，水翼压力点的攻角[6]为：

αf·e-j(ωet-εθw+εθf)。

水翼的惯性力可表达为：

水翼的横向粘性阻力可表达为：

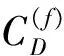
由水翼引起的纵摇力矩为：

则纵向运动由水翼引起的水动力系数和波浪扰动力为：

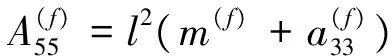
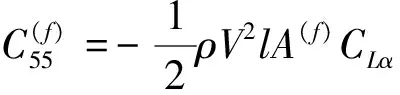
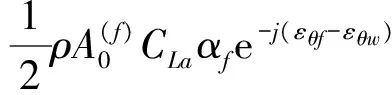
2 控制系统

2.1 系统布局情况

水翼和尾板位置如图1所示，水翼的构造以及尾板伺服机构如图2所示。控制过程中，主水翼固定，襟翼和尾板根据命令转动。控制系统设备布局情况如图3所示。

图1 水翼和尾板安装位置Fig.1 Installation location of hydrofoil and stern flap

图2 水翼和尾板结构Fig.2 Structure of hydrofoil and stern flap

图3 设备布置Fig.3 Equipment layout

2.2 系统工作原理

系统工作原理如图4所示，通过监控计算机接收并显示水翼艇当前的姿态、前水翼的转角、后尾板位置。然后可以由操作人员通过监控计算机下达前翼、后尾板的转角指令(遥控)，或根据控制程序自主控制并且准确定位(自控)。进而同步到控制器进行伺服控制，并将电机运动和编码器信息反馈到同步控制器。控制系统如图5所示。

图4 工作原理框图Fig.4 Working principle diagram

图5 控制系统框图Fig.5 Control system block diagram

3 水翼导前纵摇相位角研究

3.1 模型参数

文中研究的某穿浪双体船为WPC-X，船模与实船缩尺比是1∶25，船模主要尺度和参数如表1所示。

表1 WPC-X船模参数表Tab.1 Parameter table of WPC-X

3.2 程序可靠性验证

穿浪双体船WPC-X在迎浪状态下，实船航速35kn(Fn=0.597)，光体和带固定翼的纵摇运动幅值响应函数计算值与试验值的比较分别如图6和图7所示。从图中可以看出，计算和试验结果吻合较好，因此该程序能够较好地预报穿浪双体船的纵摇运动。

图6 WPC-X光体纵摇频响曲线比较Fig.6 Pitch frequency response curve of light body model

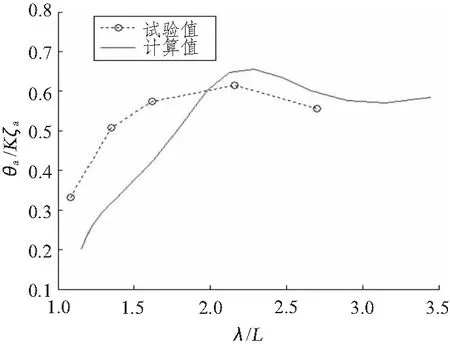
图7 WPC-X带固定翼纵摇频响曲线比较Fig.7 Pitch frequency response curve of WPC-X model with fixed wing

3.3 导前纵摇相位角研究

通过程序计算得到双体船在不同的导前纵摇相位角εθf时的纵摇运动如图8所示。

图8 计算得到的纵摇幅值与导前纵摇相位角关系Fig.8 Relationship between pitching amplitude and the phase angle ahead pitching by calculating

由计算结果可以看出，水翼运动导前纵摇相位角εθf=90°时能达到最好的减纵摇效果。而在实际问题中，由于控制系统在工作过程中存在一定的延迟问题，往往最佳的导前纵摇相位角是需要大于90°的。于是通过模型试验来探究最佳的导前纵摇相位角同时证明理论计算的可靠性。

图9 试验得到的纵摇幅值与导前纵摇相位角关系Fig.9 Relationship between pitching amplitude and the phase angle ahead pitching by tests

其中波长5m，水翼超前纵摇相位角0°和100°时的纵倾角度和水翼返回角度关系如图10和图11所示(图中幅值较小的为纵摇角度，较大的为水翼返回角度)。

图10 εθf=0°时纵摇角和水翼角度关系Fig.10 Relationship between pitching angle and hydrofoil angle when εθf=0°

图11 εθf=100°时纵摇角和水翼角度关系Fig.11 Relationship between pitching angle and hydrofoil angle when εθf=100°

从模型试验结果可看出，当设定的水翼转角导前纵摇相位角为100°左右时，实际水翼的转角刚好超前纵摇运动90°相位，此时的减纵摇效果最明显。因此在后面的试验中都将控制系统中的水翼导前纵摇相位角设为100°。

4 自控翼系统减纵摇效果比较

4.1 规则波结果

穿浪双体船WPC-X在迎浪状态下，实船航速35kn(Fn=0.597)，采用前述最佳导前纵摇相位角自控翼系统时的规则波纵摇计算与实验频响曲线如图12所示。图中计算值与实验值吻合较好，说明该程序不仅可以计算光体和带固定翼的状态，对带自控翼状态也有较好的计算精度。

WPC-X迎浪状态时，实船航速35 kn(Fn=0.597)，在规则波中试验得到的各状态纵摇幅值频响曲线如图13所示。

图12 WPC-X 带自控翼纵摇频响曲线比较Fig.12 Pitch frequency response curve of WPC-X model with automatic control flap

图13 规则波试验结果比较Fig.13 Comparing of regular wave test results

4.2 非规则波结果

WPC-X迎浪状态下，实船航速35 kn(Fn=0.597)，5级海况非规则波试验得到的各状态纵摇有义幅值及减摇效果如表2所示。

表2 纵摇角有义幅值对比表Tab.2 The comparison table of pitch angle amplitude

5 结 语

程序计算结果与模型试验的结果能较好地吻合，可以看出该程序不仅能够很好的预报穿浪双体船光体或加固定翼时的纵向运动，同时也能较好的模拟加自控翼后双体船的纵向运动。从试验和计算结果可以看出，自控翼系统能够较大幅度地降低穿浪双体船的纵摇幅值，在对纵向耐波性能要求较高的船上有很好的应用前景。

[1] 常进.带T型翼的穿浪船运动姿态控制系统研究[D].武汉：武汉理工大学，2012.

[2] 朱海烨.小水线面双体船稳定鳍优化设计研究[D].哈尔滨：哈尔滨工程大学，2007.

[3] 李元晖.小水线面双体船减摇鳍系统控制分析与初步设计[D].哈尔滨：哈尔滨工程大学，2006.

[4] 刘应忠，缪国平.船舶在波浪上的运动理论[M].上海：上海交通大学出版社，1987.

[5] LEE C M.Prediction of motion，stability，and wave loads of small-waterplane-area twin-hull ships[J].Trans.SNAME，1977，85:94-130.

[6] 蔡新功，李积德.加装减纵摇组合附体舰船运动预报[J] .水动力学研究与进展(A辑)，2003(2):25-32.

CAI Xin-gong，LI Ji-de.Prediction of motion of ships with built-up stabilizing appendage[J].Journal of Hydrodyn-amics(A series)，2003(2):25-32.

Research on longitudinal motion of WPC with automatic control flap

LIU Wei1,HOU Guo-xiang1,XU Sheng2,WANG Yong-ning2,YANG Shuai2,WU Qi-rui2

(1.School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074,China；2.China Ship Development and Design Center,Wuhan 430064,China)

To reduce the longitudinal motion in waves of wave piercing catamaran is very important for improving its performance. In this paper,automatic control flap system is introduced based on the traditional hydrofoil and stern flap. The Matlab program based on strip theory is written for calculating longitudinal motion of WPC. Optimal mode of motion of flap can be found according to the calculation and experiment analysis. Then the longitudinal motion of WPC with automatic control flap can be

. The comparison results show that, automatic control flap system can greatly reduce the pitching amplitude of WPC.

WPC；damping effect；automatic control flap；strip theory

2013-10-12；

2013-12-16

刘伟(1990-)，男，硕士研究生，研究方向为船舶与海洋结构物设计制造。

U661

A

1672-7649(2014)06-0026-05

10.3404/j.issn.1672-7649.2014.06.005