不同航速下船舶浅水摇荡运动规律

吴 晞，韩晓光，李宇辰

(海军陆战学院，广东 广州 510430)

不同航速下船舶浅水摇荡运动规律

吴 晞，韩晓光，李宇辰

(海军陆战学院，广东 广州 510430)

浅水效应是船舶安全操纵所需考虑的重要因素。本文采用三维势流理论，以某NPL型船模为例，分别对其在次浅水、浅水、超浅水3种不同相对水深条件下的纵摇和垂荡运动幅值响应情况进行计算，并对纵摇和垂荡运动随航速的变化规律进行总结。本文计算结果可作为船舶驾驶员判断是否发生浅水效应的参考依据。

浅水效应；三维势流理论；纵摇；垂荡

0 引 言

船舶在浅水中航行时，由于水深受限制，船底和水底之间的流速增大，并使一部分水流被挤向船的两边舷侧方向流动，从而使船两侧的流速增大；浅水时船周围的流场发生变化，船侧、船底的流速比深水时大，致使粘性阻力增加。同时，由于船底流速增加、压力降低，从而使船的吃水增加和船的航态发生变化[1]。

随着船舶大型化、高速化的发展，船舶的速度越来越快，吃水越来越深，相对的浅水域也就越来越多，船舶在港口附近或浅海发生触底、搁浅的概率不断增大。浅水效应是船舶安全操纵所需考虑的重要因素之一，对浅水域条件下船舶摇荡运动情况进行研究具有重要的现实意义。当前关于浅水域对船舶摇荡运动影响的研究并不多见，本文采用三维势流理论对某NPL型船在不同吃水、不同航速条件下的纵摇和垂荡运动进行计算，并对计算结果进行总结。

1 计算方法

1.1 三维势流理论

根据线性假设，船舶在波浪中的速度势按叠加原理可分为定常势和不定常势2部分。定常部分不考虑波浪影响，是船在静水中稳定到定常状态后的速度势，这部分速度势与时间无关，把它从总速度势中分离出来其余的非定常部分，记作ΦT(x,y,z)，速度势的分解如式(1)所示[2-3]：

Φ(x,y,z)=ΦS(x,y,z)+ΦT(x,y,z)。

(1)

式中：ΦS为定常势；ΦT为不定常势；ΦT可以分解为入射波势、辐射势和绕射势3部分，这样得到表达式(2)：

(2)

式中：ΦI为入射势；ΦR为辐射势；ΦD为绕射势；φ0为已知的入射波势；ω为波浪的遭遇频率；ηj为第j个运动模式的运动复幅值；φj为第j个运动模式单位幅值的摇荡运动的速度势。

1.2 速度势与流体力的求解

速度势所满足的条件如式(3)所示[4]：

(3)

[R]:远离物面的自由面上的波向后传播。

式中：n为物面上点的广义法向量；[L]为控制方程；[S]为物面条件；[F]为线性化的自由表面条件；[B]为底部条件；[R]为远方的辐射条件。

辐射势φj(j=1～6)和绕射势φ7可以通过三维源汇分布理论，采用边界元法求解，速度势可以表示为：

(4)

式中：σ为源强；S为入水结构面，(x,y,z)为流场中域点的坐标；(ξ,η,ζ)为S上源点的坐标；G为格林函数。

1.3 运动方程的建立

在随船平动坐标系下，利用微幅、线性化的假设条件，船舶在波浪中的运动响应X(ω)通过式(5)得到：[-ω2(Ms+Ma(ω))-iωC(ω)+K]X(ω)=F(ω)。

(5)

式中：MS为结构质量矩阵；Ma为附加质量矩阵；C为线性阻尼矩阵；K为系统刚度矩阵；F(ω)为波浪力。

1.4 频率响应函数

本文采用的频率响应函数定义如下：

(6)

式中：φa为纵摇幅值；za为垂荡幅值；ζa为波幅；ω为波浪圆频率。

2 计算模型

本文计算对象为NPL型船，模型的主要船型参数如表1所示。

表1 计算对象的主要参数

各站的剖面形状如图1所示。

图1 计算对象各站横剖面图Fig.1 The calculated object′s cross sections

前处理建模工具采用MAXSURF软件，水线以上部分和水线以下部分单独进行建模，计算对象建模后的三维效果如图2所示。

图2 计算对象三维模型Fig.2 The calculated object′s three-dimensional model

采用ICEM软件对计算模型进行网格划分，模型的网格划分效果如图3所示。

图3 计算对象网格划分结果Fig.3 The calculated object′s meshing result

3 计算结果及分析

考虑到计算对象在静水中正常排水条件下的吃水为2.226 m，当水深小于3倍船舶吃水时，浅水效应将会表现的比较明显[5-6]。本文分别对计算对象在顶浪航行条件下，运动速度分别为10 kn，15 kn，20 kn等3种情况，水深分别为4 m，6 m，8 m等3种条件下的垂荡和纵摇运动幅值响应函数进行计算，模型对象在浅水规则波下的波浪压力分布情况如图4所示[7-9]。

图4 船体表面波浪压力的分布情况Fig.4 The distribution of the hull surface wave pressure

分别对水深为4 m，6 m，8 m等3种水深条件下的纵摇运动与垂荡运动随航速的变化规律进行计算，计算结果如图5～图10所示。

3.1 不同航速下垂荡运动的变化规律

垂荡运动幅值响应函数随航速变化规律的计算结果如图5～图7所示。从图中不难发现，在3种不同水深条件下，波浪频率较低时，高速时的垂荡运动幅值响应要大于低速时的垂荡运动幅值响应，且水深值越大，垂荡响应幅值响应也越大；当波浪频率增大到一定值以后，低速时的垂荡运动幅值响应要大于但于高速时垂荡运动幅值响应，但这种高频率的波浪在实际环境下出现概率很小，且这种情况下的响应幅值也非常小，可以不予关注。

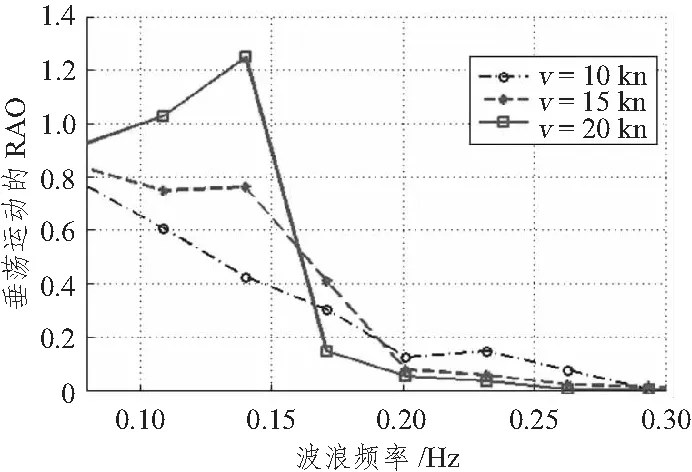
图5 不同航速下垂荡运动的RAO(h=4 m)Fig.5 The heave RAO in different speeds(h=4 m)

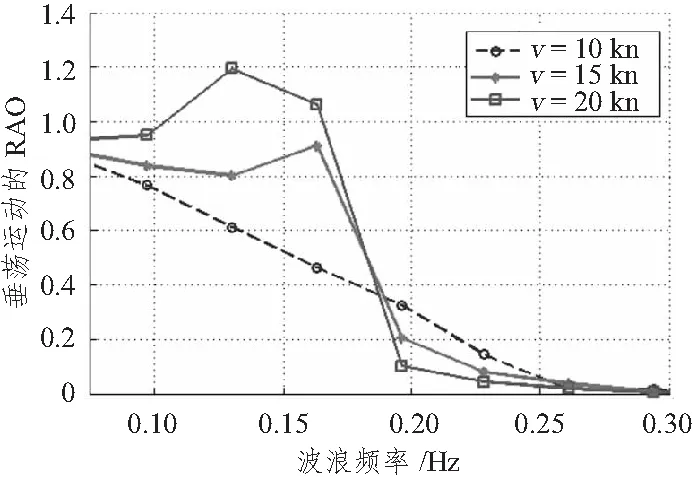
图6 不同航速下垂荡运动的RAO(h=6 m)Fig.6 The heave RAO in different speeds(h=6 m)

3.2 不同航速下纵摇运动的变化规律

纵摇运动幅值响应函数随航速变化规律的计算结果如图8～图10所示。在3种不同水深条件下，波浪频率较低时，高速时的纵摇运动幅值响应要大于低速时的纵摇运动幅值响应，且水深值越大，纵摇响应幅值响应也越大；当波浪频率增大到一定大小以后，低速时的纵摇运动幅值响应要大于但于高速时纵摇运动幅值响应，同垂荡情况相似，这种高频率的波浪在实际环境下出现概率很小，且高频波浪下的纵摇响应幅值也非常小，可以不予关注。

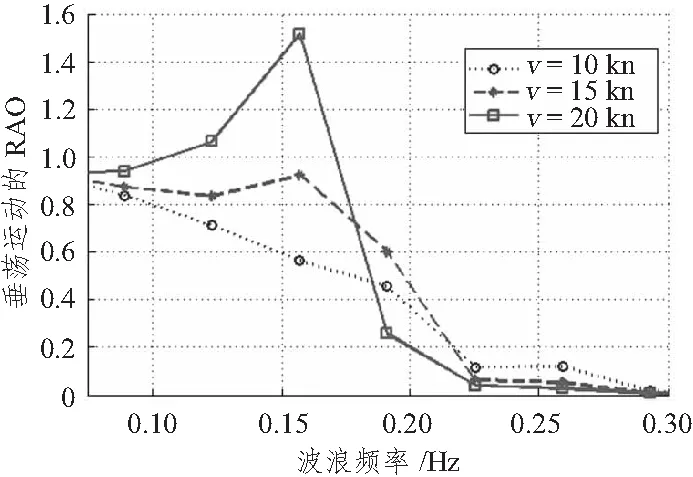
图7 不同航速下垂荡运动的RAO(h=8 m)Fig.7 The heave RAO in different speeds(h=8 m)

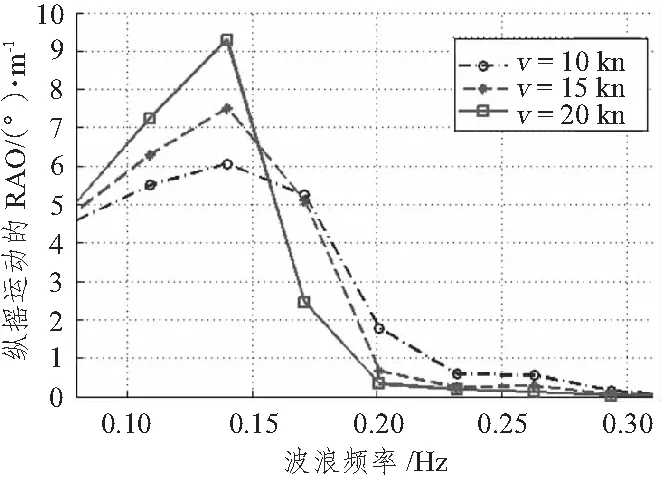
图8 不同航速下纵摇运动的RAO(h=4 m)Fig.8 The pitch RAO in different speeds(h=4 m)

图9 不同航速下纵摇运动的RAO(h=6 m)Fig.9 The pitch RAO in different speeds(h=6 m)

图10 不同航速下纵摇运动的RAO(h=8 m)Fig.10 The pitch RAO in different speeds(h=8 m)

4 结 语

本文应用三维势流理论计算了某NPL船型在浅水域条件下纵摇和垂荡运动的幅值响应函数。通过对计算结果分析可以发现，船舶在浅水中航行时应尽可能采用低速航行以免发生大幅摇荡；若采用同一航速航行在不同水深的水域，浅水时的摇荡幅值要小于深水条件下的情况，据此可以判断船舶是否发生浅水效应。

[1] 盛振邦，刘应中.船舶原理[M].上海：上海交通大学出版社，2003：293-304.

SHENG Zhen-bang,LIU Ying-zhong.Ship theory[M].Shanghai:Shanghai Jiaotong University Press,2003：293-304.

[2] 李积德.船舶耐波性[M].哈尔滨:哈尔滨工程大学出版社,2007.

LI Ji-de.Ship seakeeping[M].Harbin:Harbin Engineering University Press,2007.

[3] 戴遗山,段文洋.船舶在波浪中运动的势流理论[M].北京:国防工业出版社,2008.

DAI Yi-shan,DUAN Wen-yang.The potential flow theory of ship motion in waves[M].Beijing:National Defense

Industry Press,2008.

[4] 王献孚.船舶计算流体力学[M].上海:上海交通大学出版社,1999.

WANG Xian-fu.Ship computational fluid dynamics[M].Shanghai:Shanghai Jiaotong University Press,1999.

[5] 张显库,肖惟楚，郭晨.船舶进出港低速航向保持[J].交通运输工程学报，2005,12(4):77-81.

ZHANG Xian-ku,XIAO Wei-chu,GUO Chen.Course-keeping of inward-and-outward low speed ship[J].Journal of Traffic and Transportation Engineering,2005,12(4):77-81.

[6] 杨剑文.航行船舶在浅水中的纵倾变化研究[J].中国水运,2011,11(11):1-4.

YANG Jian-wen.Study on the change of inclination of ships in shallow water of the vertical[J].China Water Transport,2011,11(11):1-4.

[7] NOBLESSE F.Interal identities of potental theory of radition and diffraction of regular water waves by a body[J].Jour.Eng.Math.,1983,17:1-13.

[8] TELSTE J G,NOBLESSE F N.Numerical evaluation of the green function of water-wave radition and diffraction[J].Joural of Ship Research,1986,30(2):69-84.

[9] Ansys,Inc.AQWATM-LINE MANUAL[Z].2011.

Research on the law of ship shallow sway in different speed

WU Xi,HAN Xiao-guang,LI Yu-chen

(Navy Marine Academy，Guangzhou 510430,China)

Shallow water effect is the important factor of the ship manipulation safety. This paper use the three-dimensional potential flow theory to calculate an NPL model ship′s pitch and heave RAOs in different water depths, Summarize the pitch and heave variation motions with the speed.This paper evaluates can help ship pilots to judge whether the occurrence of shallow water effect reference.

shallow water effects;three-dimensional potential flow theory;pitching;heave

2013-04-22；

2014-05-15

吴晞(1958-)，男，教授，从事舰船操纵性与耐波性研究。

U661.321

A

1672-7649(2014)07-0024-04

10.3404/j.issn.1672-7649.2014.07.005