高速铁路桥上CRTSⅡ型板式无砟轨道温度荷载效应研究
李 伟
(中国铁道科学研究院研究生部,北京 100081)
我国高速铁路无砟轨道应用钢筋混凝土杆件“拉伸加劲效应”理论,通过设置连续底座板、“两布一膜”滑动层、“高强度挤塑板”等多项构造措施,实现了无砟道床的连续铺设[1-6]。桥上CRTSⅡ型板式无砟轨道系统梁轨相互作用的传力体系与既有的有砟轨道和单元板式无砟轨道线路的轨道结构受力变形特征有较大的不同。桥上无砟轨道结构跨梁缝连续铺设,使得梁跨间纵向连接刚度加大,在竖向活载和纵向活载作用下墩台、轨道结构受力分配有所不同。因此,在前期试验研究成果[7]的基础上,应对桥上CRTSⅡ型板式无砟轨道系统桥梁—轨道之间相互作用的受力变形特征进行深入的研究。
针对桥上CRTSⅡ型板式无砟轨道系统在季节温度荷载作用下的受力变形特征,本文采用ANSYS对32 m简支梁和(48+80+48)m连续梁(温度跨度128 m)进行数值分析,并选择相应工点对桥梁—轨道在温度荷载下的受力变形特征进行长期监测。
1 桥上CRTSⅡ型板式无砟轨道结构及受力分析
桥上CRTSⅡ型板式无砟轨道系统采用连续的轨道结构,并通过“两布一膜”滑动层与桥梁结构隔离,在桥梁固定支座部位设置剪力齿槽和锚固钢筋,使轨道结构的荷载向下部桥梁结构传递。桥上CRTSⅡ型板式无砟轨道由上至下主要由钢轨、弹性不分开式扣件、预制轨道板、水泥乳化沥青砂浆充填层、底座板、滑动层、高强度挤塑板、侧向挡块及弹性限位板等部分组成,桥台后路基设置端刺锚固结构(包括摩擦板、土工布和端刺)及过渡板。每孔梁固定支座上方设置剪力齿槽,梁缝处设置高强度挤塑板,底座板设置钢板连接器后浇带,如图1所示。
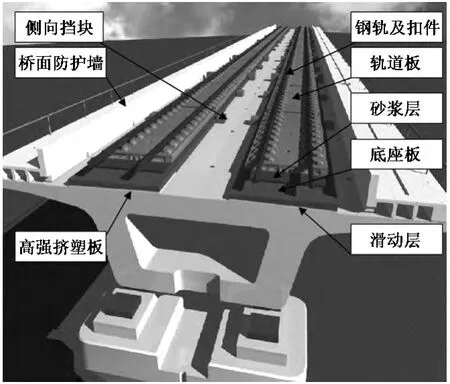
图1 桥上CRTSⅡ型板式无砟轨道示意
1.1 计算模型
桥上CRTSⅡ型板式无砟轨道是一个较为复杂的力学系统,其有限元计算模型的建立应在总体上较为真实地反映结构的受力,考虑计算方便和可靠性可进行适当简化。本文对桥上CRTSⅡ型板式无砟轨道系统的轨—板—桥—墩一体化模型作如下假定:
1)钢轨为纵向连续长梁,其拉、压刚度相等,钢轨按支承节点划分单元。
2)钢轨与轨道板间产生纵向相对位移,二者通过扣件相互作用,扣件阻力作用于钢轨节点与轨道板节点上。
3)砂浆层为轨道板和底座板提供非线性阻力作用,非线性阻力随着轨道板和底座板间的相对位移呈非线性变化。
4)底座板与桥梁间产生纵向相对位移,二者通过“两布一膜”滑动层与梁端剪力齿槽和锚固钢筋固结机构进行纵向相互作用,滑动层的摩擦阻力与二者间的相对位移为非线性关系,固结机构纵向作用力与二者间的相对位移为线性关系。
5)底座板与端刺和摩擦板产生纵向相互作用,端刺纵向刚度为线性,摩擦板与底座板的摩擦阻力为非线性。
6)桥梁固定支座可完全阻止梁的伸缩,活动支座抵抗伸缩的阻力可忽略不计,不考虑支座本身的纵向变形。
7)桥梁墩台顶部纵向水平刚度为线性。
8)相邻股道钢轨、轨道板和底座板的纵向受力相互影响。
根据以上假定,建立如图2所示的轨—板—桥—墩空间一体化纵向力计算模型。
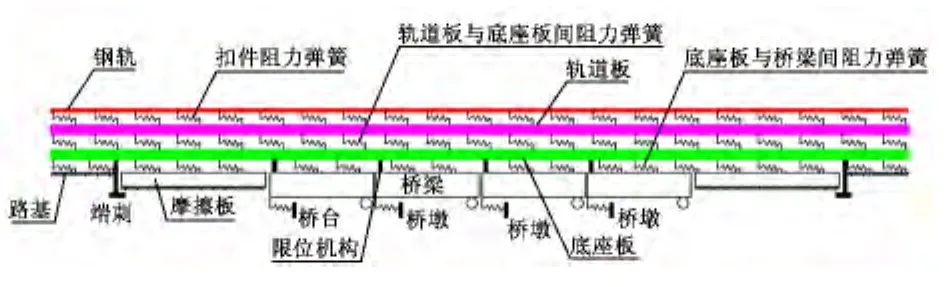
图2 轨—板—桥—墩纵向力计算模型
1.2 计算参数
计算参数主要包括钢轨、扣件、轨道板、底座板和“两布一膜”滑动层等结构的参数选取。
1)钢轨为60 kg/m轨,截面积为77.45 cm2,弹性模量为2.1×1011Pa,线膨胀系数为11.8×10-6。
2)扣件竖向刚度取60 000 kN/m;扣件纵向阻力r采用非线性弹簧模拟,有载r=60 kN/(m·线);无载r=30 kN/(m·线),极限位移u0=0.5 mm,如图3所示。
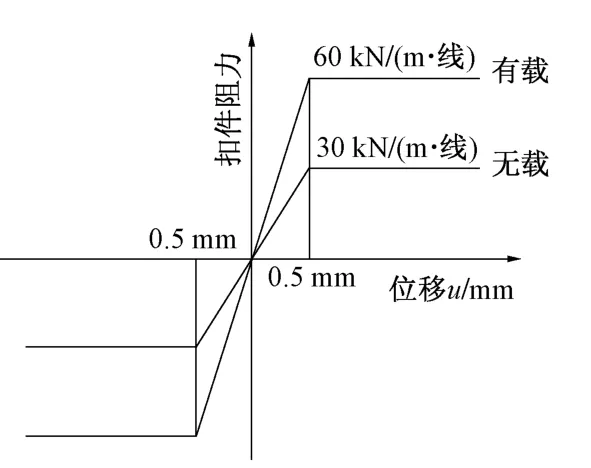
图3 扣件纵向阻力
3)轨道板宽度为2.55 m,厚度为0.2 m,混凝土弹性模量3.6×104MPa;底座板宽度为2.95 m,厚度为0.19 m,混凝土弹性模量3.4×104MPa。
4)底座板与桥梁之间“两布一膜”采用非线性弹簧模拟,竖向只受压不受拉,竖向刚度1.0×108kN/m,纵向摩擦系数取0.3,滑动极限位移0.5 mm。台后摩擦板与桥梁之间“两布一膜”隔离层采用非线性弹簧模拟,竖向只受压不受拉,竖向刚度1.0×108kN/m,纵向摩擦系数取0.7,滑动极限位移5 mm。
5)桥梁截面面积为8.962 m2,竖向抗弯惯性矩为11.0 m4,横向抗弯惯性矩为84.73 m4,混凝土弹性模量为3.55×104MPa。
结合现场实际工况,计算模型梁跨布置和桥墩纵向线刚度参数如表1所示。

表1 桥梁梁跨布置和桥墩纵向线刚度参数
1.3 梁轨相互作用受力变形分析
以梁体降温15℃工况为例,分析伸缩工况下桥梁—轨道系统的总体受力变形特征。从降温工况下梁体纵向位移曲线可以看出,各跨梁体位移曲线主要受自身温度跨度大小控制,温度跨度越大梁体的伸缩位移越大,32 m等跨度简支梁的位移曲线大致相同。
伸缩工况下轨道各结构层的总体位移特征如图4至图7所示。由位移特征图可以发现,轨道板和底座板的位移特征与钢轨相似。受连续梁温度跨度影响,连续梁上轨道结构伸缩位移与梁伸缩方向相同,最大位移量出现在连续梁与简支梁接缝附近,钢轨最大位移为0.43 mm,轨道板和底座板最大位移为0.45 mm,并且连续梁中部存在位移零点。桥梁最大位移出现在连续梁128 m温度跨度的滑动支座位置,位移量为18.33 mm。
钢轨相对于轨道板和底座板相对于梁面的位移分别如图8和图9所示。可以看出,梁体降温15℃时,大部分区域内梁面与底座板间的相对位移超过0.5 mm,最大为17.72 mm,即两者处于滑动状态;而轨道板和钢轨间的相对位移最大值为0.04 mm,远小于0.5 mm,扣件阻力处于弹性范围。
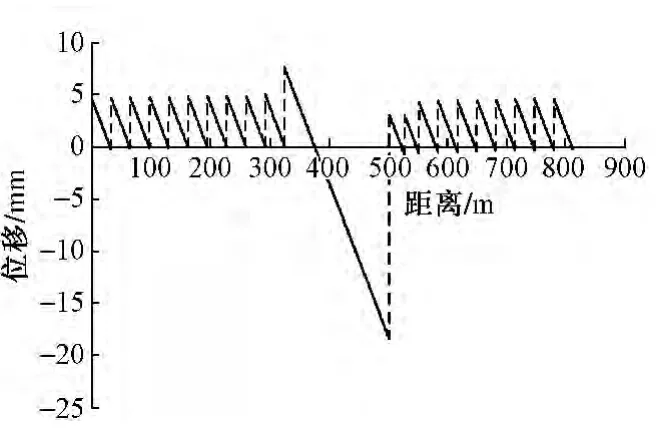
图4 桥梁位移
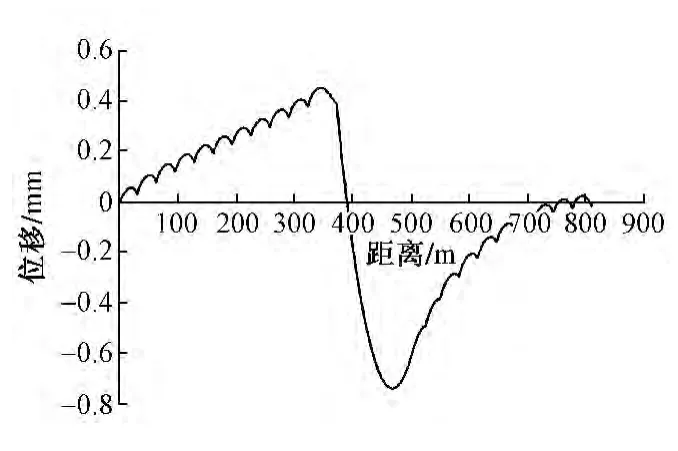
图5 底座板位移
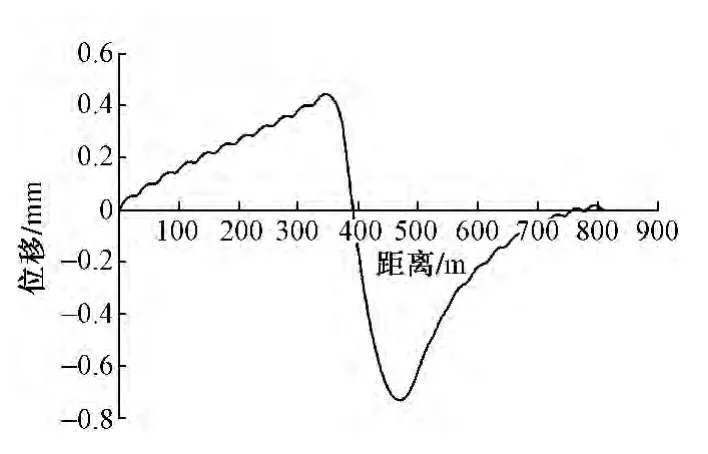
图6 轨道板位移
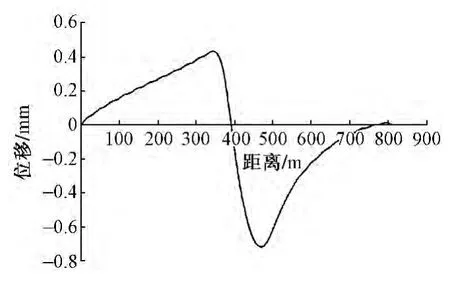
图7 钢轨位移
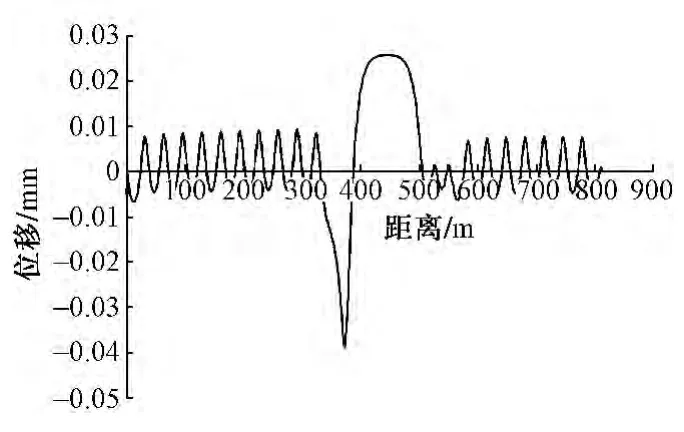
图8 钢轨相对于轨道板位移
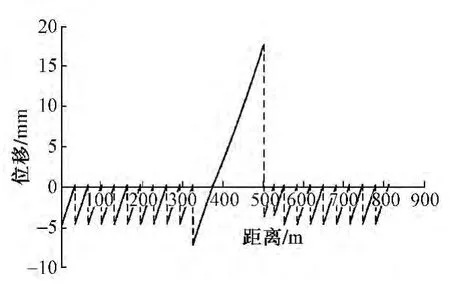
图9 底座板相对于梁面位移
伸缩工况下轨道各结构层的纵向力特征如图10~图12所示。由钢轨纵向力特征图可以看出,受中部连续梁较大温度跨度的影响,连续梁上钢轨受到较大压力,简支梁上部区域钢轨受拉。轨道板和底座板纵向受力特征与钢轨大致相同。连续梁固定支座上方附近区域轨道结构受到的伸缩附加力最大,钢轨、轨道板、底座板受到的最大伸缩附加力分别为28.4,295.1,580.1 kN。
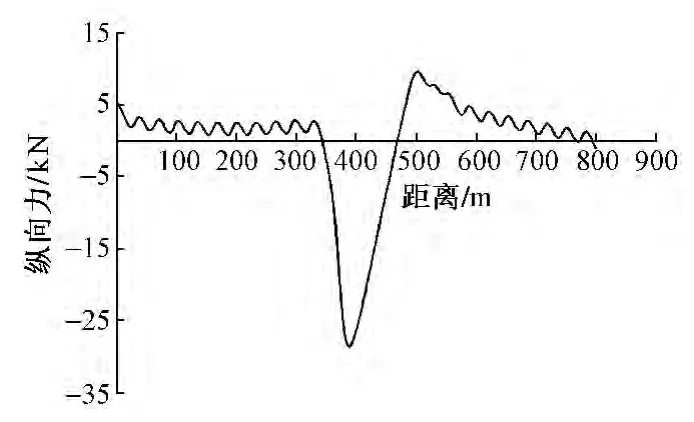
图10 钢轨纵向力
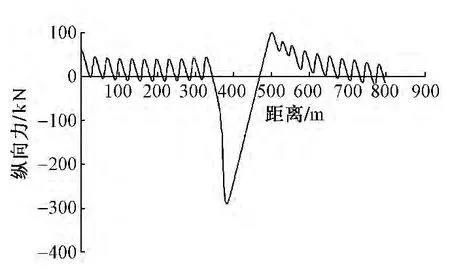
图11 轨道板纵向力
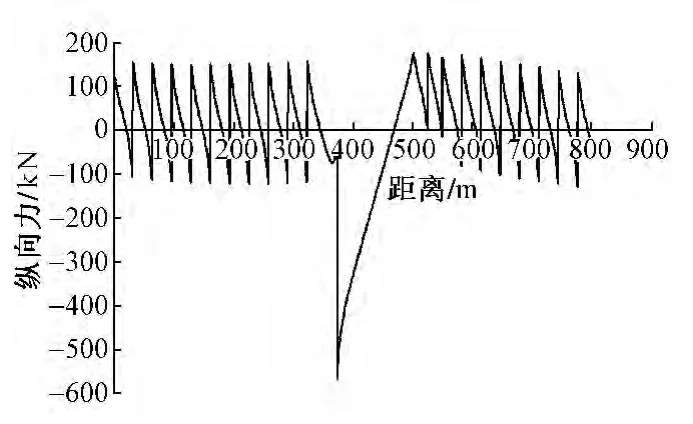
图12 底座板纵向力
剪力齿槽受力如图13所示。最大剪力出现在连续梁固定支座处,为591 kN。简支梁跨剪力齿槽受力主要与温度跨度大小有关,等跨的32 m简支梁上剪力齿槽受力较为均匀,在205~291 kN之间;而25 m和24 m跨度的简支梁上剪力齿槽受力为165 kN左右。桥墩承受的纵向力如图14所示。可以看出,连续梁固定支座所在的12号桥墩所受的纵向力最大,为225 kN。
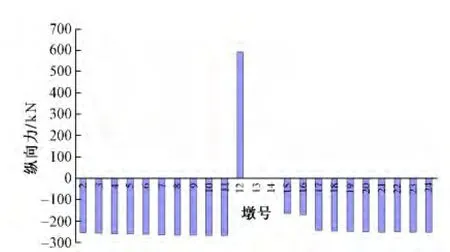
图13 剪力齿槽纵向力
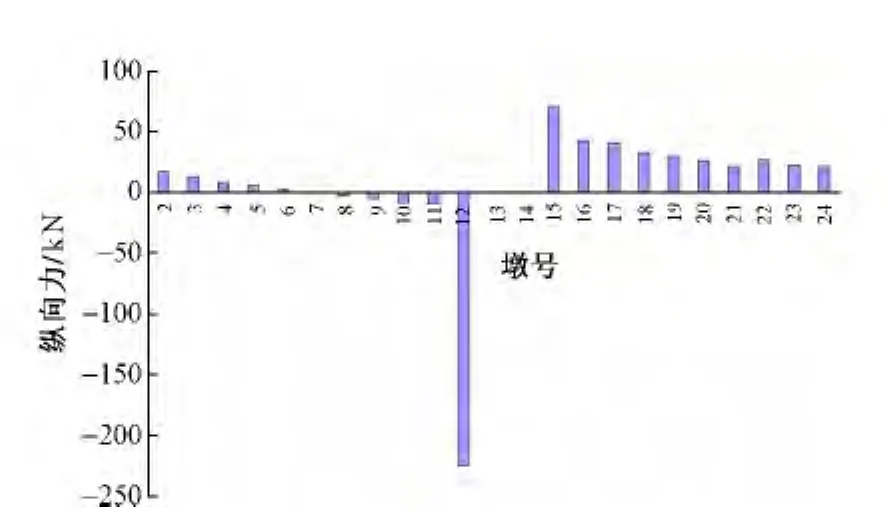
图14 桥墩纵向力
2 梁轨相互作用受力监测
梁轨相互作用受力监测以32 m简支梁和(48+80+48)m连续梁(温度跨度128 m)为主,监测时间为1年,对桥上CRTSⅡ型板式无砟轨道系统温度伸缩作用下桥梁与底座板的相对伸缩变形进行长期监测,轨道结构与梁体间相对位移如图15和图16所示。由监测结果可知:在-4℃ ~37℃的温度变化范围内,底座板与梁体间相对位移最大值分别为简支梁7.9 mm,连续梁30.4 mm,相对位移日变化量在3.0 mm以内,与理论计算结果相吻合。桥上CRTSⅡ型板式无砟轨道结构“两布一膜”滑动层有较好的滑动性能,能起到减少梁轨间相互作用力的效果。

图15 简支梁轨道结构与梁体间位移变化
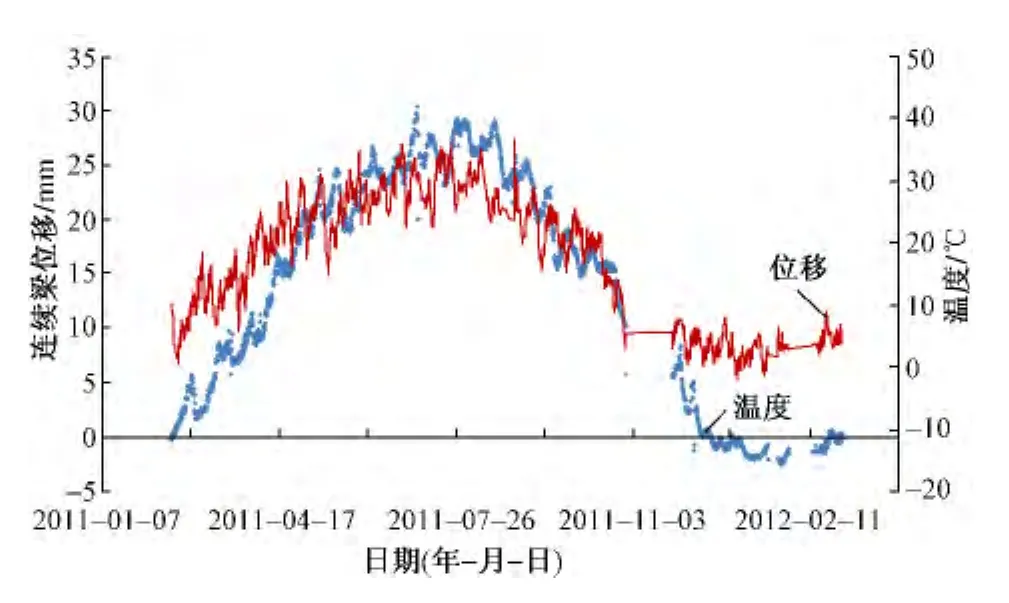
图16 连续梁轨道结构与梁体间位移变化
3 结语
针对高速铁路桥上CRTSⅡ型板式无砟轨道在温度伸缩作用下梁轨相互作用的受力变形特征,在理论计算分析的基础上,首次进行了32 m简支梁和大跨连续梁上的梁轨相互作用下桥梁和轨道结构的受力变形特征长期监测,得到如下结论:
1)梁轨相互作用理论计算中,当梁体降温15℃时,梁面与底座板间的相对位移超过0.5 mm,最大相对位移为17.72 mm,出现在连续梁128 m温度跨度的滑动支座位置,即两者处于滑动状态;而轨道板和钢轨间的相对位移最大值为0.04 mm,远小于0.5 mm,扣件阻力处于弹性范围。在连续梁固定支座上方附近区域,轨道结构受到的伸缩附加力最大,钢轨、轨道板、底座板受到的最大伸缩附加力分别为28.4,295.1,580.1 kN,连续梁固定支座处剪力最大,为591 kN。
2)在监测的1年里,温度变化范围为 -4℃ ~37℃,32 m简支梁的桥梁—轨道最大相对位移7.9 mm,(48+80+48)m连续梁的桥梁—轨道最大相对位移为30.4 mm,相对位移日变化量在3.0 mm以内,与理论计算结果相吻合。桥上CRTSⅡ型板式无砟轨道系统中“两布一膜”滑动层起到了较好的滑动作用。
3)由于高速铁路线路运营时间较短,应对桥上CRTSⅡ型板式无砟轨道系统中较为关键的梁轨相互作用继续进行监测,进一步掌握桥梁—轨道的受力变形特征。
[1]雷晓燕,圣小珍.现代轨道理论研究[M].北京:中国铁道出版社,2008.
[2]安国栋.高速铁路无砟轨道技术标准与质量控制[M].北京:中国铁道出版社,2009.
[3]田利民.客运专线无砟轨道系统设计[J].中国铁道科学,2008,29(1):13-16
[4]王继军,尤瑞林,王梦,等.单元板式无砟轨道结构轨道板温度翘曲变形研究[J].中国铁道科学,2010,31(3):9-14.
[5]徐庆元,张旭久,曾志平.无砟轨道纵向连接形式对列车—板式无砟轨道—路基系统振动特性影响[J].中国铁道科学,2010,31(1):32-37.
[6]铁道部工程管理中心.京津城际轨道交通工程CRTSⅡ型板式无砟轨道技术总结报告[R].北京:铁道部工程管理中心,2008.
[7]中国铁道科学研究院铁道建筑研究所.CRTSⅡ型板式无砟轨道结构与桥梁间相互作用试验研究报告[R].北京:中国铁道科学研究院铁道建筑研究所,2011.

