一种在扩散加权图像降噪中的算法
易三莉 贺建峰 邵党国 刘正刚
(1.云南昆明理工大学信息工程与自动化学院,昆明,650500;2.云南昆明理工大学外国语言文化学院,昆明,650500)
引 言
扩散张量成像(Diffusion tensor imaging,DTI)技术的出现是医学影像技术领域中一个非常大的进展,它实现了对脑白质纤维的无创成像。DTI是根据Stejskal-Tanner方程对扩散加权图像(Diffusion weighted imaging,DWI)的计算 得来[1,2]。由于大脑内部具有丰富的白质结构,因而决定了扩散张量图像具有多边界的特点,并且DWI图像中的边界信息对于大脑白质结构的反映尤其重要。因而要求对扩散张量图像进行降噪的同时,能较好地保存图像的边界信息。针对DWI图像多边界,数据量大,低信噪比且噪声为莱斯分布的特点,国内外研究人员提出了许多对DWI进行降噪的算法。如McGraw[3]等应用全变差(Total variation,TV)滤波方法进行扩散张量图像的降噪,Basu[4]等将基于贝叶斯理论的最大后验估计滤波器对扩散张量图像进降噪,以及Fernandez[5]等人采用了各向异性维纳滤波的方法,国内张相芬[6]等人应用向量复扩散模型对DWI图像进行降噪等。
自适应维纳滤波器是一种经典的线性降噪滤波器,其抗噪性能优良并且计算简单。然而,由于DWI图像具有丰富的边界信息,且其噪声分布为莱斯噪声,直接将自适应维纳滤波方法应用于对DWI图像的降噪并不能取得较好的效果。这是因为:首先,DWI图像的噪声主要集中于图像的高频部分,图像的低频部分含有的噪声较高频部分而言则要小很多。自适应维纳滤波算法在对图像进行降噪的过程中,并不能分辨图像中的不同频率成份,因而只能对所有频率成份都不加区分地进行滤波降噪处理。二维经验模态分解算法则可将图像分解为表示不同频率成份的细节图像以及轮廓图像,它是一种将Hilbert-Huang变换用于图像等二维信号处理的方法[7]。其次,自适应维纳滤波器主要针对高斯噪声具有较好的抗噪性能,对于莱斯噪声则并不十分理想。通过使用改进的维纳滤波算法能够使其更适用于对DWI图像的降噪。本文提出了一种将二维经验模态分解(Bidimensional empivical mode decomposition,BEMD)和改进的维纳滤波器相结合的算法,并将该算法应用于DWI图像的降噪。
1 BEMD与改进的维纳滤波法算法
1.1 二维经验模态分解
二维经验模态分解是在一维经验模态分解的基础上发展而来的。一维经验模态分解算法(Empirical mode decomposition,EMD),最 初 是 由Huang等人于1998年提出的用于对复杂信号进行平稳化处理的信号处理方法[8]。它首先对一个时间序列进行经验模态分解,将信号分解为有限个内禀模式函数(Intrinsic mode function,IMF),然后对各个分量IMF做希尔伯特变换从而得到其瞬时频率与振幅。从本质上来看,该方法的处理结果是将信号中不同尺度的波动或趋势逐级分解开来。由于这种分解是基于局部特征尺度,因而它具有良好的局部自适应性及多尺度的优点。由于EMD在一维信号的处理尤其是非平稳信号的处理上具有较好的效果并得到广泛的应用,近年来一些国内外研究者将其推广到二维图像分析并且取得了一定的成果。如瑞典的Linderhed[9]在2005年提出了基于样条插值的二维EMD方法,并将该方法用在图像压缩中;Damerval[10]提出了基于三角剖分和立方样条插值的二维EMD,将它用于图像降噪并取得较好的效果;Nunes[11]等人基于数学形态学重构进行图像的BEMD分解,并将其用于纹理图像及医学图像的分析。国内葛光涛[12]等通过对BEMD算法引入新的筛分停止准则实现更好的保留图像细节。
对于二维图像,采用BEMD进行分解必须基于以下假设[13]:(1)二维数据平面至少包含一个极大值点和一个极小值点,或整个二维平面没有极值点,但在进行一阶或多阶求导运算后能出现一个极大值点和一个极小值点;(2)特征尺度用极值点之间距离定义。
对一幅图像f(x,y)进行二维经验模态分解,将它分解为有限个二维IMF以及最终的余项函数。其分解方法与一维处理基本相同,所得到的二维IMF具有如下特征:IMF的极值点数目等于过零点的数目,或者最多相差为1;IMF的局部极大值所构成的上包络面与局部极小值所构成的下包络面的均值曲面为零。BEMD算法的具体实现如下:
(1)赋初值,令i=1,k=1,分别表示第i个IMF以及为了计算IMFi所进行的第k次循环,余项的初值为:rik(x,y)=f(x,y)。
(2)计算rik(x,y)的极大值包络hup(x,y)以及它的极小值包络hlow(x,y)。
(3)计算rik(x,y)的均值曲面:mean(x,y)= (hup(x,y)+hlow(x,y))/2。
(4) 根 据rik(x,y) 以 及 它 的 均 值 曲 面mean(x,y) 计 算 其 差 值 函 数:Dik(x,y) =rik(x,y)-mean(x,y)。
(5)对差值函数Dik(x,y)进行判断,看它是否满足上文所述IMF函数的特征:当它满足时,就可得到内禀模式函数:IMFi(x,y)=Dik(x,y),令r(i+1)1(x,y)=ri1(x,y)-IMFi(x,y),并且令i=i+1,k=1,重复(2)~(4)计算下一个内禀模式函数;当不满足时,令ri(k+1)(x,y)=Dik(x,y),并且令k=k+1,重复(2)~(4)直到差值函数满足内禀模式函数为止。
综上所述,对于图像f(x,y)通过BEMD分解为n个内禀模式函数IMFi及其余项函数r(x,y)可以用下式来表示
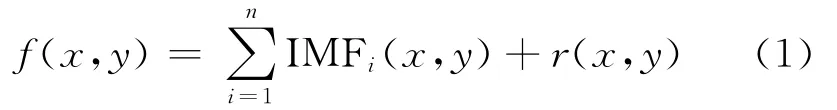
通过BEMD算法可将图像分解为一系列细节信息和趋势信息。上式中的内禀模式函数IMFi即表示图像的细节信息,对应图像中的边缘、噪声等高频信息,i的值越小表示越早分解出来的内禀模式函数,它所含有的频率也就越高,余项函数r(x,y)则表示了图像的基本结构、基本变化的趋势信息[8]。
1.2 改进的自适应维纳滤波

由于扩散加权图像中的噪声为莱斯噪声,而维纳滤波器是针对高斯噪声进行降噪的,直接用维纳滤波器对扩散加权图像进行降噪并不能得到理想的降噪效果[14]。莱斯校正技术在核磁共振图像中应用较为广泛,对于含有莱斯噪声的信号,当信噪比较高时它趋向于高斯分布,因此可以在对扩散加权图像进行降噪之前先通过莱斯校正技术对扩散加权图像中的数据进行校正处理,从而使处理后的图像可运用维纳滤波算法对其进行降噪处理。
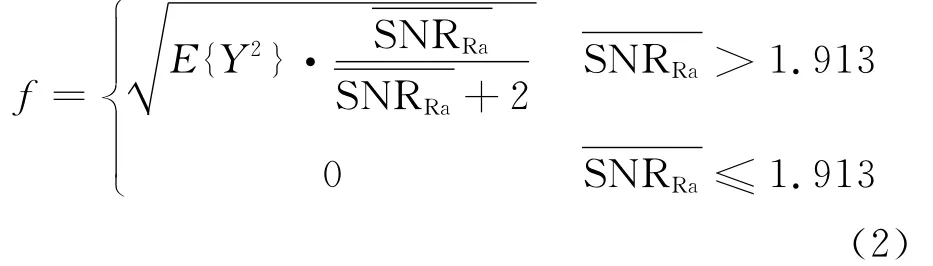
通过式(2)进行莱斯校正之后所得到的图像f则可通过自适应维纳滤波器对其进行降噪处理。对于图像f(x,y)(其中(x,y)表示像素点f(x,y)在图像中的位置),自适应维纳滤波器就是寻找图像的估计值(x,y)满足它与图像f(x,y)之间的均方误差为最小。因而自适应维纳滤波器对该图像的降噪模型表示如下
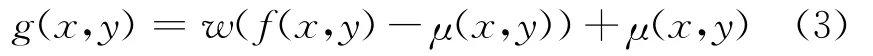
式中:g(x,y)是滤波结果,μ(x,y)为图像邻域均值,w是自适应维纳滤波器,其表达式为
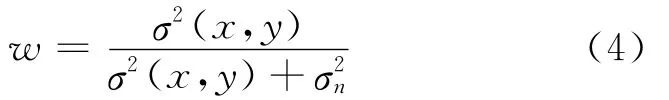
1.3 BEMD与维纳滤波的结合算法
由于DWI图像是由不同的频率成份组成的,图像的高频成份代表着图像的细节信息,而图像的低频成份代表图像的趋势信息。对于一幅含噪的DWI图像,其噪声主要集中于它的高频部分,而图像的低频部分含有的噪声较高频部分而言则要小很多。事实上,由于自适应维纳滤波算法对图像中所有频率成份都不加区分地进行滤波降噪处理并不合理。对于图像中不含噪或者含噪非常少的图像成份而言,不仅不能改善图像质量,反而由于滤波器的过滤波作用使图像质量变差。本文通过将二维经验模态分解和改进的自适应维纳滤波相结合的方法对DWI图像进行降噪处理。
首先,使用上文所述的BEMD算法,将含噪图像分解为四个不同频率成份的子图像IMF1,IMF2,IMF3及REF。它们分别对应的频率成份为从高到低:IMF1体现了原始含噪图像的高频信号部分,主要反映图像的边界等细节;第2个分量IMF2所包含高频成份较分量IMF1次之,但仍然具有丰富的边界信息;第3个分量IMF3则包含较多的低频成份;图像的余项部分即REF则体现了图像中的低频成份,代表图像趋势信息。
然后采用改进的自适应维纳滤波器对不同子图像进行处理。事实上,由于噪声主要集中于图像中的高频部分,因而对IMF1和IMF2采用改进的自适应维纳滤波算法进行降噪,从而得到更准确的边界信息。而对于IMF3和REF,它们主要体现的是图像的趋势信息,因而保持原始图像不变。
最后,将处理后的对应各频率成份子图像进行相加得到降噪后的图像。
2 实验结果与分析
将本文所提出的BEMD与改进的维纳滤波器相结合的算法用于DWI图像的降噪,来对该算法的降噪性能进行分析比较。实验中采用GE1.5T磁共振系统对人脑进行DWI成像,扫描参数为:TR=12 000ms,TE=107ms,图像大小为256×256,体素大小为1mm×1mm×4mm,梯度编码方向数为13,b=1 000s/mm2,其参考DWI图像为DWI0每一层DWI数据集中包括一幅未加权的参考图像DWI0,以及13幅扩散加权的图像DWI1~13,共计14幅DWI图像。本文通过对编码方向为0的图像DWI0进行相关的实验分析。
2.1 DWI图像的BEMD分析
使用BEMD方法将DWI图像分解为3个IMF图像及一个余项函数图像,共计4个子图像。分解后的结果如图1所示,其中图1(a~e)分别表示DWI0,IMF1,IMF2,IMF3以及余项函数。从图1可以看到,IMF1几乎包含了图像的的所有细节信息,而IMF2所含的细节信息较IMF1要少,IMF3则包含更少的细节信息,而在余项图像中几乎看不到图像的细节信息而只是图像的趋势信息。
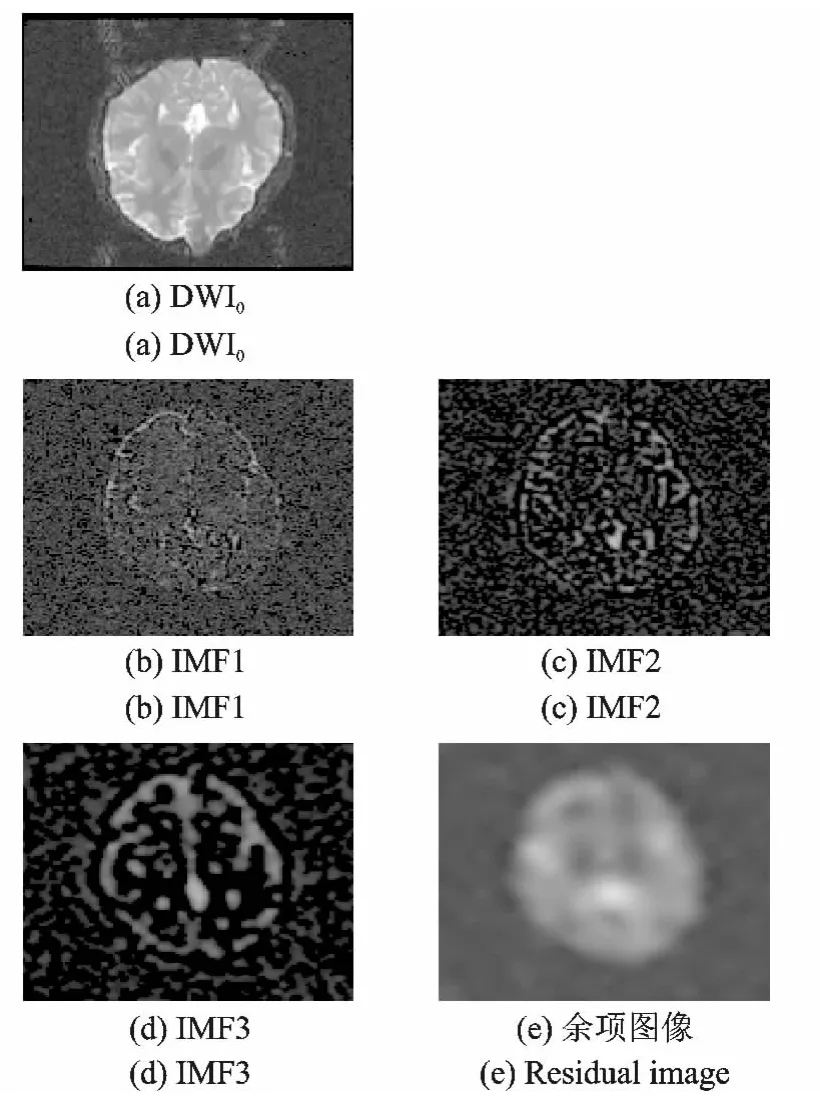
图1 DWI0及BEMD算法对其分解结果Fig.1 Decomposed results of DWI0of BEMD method
2.2 降噪效果比较
通过两个实验来对本文所提出的降噪算法进行分析比较。
首先,在第一个实验中,将莱斯噪声加入到原始DWI图像中,莱斯噪声的大小设置为:σ2Ra=0.05:0.05:0.25(其中σ2Ra为莱斯噪声的方差),然后将自适应维纳滤波方法、改进的维纳滤波法以及本文所提出的基于BEMD算法的滤波方法分别应用于含噪的DWI图像的降噪中,其结果如表1所示。从表1中可以看到与BEMD相结合的算法相较于其他算法,随着信噪比的增加,具有更高的峰值信噪比(Peak signal to noise ratio,PSNR),从而其降噪性能更好。
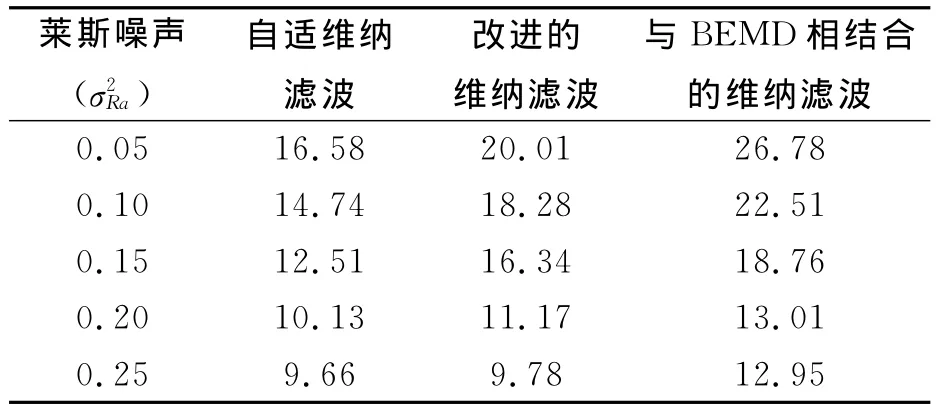
表1 降噪结果的PSNR比较Table 1 PSNR of denoising results of different methods
其次,在第二个实验中,将方差σ2Ra=0.1的莱斯噪声加入到原始的DWI0图像中,并将上述三种算法应用于对该含噪DWI图像的降噪。降噪结果如图2所示,其中图2(a)为含噪的DWI图像,图2(b)为自应用维纳降噪图像;图2(c)为使用改进的维纳滤波进行降噪的图像;图2(d)为使用本文所提出的BEMD与改进的维纳滤波相结合的算法所得到的降噪图像。

图2 不同降噪算法对含噪DWI0图像的降噪Fig.2 Denoised results of DWI0of different denoising methods
从图2中,可以看出图2(d)的降噪效果最为理想,即BEMD与改进的维纳滤波器相结合的算法降噪后所得到的图像最接近原始图像。因此,可得出与上个实验相同的结论,即本文所提出的算法能够更好地对DWI图像进行降处理。
3 结束语
本文针对DWI图像的特点,提出了BEMD和改进的维纳滤波器相结合的降噪算法,并将该算法应用于DWI图像的降噪中。通过采用BEMD算法将具有丰富边界信息的DWI图像分解为含有不同频率成份的内禀模式函数IMF,得到分别代表图像高频成份以及代表图像低频成份的子图像;根据噪声主要集中于图像高频部分的特点,采用改进的维纳滤波算法对不同子图像进行不同的降噪处理;最后将处理后的子图像相加得到最终的降噪图像。在本文的实验中,将该算法应用于DWI图像的降噪中,并将其与维纳滤波器的降噪结果进行比较。通过比较,可以看出本文算法具有更峰值信噪比,即本文所提方法较维纳滤波算法具有更好的降噪效果。
[1]Basser P J,Mattiello J,LeBihan D.MR diffusion tensor spectroscopy and imaging[J].Biological Physics,1994,66:259-267.
[2]Stejskal E O,Tanner J E.Spin diffusion measurements:spin echoes in the presence of a time-dependent field gradient[J].Journal of Chemical Physics,1965,42:288-292.
[3]McGraw T,Vermuri B C,Chen Y,et al.DT-MRI denoising and neuronal fiber tracking [J].Medical Image Analysis,2004,8:95-111.
[4]Saurav B,Thomas F,Ross W,Rician noise removal in diffusion tensor MR[J].MICCAI,LNCS4190,2006:117-125.
[5]Martin-Fernandez M,Munoz-Moreno E,Cammoun L,et al.Sequential anisotropic multichannel Wiener filtering with Rician bias correction applied to 3Dregularization of DWI data[J].Medical Image Analysis,2009,13:19-35.
[6]张相芬,田蔚风,叶宏.DTI图像恢复的向量复扩散模型[J].计算机工程与设计,2009,30(3):634-635.
Zhang Xiangfen,Tian Weifeng,Ye Hong.Restoring DTI images by vector-valued complex diffusion model[J].Computer Engineering and Design,2009,30(3):634-635.
[7]Nunes J C,Bouaoune Y,Delechelle E,et al.Image analysis by bidimensional empirical mode decomposi-tion[J].Image and Vision computing,2003,21:1019-1026.
[8]Huang N E,Shen Z,Long S,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc R Soc Lond Ser A,1998,454:903-905.
[9]Linderhed A.Compression by image empirical mode decomposition[C]∥Image Processing,IEEE International Conference on Image Processing.Piscataway,USA:IEEE,2005:553-556.
[10]Damerval C,Sylvain M,Valerie P.A fast algorithm for bidimensional EMD [J].Signal Processing Letters,IEEE,2005,12(10):701-704.
[11]Nunes J C,Bouaoune Y,Delechelle E.Image analysis by bidi-mensional empirical mode decomposition[J].Image and Vision Computing,2003,21(12):1019-1026.
[12]葛光涛,桑恩方,刘卓夫,等.一种新的BEMD筛分停止准则[J].数据采集与处理,2010,25(2):195-200.
Ge Guangtao,Sang Enfang,Liu Zhoufu,et al.Novel BEMD criterion for stopping sifting process[J].Journal of Data Acquisition and Processing,2010,25(2):195-200.
[13]周欣,李衷怡.基于二维经验模式分解的图像去噪[J].计算机与数字工程,2007,35(11):93-94.
Zhou Xin,Li Zhongyi.Image denoise based on BEMD method[J].Computer and Digital Engineering,2007,35(11):93-94.
[14]Martin M F,Westin C F,Alberola C L.3DBayesian regularization of diffusion tensor MRI using multivariate Gaussian Markov random fields[J].Lecture Notes in Computer Science,2004,3216:351-359.
[15]Matzner R.An SNR estimation algorithm for comoplex baseband signals using higher order statistics[J].Facta Universitatis(Nis),1993,6:41-52.
[16]Koay C G,Basser P J.Analytically exact correction scheme for signal extraction from noisy magnitude MR signals [J].Journal of Magnetic Resonance,2006,179:317-322.

