基于聚类和微粒群优化的基因选择方法
刘金勇 郑恩辉 陆慧娟
(1.中国计量学院机电工程学院,杭州,310018;2.中国计量学院信息科学学院,杭州,310018)
引 言
基因表达谱数据又叫做微阵列数据,它是利用基因芯片技术测得的高通量基因在不同生理阶段的表达数据值。其中“基因表达”是指细胞在声明过程中,把储存在DNA中的遗传信息经过转录和翻译,转变成具有生物活性的蛋白质分子。“基因表达水平”是指某个基因在一定时间内控制产生的蛋白质的量,它表明了细胞当前的生理状态[1,2]。通过合理的方法对这种高通量的基因表达数据进行分析,可以得到哪些基因之间存在调控关系、不同样本之间哪些基因的表达水平发生了变化、不同的生理阶段如何影响基因的活动。
基因选择是采用某种优化算法从基因表达谱数据的所有属性中选择出一个最具有疾病识别能力的基因子集的过程[3,4]。选择出的基因子集在肿瘤识别过程中发挥着至关重要的作用。基于基因信息排序的过滤法[5]和依赖具体分类器选取基因的缠绕法[6,7]是两种主要的基因选择方法。基于排序的过滤法如、信噪比[8]、信息增益[9,10]等具有简单快速的特点,但它们都是按照单个基因蕴含的分类信息多少为标准的,没有考虑基因之间的相互联系,而含有分类信息高的基因组合并不一定是最优的组合[11]。缠绕法与具体分类器(如支持向量机(Support vector machine,SVM),ELM 等)结合,将分类器预测正确率作为评价基因组合好坏的标准,这种方法可以找出最优的基因组合,同时最小化基因子集,但算法每次评价一个基因组合都要进行分类器训练,时间复杂度较高,而且选择出的基因子集在其他类型的分类器中的泛化能力不高。
粒子群优化算法是一种新兴的基于群体智能的启发式全局搜索算法,通过粒子间的竞争和协作以实现在复杂搜索空间中寻找全局最优点。本文中使用粒子群算法来进行特征选择,但是由于大多数PSO算法在应用的过程中,其初始化都是随机的,不能保证初始群体粒子的合理分布,在PSO搜索过程中,就容易出现大部分粒子均被相同的局部极值所限制时,导致当前的粒子群失去多样性,陷入局部最好解,出现“早熟现象”,最终影响最优解的搜索。为了解决这一缺陷,在PSO算法进行搜索之前,先对基因进行聚类,并对聚类结果进行初步选择,将被选中的簇的中心作为PSO的初始值,每个被选中的簇作为一个搜索空间,并利用ELM的分类精度作为特征选择的适应评价标准。
这种将基因聚类提取基因先验信息并耦合进PSO算法进行特征选择的思想,由于其初始化都是固定的,且符合数据本身特点,在很大程度上代表了本来的数据,这样就保证了初始群体粒子的合理分布,在PSO搜索过程中,不容易出现大部分粒子均被相同的局部极值所限制的情况,避免出现局部最好解,最终得到的解便是最优解,且限制搜索范围能够减少搜索的时间,减少时间复杂度。
1 相关知识点
1.1 熵与信息增益
令X为随机变量,X的不同取值xi,i=1,2,… 对应着不同的概率P(xi),i=1,2,… ,那么X的信息熵定义为
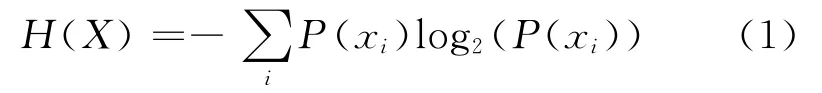
对于分类系统来说,类别C(c1,c2,…cl)是变量,因此分类系统的熵就可以定义为
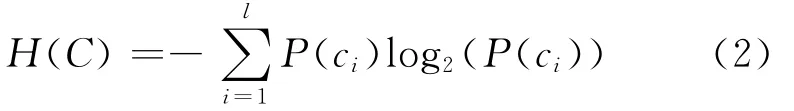
式(2)表示特征的变化越大,它所代表的信息也就越多。特别地,对于两类分类问题,信息熵可以表示为
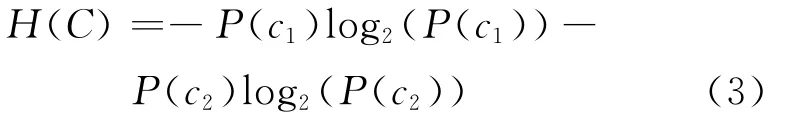
基因表达谱数据的信息增益是对每一个基因而言的,对应特定的含有n种情况的基因X,它所对应的条件熵为

其中P(ci|xj)代表基因xj属于类别ci的条件概率。该基因X为整个分类系统所带来的信息增益,可以用原系统的信息熵与基因X固定之后的条件熵之间的差值,用式(5)表示。
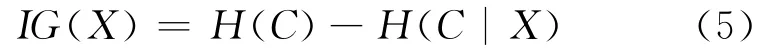
IG(X)便代表了基因表达谱数据中每个基因的信息增益,信息增益值越大,则该基因代表的分类信息就越多。
1.2 微粒群优化算法
PSO从这种模型中得到启示并用于解决优化问题。PSO中,每个优化问题的潜在解都是搜索空间中的一只鸟,称之为粒子。所有的粒子都有一个由被优化的函数决定的适值,每个粒子还有一个速度决定它们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个极值来更新自己;第一个就是粒子本身所找到的最优解,这个解称为个体极值;另一个极值是整个种群目前找到的最优解,这个极值是全局极值。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
假设在一个D维的目标搜索空间中,有N个粒子组成一个群落,其中第i个粒子表示为一个D维的向量
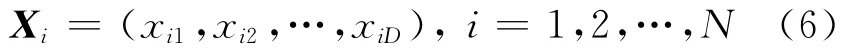
第i个粒子的“飞行 ”速度也是一个D维的向量
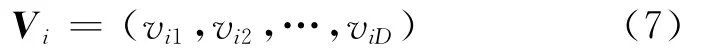
第i个粒子迄今为止搜索到的最优位置称为个体极值,记为

整个微粒群迄今止搜索到的最优位置为全局极值,记为
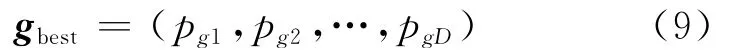
在找到这两个最优值时,粒子根据式(10,11)来更新自己的速度和位置
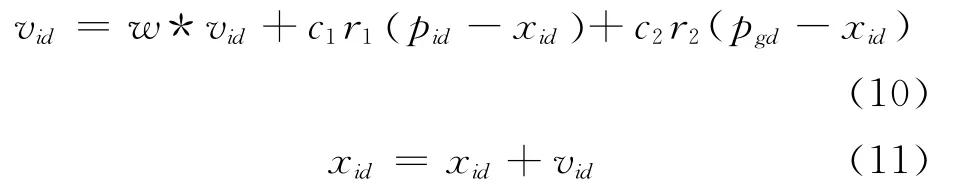
式中:c1和c2为学习因子,也称加速常数,r1和r2为[0,1]范围内的均匀随机数。式(6)右边由3部分组成,第1部分为“惯性”部分,反映了粒子的运动“习惯”,代表粒子有维持自己先前速度的趋势;第2部分为“认知”部分,反映了粒子对自身历史经验的记忆,代表粒子有向自身历史最佳位置逼近的趋势;第3部分为“社会”部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向群体或邻域历史最佳位置逼近的趋势,根据经验,通常c1=c2=2。vid是粒子的速度,vid∈[-vmax,vmax],vmax是常数,由用户设定用来限制粒子的速度。r1和r2是介于 [0,1]之间的随机数。
1.3 极限学习机
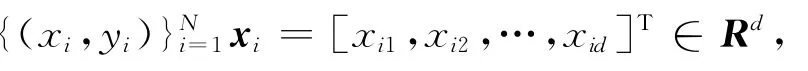
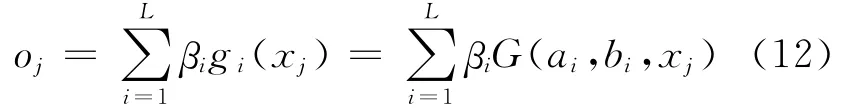
式中:βi为连接第i个隐层节点与输出神经元的输出权值,ai为连接输入神经元与第i个隐层节点的输入权值,bi为第i个隐层节点的偏置,oj为第j个输入样本的输出值,j=1,…,N。
如果含有L个隐层节点,且激活函数为g(x)的单隐层前馈神经网络可以零误差逼近于N个训练样本,即存在βi,ai和bi,使得
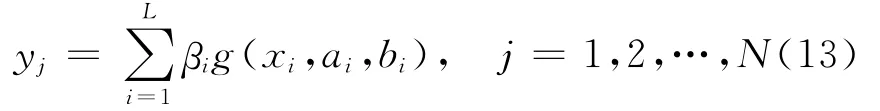
成立,并且

其中式(13)可以表示为

其中H称为ELM的隐层输出矩阵

如果隐层节点个数L和样本数量N是相等的,那么可以很容易的知道式(13,14)是成立的,但是当L<N时,单隐层前馈神经网络并不能零逼近于N个训练样本。这时式(15)可以表示为

E= [e1,e2,…,eN]T被称为是训练误差。这里训练一个ELM也即计算训练误差E的最小范数
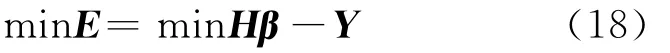
因此,通过式(18)并利用最小二乘的方法计算得到输出权重
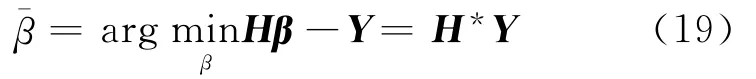
其中H*为矩阵H的Moore-Penrose广义逆。
2 基于聚类与PSO的基因选择
在基因组学中,聚类算法是研究基因间相互关系的最基本手段。聚类算法能够将那些具有相似功能特点的基因聚在一起,根据聚类的结果,可以预测未知基因的功能,寻找基因之间的调控关系以及发现共同的模式。其中比较流行的启发式方法是K-means方法。在对基因进行聚类时聚类数目的选择有两种方法,一种是随机选取,但是这种选取方法没有任何的针对性,需要迭代的次数较多,计算量也比较大;另外一种是根据某种准则选取,对基因表达谱数据的基因进行聚类时,需要结合数据本身的特点,包括数据的类别信息和冗余度信息等,如针对包含两种类别的样本进行聚类的时候,基因可以分为与样本类别相关的2簇以及1簇对样本分类无关的冗余基因,所以可以确定聚类数目为3。
将基因表达谱数据分成训练集和测试集,通过信息增益的方法选择前n个信息熵最大的基因。接下来便是利用聚类算法对初选的基因子集进行聚类,聚类方法采用K-means方法,聚类数目按照上述方法给出,如对于两类样本,聚类数目选择为3,k类样本则对应聚类数目为k+1。借助分类器对各簇的基因分类性能进行分析,将具有高分类性能的簇选择出来,排除对分类影响较小的簇,这些被选择的簇所包含的基因构成一个冗余度较低的特征基因子集。
最后将被选中的簇的中心作为初始位置,每一簇作为一个搜索空间,利用PSO进行Wrapper式的特征选择,本文采用ELM来评价基因优劣。根据ELM分类器返回的验证集上的准确率评价每个粒子的适应度值,通过不断更新PSO中群体粒子的位置和速度来搜索全局最优解。
对选取的基因的评价,利用ELM分类器计算PSO和聚类算法选择出来的特征基因的适应度,评价函数为
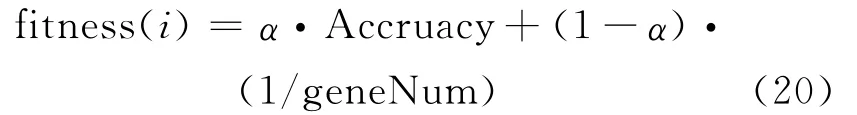
在特征选择过程中,应该选择样本测试精度高、基因个数少的粒子,即要选择适应度值最大的那个粒子,所选择的基因是依赖于ELM分类器的。在PSO中,一个粒子代表选择的一组基因子集,粒子在搜索过程中通过基因子集在分类器中评价,即PSO的适应值函数,更新个体最好位置和全局最好位置,直到达到最大迭代次数得到一组最优基因子集,最后利用分类器得到测试准确率,较好的即为提取到的关键基因。其中基因子集的评价函数的过程中,样本测试精度通过ELM分类器来完成的。选择出特征基因之后采用ELM建立分类模型,然后根据建立的模型测试分类正确率。
算法步骤描述如下:
(1)利用信息增益方法,对原始基因进行过滤,形成精简的基因子集FS;
(2)利用K均值聚类方法对FS进行聚类,将FS聚类为规定的簇数;
(3)使用ELM判断每一簇中基因的分类性能,并选择具有较高分类性能的簇中的基因作为特征基因子集FSC;
(4)将FSC的聚类中心作为PSO的初始化位置,每一个簇作为单独的搜索空间进行PSO搜索;
(5)对选取的基因的评价,如果满足要求的指标,则基因的选择过程结束,接下来进行步骤6;如果不满足要求,则采用式(10)和式(11)进行最优值和粒子位置和速度的更新,重新进行特征选择;
(6)选择出特征基因之后采用ELM建立分类模型,然后根据建立的模型测试分类正确率。
3 实验结果分析
为了验证算法的有效性,本文在3个基因表达数据集上进行仿真实验。白血病(Leukemia)、结肠癌(colon)、小圆蓝细胞(SRBCTs)。试验中用到的所有仿真都是在Matlab 2010a中实现的,所用计算机的配置为酷睿双核2.5GHz,2GB内存。由于基因表达谱数据的样本数非常少,所有的实验都采用K-折交叉验证的方法,其中k值均选择为5。
在开始特征选择算法之前,把数据集进行归一化处理,使得样本的每一维特征向量的均值为0,方差为1。接下来对基因表达谱数据使用信息增益的方法进行初步的选择,确定初选的基因子集,一般选择前200个信息增益值最大的基因构成候选基因子集。然后对这个子集进行k均值聚类,最佳的k值根据样本类别数而定,3个数据集分别为3,3和5。对基因表达谱数据的训练集的基因进行聚类后,将ELM作用于每个簇,得到该簇中最优基因子集的分类性能。图1~3分别为白血病、结肠癌和小圆蓝细胞数据集的每个聚类簇中不同数目的基因组合得到的最好分类精度。其中ELM分类器使用的激活函数为sigmoid函数,最优隐藏层节点数通过递增的方式从1增加到与训练样本数相等。
从图1~3中可以看出,随着选择基因数目的增多,分类正确率都基本呈现先增加后减少的趋势。在白血病数据集中单独使用簇1和簇3对样本进行分类获得的分类精度较簇3高;结肠癌数据集中簇2和簇3获得较簇1高的分类精度;小圆蓝细胞中簇1相较其他簇获得的分类精度比较低。所以根据2节中的描述,白血病数据集中簇2被视为冗余基因的集合,结肠癌数据集中簇1被视为冗余基因的集合,小圆蓝细胞中簇1被视为冗余基因的集合。
通过以上对基因聚类结果的分析,分别得到了3个数据集的备选特征基因子集。再用PSO结合ELM搜索最优基因子集。在搜索过程中PSO算法的种群规模设置为10,最大迭代次数为100,初始学习因子c1=2,c2=2,惯性权重w=0.8;ELM分类器使用sigmoid激活函数,最优隐藏层节点数通过递增的方式获得(从1增加到与训练样本数相等),适应度调节参数α设置为0.8。

图1 白血病数据不同簇中不同基因子集的分类性能Fig.1 The Leukemia dataset′s classification accuracy when sub-genes come from different clusters

图2 结肠癌数据不同簇中不同基因子集的分类性能Fig.2 The colon dataset′s classification accuracy when sub-genes come from different clusters

图3 小圆蓝细胞数据不同簇中不同基因子集分类性能Fig.3 The SRBCT dataset′s classification accuracy when sub-genes come from different clusters
当适应度值达到一定的阈值或者不在变化的时候,或者迭代达到最大次数时,搜索过程便结束。最大适应度值时对应的被搜索到的基因也就是该算法获得的最优关键基因。
适应度的设定是分类精度和被选择基因个数的综合指标,适应度值越高,说明分类精度越高,被选择的基因个数越少。分类精度越高则表明癌症的诊断率越高,被选择的基因个数越少表明获得的靶向基因越精确。
对使用本文方法选择后的样本进行分类,最优关键基因的个数和分类精度的结果在表1中给出。其中平均分类精度是30次结果的平均值。
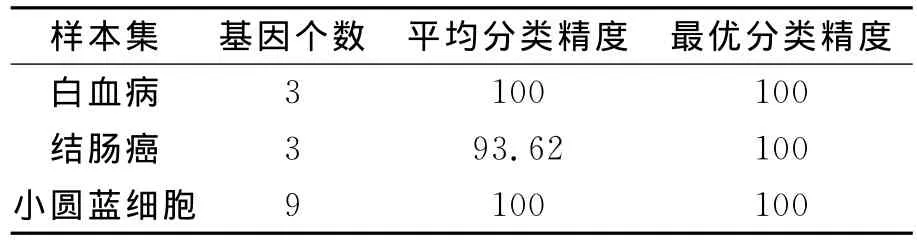
表1 关键基因个数与分类精度Table 1 Relationship between key genes′number and classification accuracy %
从分类结果可以看出使用该方法获得的关键基因子集能够获得非常高的分类精度,且能够尽可能多的消除冗余基因。在白血病数据集上,只需要3个关键基因,就可以获得100%的分类精度;在小圆蓝细胞数据集上只需要9个关键基因即可以获得100%的分类精度;在较难分类的结肠癌数据集上,只需要3个关键基因便可以获得93.62%的平均分类精度,但是在分类效果较好的时候能够获得100%的分类精度。3个数据集上的关键基因可以用表2描述。
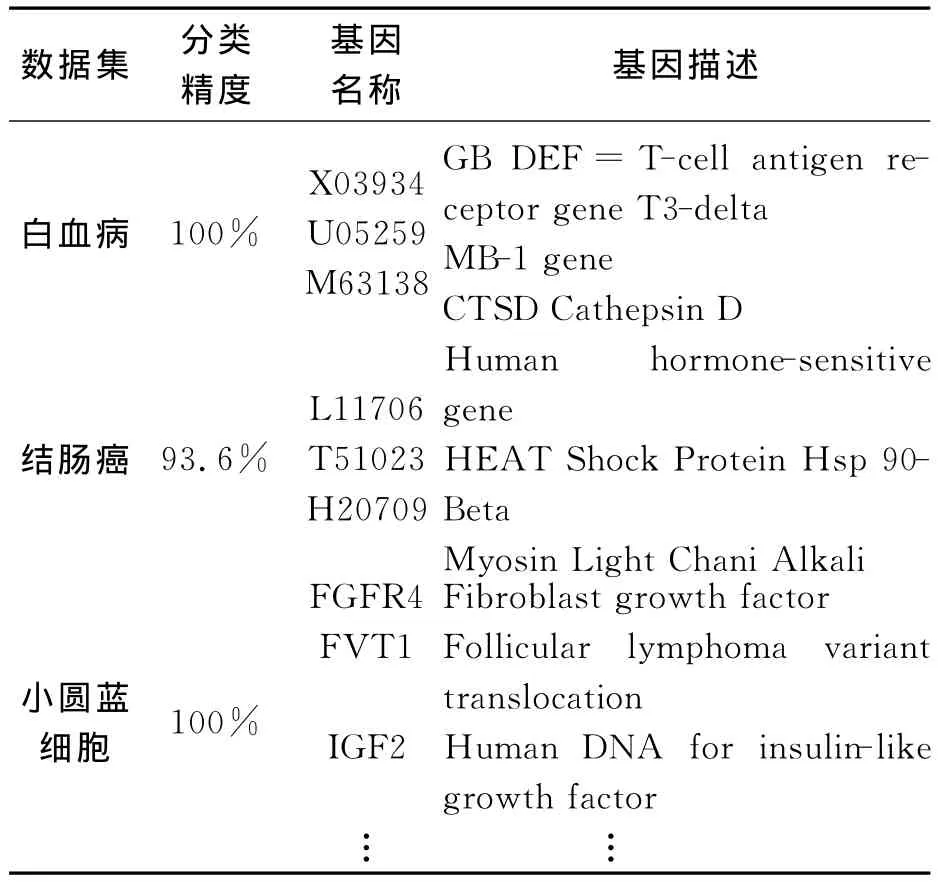
表2 本文方法选择的关键基因描述Table 2 Description of the genes selected by the proposed method
经查阅相关资料[2-3]可以发现,使用此方法获得的特征基因,确实是该基因表达谱数据对应的癌症的关键基因。因此该方法是具有很强的适用价值,不仅能够提高癌症的诊断率,而且能够有效获得靶向基因,为生物医学提供诊断的依据。
最后将本文所提方法与几种经典方法以及第3章中提出的PSO-Selection方法进行比较,包括分类精度和选择基因个数以及算法的耗时3个方面,比较结果见表3~5。
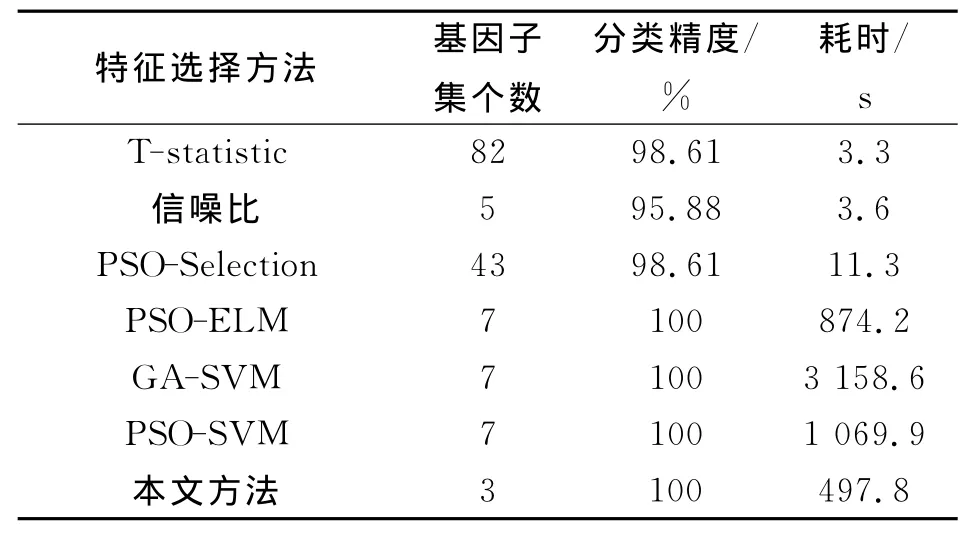
表3 本文方法与其他方法在白血病数据集上的比较Table 3 Comparison of the proposed method with other method on Leukemia dataset

表4 本文方法与其他方法在结肠癌数据集上的比较Table 4 Comparison of the proposed method with other method on SRBCT dataset
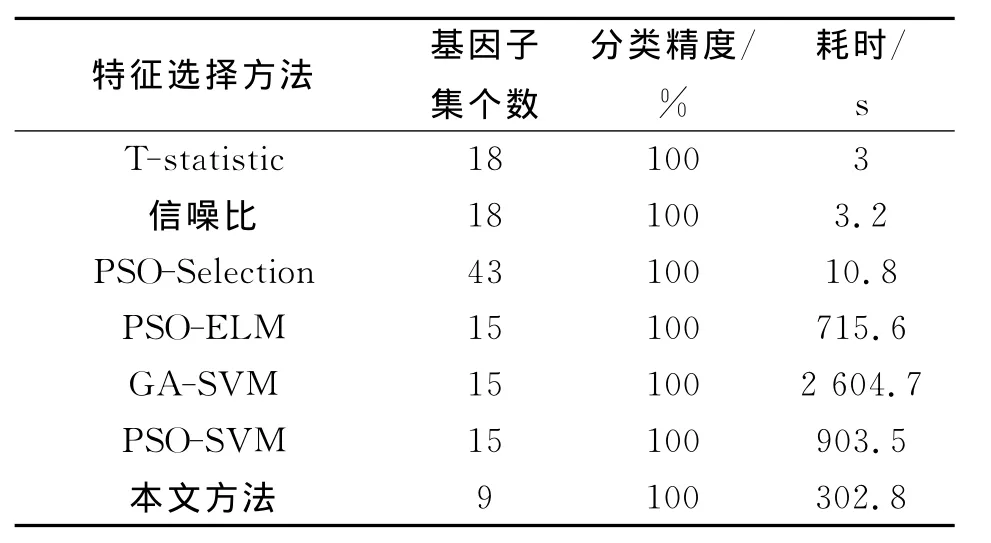
表5 本文方法与其他方法在小圆蓝细胞数据上的比较Table 5 Comparison of the proposed method with other method on colon dataset
从表3~5中可以看出,本文方法与其他6种方法相比,使用最少的基因子集便可以获得与经典的Wrapper方法近似的分类精度,在3个数据集上,白血病和小圆蓝细胞均获得100%的分类精度,在比较难分类的结肠癌数据集上获得的分类精度只比最优秀的特征选择方法低了0.03%。从算法的耗时上分析,可以看出本文方法虽然远高于T-statistic、信噪比和PSO-Selection方法,但是选择的基因子集个数比这3种方法少很多,且分类精度普遍高于这3种方法;而与PSO-ELM,GASVM,PSO-SVM 方法相比[15,16],在 基本上 没有降低分类精度的前提下,大大地降低了算法的耗时。虽然本文方法比PSO-ELM方法多了基因聚类以及聚类后簇的选择过程,但是在进行PSO搜索之前已经将搜索范围缩小,且使用聚类中心作为PSO的初始位置使得搜索过程更快趋于最优,这两个因素都使得本文方法的耗时远低于PSOELM方法。
4 结束语
为了有效降低基因表达谱数据基因之间的冗余度,本文提出了一种基于聚类和粒子群算法的基因选择方法。因为聚类算法可以根据基因的功能将具有相同功能的基因聚成一簇,不同功能的基因聚在不同的簇,通过合理的预处理,含有大量噪声的信息簇被移除,而具有高贡献度的基因簇的基因子集构成候选特征基因作为PSO的搜索空间。从实验结果可以看出,本文方法能够成功选择较少数目但是有较高分类率的基因子集。
[1]黄德双.基因表达谱数据挖掘方法研究[M].北京:科学出版社,2009.
Huang Deshuang.Research on data mining of gene expression[M].Beijing:Science Press,2009.
[2]郑继平.基因表达调控[M].合肥:中国科学技术出版社,2012.
Zheng Jiping.Regulation of gene expression[M].He fei:Chinese Science and Technology Press,2012.
[3]杨华.基于粒子群算法的特征选择方法研究[D].长沙:湖南大学,2010.
Yang Hua.Research on significant genes selection method based on PSO algorithm[D].Changshang:Hunan University,2010.
[4]Golub T R,Slonim D K,Tamayo P,et al.Class discovery and class prediction by gene expression monitoring[J].Science,1999,286:531-537.
[5]Liu H Q,Li J Y,Wong L.A comparative study on feature selection and classification methods using Gene expression profiles and proteomic patterns[J].Genome Informatics,2002,13:51-60.
[6]Zhao Z,Wang L,Liu H.Efficient spectral feature selection with minimum redundancy[C]∥Proceedings of the National Conference on Artificial Intelligence.Atlanta,Georgia,USA:[s.n.],2010,1:673-678.
[7]Chris D,PengH C.Minimum redundancy feature selection from microarray gene expression data [J]J Bioinform Comput Biol,2005,3(2):185-205.
[8]Hu Y,Loizou P C.Speech enhancement based on wavelet thresholding the multitaper Spectrum [J].IEEE Trans on Speech and Audio Processing,2004,12(1):59-67.
[9]刘庆和,梁正友.一种基于信息增益的特征优化选择方法[J].计算机工程与应用,2011,47(12):130-132.
Liu Qinghe,Liang Zhengyou.Optimized approach of feature selection based on information gain[J].Computer Engineering and Application,2011,47(12):130-132.
[10]任江涛,孙婧昊,黄焕宇.一种基于信息增益及遗传算法的特征选择算法[J].计算机科学,2006,10(33):193-196.
Ren Jiangtao,Sun Jinghao,Huang Huanyu.Feature selection based on information gain and GA [J].2006,10(33):193-196.
[11]Leung Y K,Hung Y.A multiple filter multiple wrapper approach to gene selection and microarray data classification[J].IEEE/ACM Transactions on Computational Biology and Bioinformatics,2010,7(1):108-117.
[12]Huang G B,Ding X J,Zhou H M.Optimization method based extreme learning machine for classification[J].Neurocomputing,2010,74:155-163.
[13]Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006(70):489-501.
[14]Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:a new learning scheme of feedforward neural networks[C]∥Proceedings of International Joint Conference on Neural Networks(DCNN2004).Budapest,Hungary:[s.n.],2004:25-29.
[15]陆慧娟.基于极限学习机集成的肿瘤基因表达数据分类[D].徐州:中国矿业大学,2013.
Lu Huijuan.Research on tumor gene expression data classification[D].Xuzhou:China Mining University,2013.
[16]郑馨,王勇,汪国有.EM聚类和SVM自动学习的白细胞图像分割算法[J].数据采集与处理,2013,28(5):614-619
Zheng Xin,Wang Yong,Wang Guoyou.White blood cell segmentation using expectation-maximization and automatic support vector machine learning[J].Journal of Data Acquisition and Processing,2013,5(28):614-619.

